Mathematics
Angle ABC = 60° and BA = BC = 8 cm. The mid points of BA and BC are M and N respectively. Draw and describe the locus of a point which is :
(i) Equidistant from BA and BC.
(ii) 4 cm from M
(iii) 4 cm from N
Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.
Answer
Steps of construction :
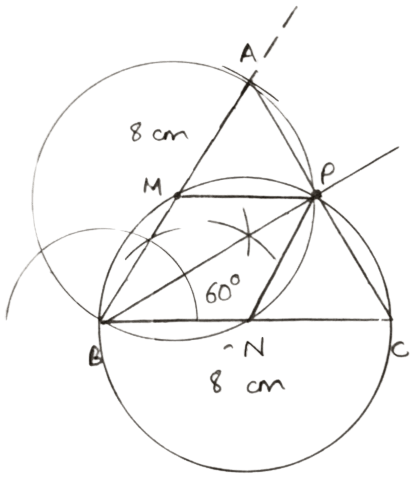
Draw BC = 8 cm.
Draw ∠XBC = 60°.
From XB, cut off AB = 8 cm. Join AC.
Mark mid-point of BA as M and BC as N.
Draw angle bisector of ∠ABC.
Taking center as M and radius = 4 cm draw a circle.
Taking center as N and radius = 4 cm draw a circle.
Mark point P as the intersection of circle with center M, N and angle bisector of ∠ABC.
Join MP and NP.
From figure,
BMPN is a rhombus.
(i) Hence, the locus of points equidistant from BA and BC is the bisector of ∠ABC.
(ii) Hence, the locus of point at a distance of 4 cm from M is the circumference of the circle with center M and radius = 4 cm.
(iii) Hence, the locus of point at a distance of 4 cm from N is the circumference of the circle with center N as radius = 4 cm.
Figure BMPN is a rhombus
Related Questions
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit the assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm, and ∠ABC = 60°.
(ii) Construct the locus of all points, inside △ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to △ABC.
(iv) Mark the point Q, in your construction, which would make △QBC equal in area to △ABC, and isosceles.
(v) Measure and record the length of CQ.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.
(i) Complete the rectangle ABCD such that :
(a) P is equidistant from AB and BC.
(b) P is equidistant from C and D.
(ii) Measure and record the length of AB.
Use ruler and compasses only for the following question. All construction lines and arcs must be clearly shown.
(i) Construct a △ABC in which BC = 6.5 cm, ∠ABC = 60° and AB = 5 cm.
(ii) Construct the locus of points at a distance of 3.5 cm from A.
(iii) Construct the locus of points equidistant from AC and BC.
(iv) Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.