Mathematics
If equal sides of an isosceles triangle are produced, prove that the exterior angles so formed are obtuse and equal.
Answer
In △ ABC,
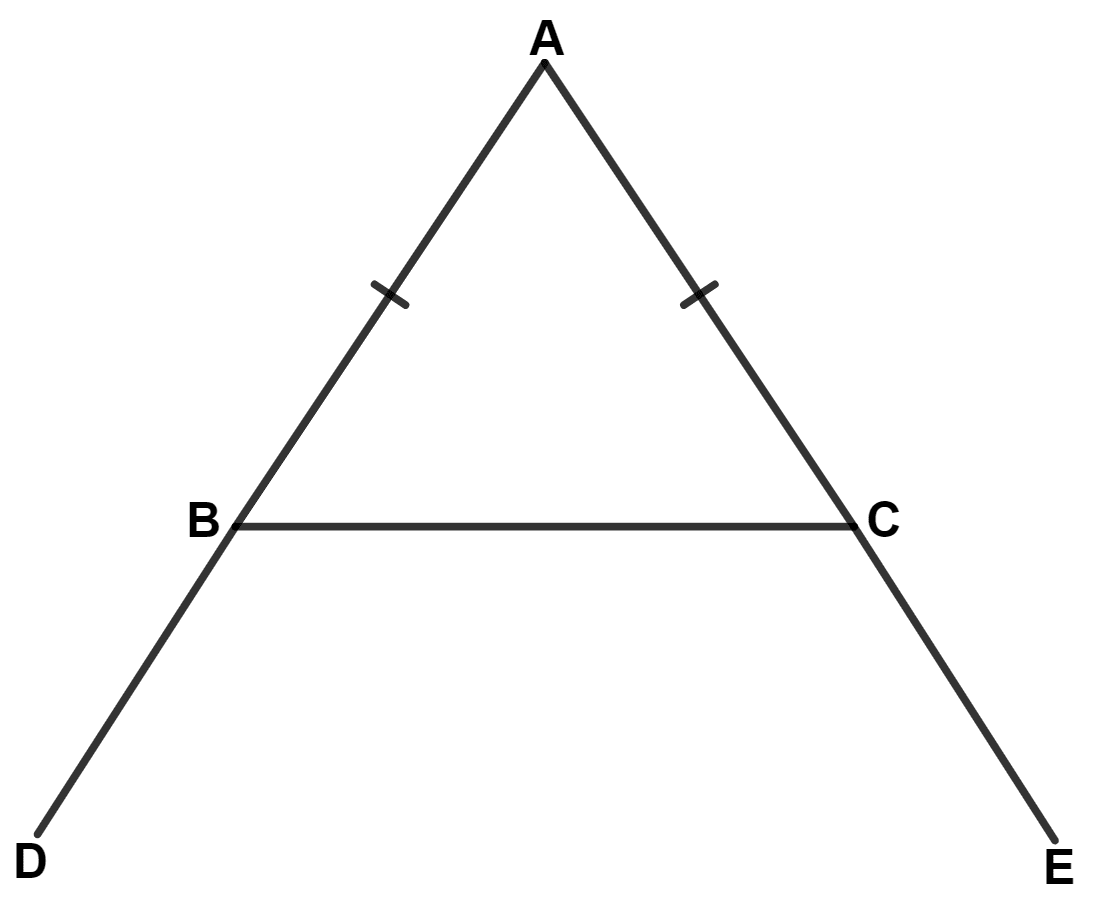
⇒ AB = AC (Given that triangle is isosceles)
⇒ ∠B = ∠C = x (let) [Angles opposite to equal sides are equal]
Since, ∠B = ∠C so they cannot be equal to or greater than 90° as, sum of all the three angles in a triangle is equal to 180°.
From figure,
ABD is a straight line.
∴ ∠ABC + ∠CBD = 180°
⇒ x + ∠CBD = 180°
⇒ ∠CBD = 180° - x ……….(1)
ACE is a straight line.
∴ ∠ACB + ∠BCE = 180°
⇒ x + ∠BCE = 180°
⇒ ∠BCE = 180° - x ……….(2)
Since, x is less than 90°.
∴ 180° - x > 90°.
From equation (1) and (2),
⇒ ∠CBD = ∠BCE and are obtuse angles.
Hence, proved that if equal sides of an isosceles triangle are produced, the exterior angles so formed are obtuse and equal.
Related Questions
In quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Given : ED = EC
Prove : AB + AD > BC.