Mathematics
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that : (i) Δ AMC ≅ Δ BMD (ii) ∠DBC is a right angle (iii) Δ DBC ≅ Δ ACB (iv) CM = 1/2 AB
Related Questions
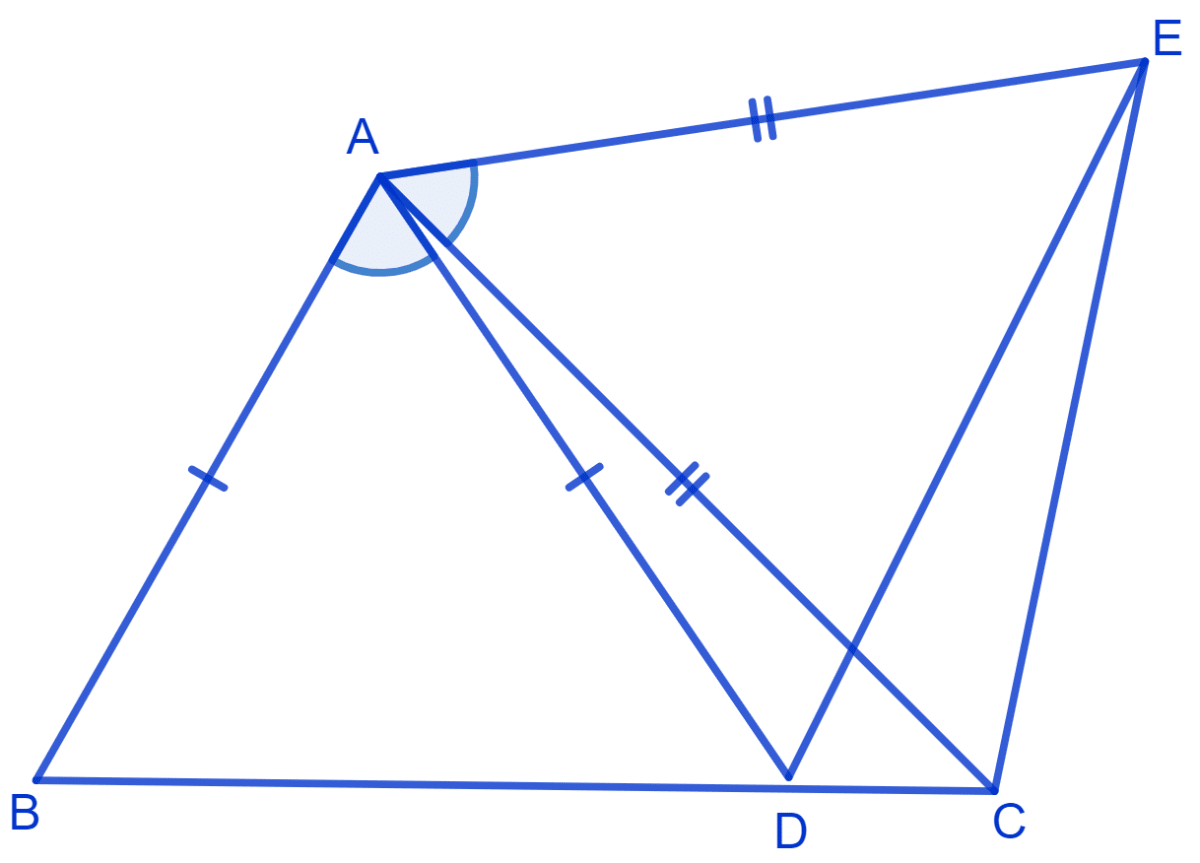
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
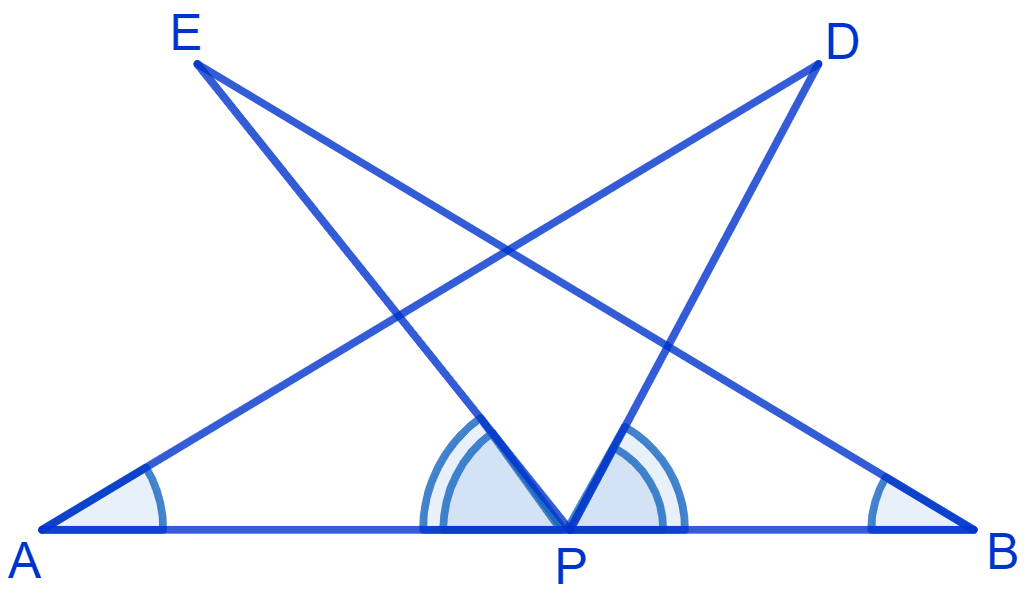
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that
(i) Δ DAP ≅ Δ EBP
(ii) AD = BE
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC
(ii) AO bisects ∠A
In Δ ABC, AD is the perpendicular bisector of BC. Show that Δ ABC is an isosceles triangle in which AB = AC.