Mathematics
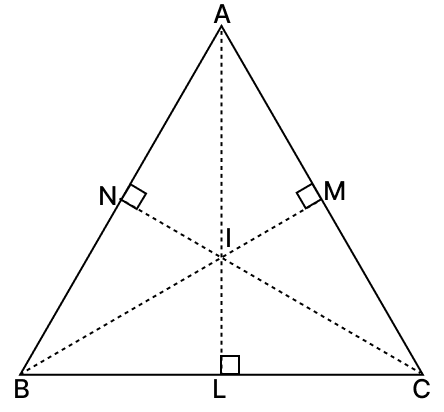
The perpendicular bisectors of the sides of a △ABC meet at I. Prove that : IA = IB = IC.
Answer
From figure,
AL, CN and BM are perpendicular bisectors of sides BC, AB and AC respectively.
In △BIL and △CIL,
⇒ BL = LC (Since, AL is the perpendicular bisector of BC)
⇒ ∠BLI = ∠CLI (Both equal to 90°)
⇒ LI = LI (Common side)
∴ △BIL ≅ △CIL (By S.A.S axiom)
⇒ IB = IC …..(1) (Corresponding parts of congruent triangles are equal)
In △CIM and △AIM,
⇒ CM = AM (Since, BM is the perpendicular bisector of AC)
⇒ ∠CMI = ∠AMI (Both equal to 90°)
⇒ MI = MI (Common side)
∴ △CIM ≅ △AIM (By S.A.S axiom)
⇒ IC = IA …..(2) (Corresponding parts of congruent triangles are equal)
From eq.(1) and (2), we get:
⇒ IA = IB = IC.
Hence, proved that IA = IB = IC.
Related Questions
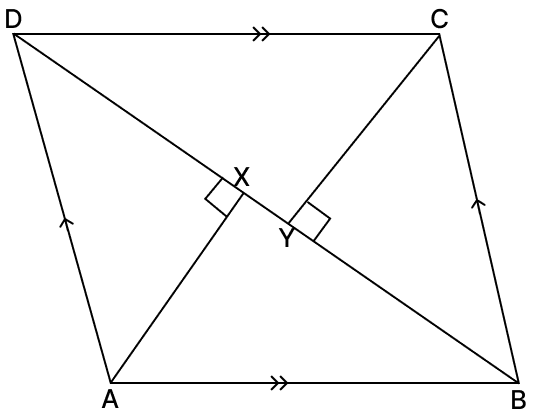
ABCD is a parallelogram in which ∠A and ∠C are obtuse. Points X and Y are taken on diagonal BD such that ∠AXD = ∠CYB = 90°. Prove that : XA = YC.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively such that AB = BE and AD = DF. Prove that △BEC ≅ △DCF.
In a △ABC, AB = AC and ∠A = 50°, find ∠B and ∠C.
In a △ABC, BC = AC and ∠B = 64°, find ∠C.