Mathematics
Use ruler and compass for the following constructions:
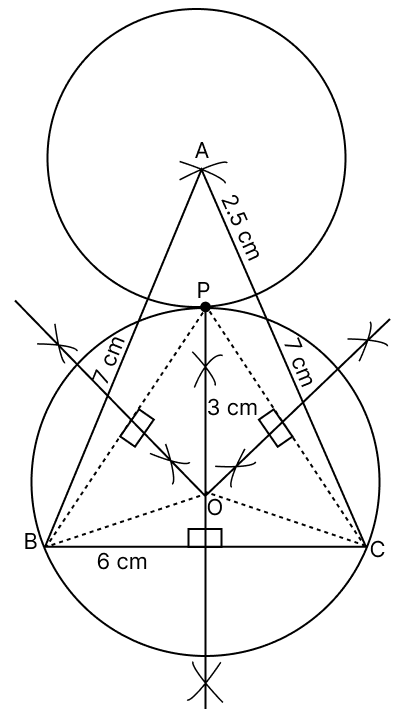
Construct:
(a) an isosceles ΔABC in which AB = AC = 7 cm and BC = 6 cm.
(b) the locus of points which moves such that it is 2.5 cm from the point A.
(c) the locus of points equidistant from B and C. Mark point P which satisfies both the conditions mentioned in (b) and (c).
(d) a circle passing through P, B and C.
Answer
We know that,
The locus of points at a fixed distance from a point, is the circle with fixed point as center and distance as radius.
The locus of points equidistant from two points is the perpendicular bisector of the line joining the two points.
Steps of Construction:
Draw a line segment BC of length 6 cm.
Take point B as the center, use a compass to draw an arc with a radius of 7 cm. With C as the center and radius 7 cm draw another arc that intersects the first arc. Label the point of intersection as A. Join A to B and A to C to form the isosceles triangle ABC.
With A as center and radius 2.5 cm draw a circle.
Construct the perpendicular bisector of the line BC. Mark one of the points where the circle and the perpendicular bisector intersect as P.Join PB and PC.
Draw the perpendicular bisector of PB and PC.
Mark the point as O, where the perpendicular bisectors of PB, BC and PC meet.
With O as center and radius equal to OB draw a circle passing through the points P, B and C.
Related Questions
Use a graph paper for this question:
The Marks out of 80 obtained by 160 students in a Mathematics test were recorded as given in the table:
Marks No. of students 0 - 10 12 10 - 20 20 20 - 30 28 30 - 40 35 40 - 50 29 50 - 60 16 60 - 70 12 70 - 80 8 (Take 2 cm = 10 Marks on one axis and 2 cm = 20 students on the other axis).
Draw an Ogive and use it to find the following:
(a) median marks
(b) upper quartile marks
(c) number of students who scored above 65 marks
(d) the lowest marks scored by the top 30% students.
The angle of elevation of the top of a hill from the foot of a tower at B is 50°. The angle of elevation of the top of the tower 100 m high from the foot of the hill at C is 35°.
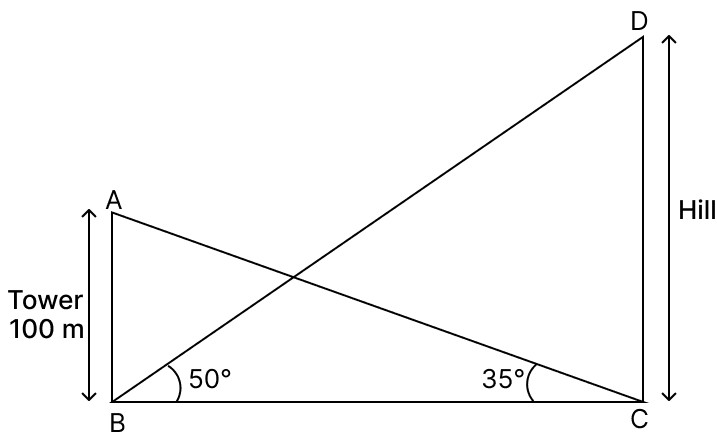
Find the :
(a) horizontal distance BC between the Hill and the Tower.
(b) height CD of the Hill. (Take tan 50° = 1.20)
(c) time taken by a cyclist to cover the distance BC, cycling at 20 m/sec.
Using Remainder and Factor theorem factorise the given polynomial completely.
6x3 + x2 - 4x + 1
Using short-cut method, find mean of the given frequency distribution:
Class Frequency 20 - 30 6 30 - 40 9 40 - 50 14 50 - 60 10 60 - 70 7 70 - 80 4