Mathematics
Using short-cut method, find mean of the given frequency distribution:
| Class | Frequency |
|---|---|
| 20 - 30 | 6 |
| 30 - 40 | 9 |
| 40 - 50 | 14 |
| 50 - 60 | 10 |
| 60 - 70 | 7 |
| 70 - 80 | 4 |
Related Questions
Use a graph paper for this question:
The Marks out of 80 obtained by 160 students in a Mathematics test were recorded as given in the table:
Marks No. of students 0 - 10 12 10 - 20 20 20 - 30 28 30 - 40 35 40 - 50 29 50 - 60 16 60 - 70 12 70 - 80 8 (Take 2 cm = 10 Marks on one axis and 2 cm = 20 students on the other axis).
Draw an Ogive and use it to find the following:
(a) median marks
(b) upper quartile marks
(c) number of students who scored above 65 marks
(d) the lowest marks scored by the top 30% students.
The angle of elevation of the top of a hill from the foot of a tower at B is 50°. The angle of elevation of the top of the tower 100 m high from the foot of the hill at C is 35°.
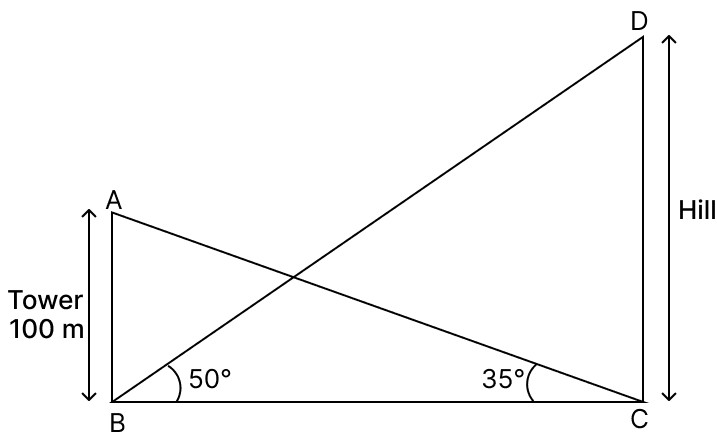
Find the :
(a) horizontal distance BC between the Hill and the Tower.
(b) height CD of the Hill. (Take tan 50° = 1.20)
(c) time taken by a cyclist to cover the distance BC, cycling at 20 m/sec.
Using Remainder and Factor theorem factorise the given polynomial completely.
6x3 + x2 - 4x + 1
Use ruler and compass for the following constructions:
Construct:
(a) an isosceles ΔABC in which AB = AC = 7 cm and BC = 6 cm.
(b) the locus of points which moves such that it is 2.5 cm from the point A.
(c) the locus of points equidistant from B and C. Mark point P which satisfies both the conditions mentioned in (b) and (c).
(d) a circle passing through P, B and C.