Mathematics
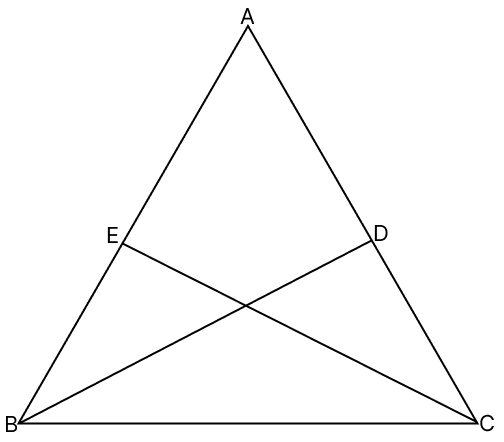
In a △ABC, AB = AC. If the bisectors of ∠B and ∠C meet AC and AB at points D and E respectively, show that :
(i) △DBC ≅ △ECB
(ii) BD = CE
Answer
In △ABC,
AB = AC
⇒ ∠ABC = ∠ACB (Angles opposite to equal sides in a triangle are equal)
Given,
∠ABD = ∠DBC (DB is bisector of ∠B) ….(1)
∠ACE = ∠ECB (CE is bisector of ∠C) ….(2)
Since, ∠ABC = ∠ACB, from eq.(1) and (2), we have:
⇒ ∠ABD = ∠DBC = ∠ACE = ∠ECB
(i) In △ECB and △DBC,
⇒ BC = BC (Common side)
⇒ ∠ECB = ∠DBC (Proved above)
⇒ ∠EBC = ∠DCB (As, ∠ABC = ∠ACB)
∴ △ECB ≅ △DBC (By A.S.A. axiom)
Hence, proved that △ECB ≅ △DBC.
(ii) Since, △ECB ≅ △DBC
BD = CE (Corresponding parts of congruent triangles are equal)
Hence, proved that BD = CE.
Related Questions
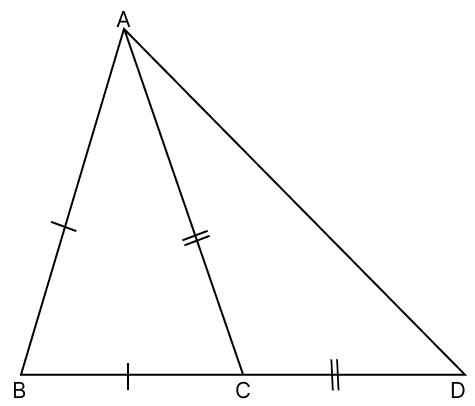
In the given figure, AB = BC and AC = CD. Show that: ∠BAD : ∠ADB = 3 : 1
Show that the perpendiculars drawn from the extremities of the base of an isosceles triangle to the opposite sides are equal.
In an isosceles triangle, prove that the altitude from the vertex bisects the base.
If the altitude from one vertex of a triangle bisects the opposite side, prove that the triangle is isosceles.