Mathematics
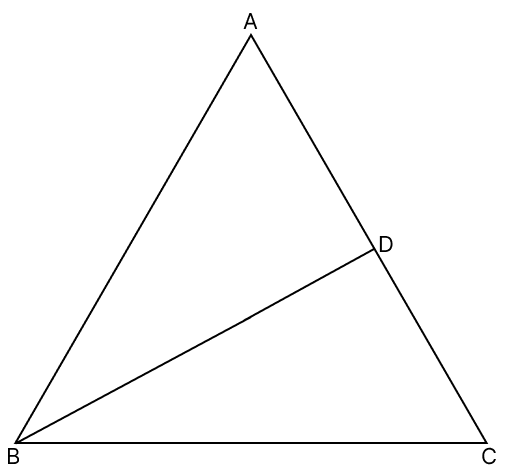
In the adjoining figure, △ABC is equilateral and D is any point on AC. Prove that:
(i) BD > AD
(ii) BD > DC
Answer
(i) Since, ABC is an equilateral triangle.
∴ ∠A = ∠B = ∠C = 60°
In △ ABD,
∠ABD = ∠B - ∠DBC
∴ ∠ABD < ∠B
∴ ∠ABD < ∠A (Since, ∠B = ∠A)
∴ AD < BD or BD > AD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it]
Hence, proved that BD > AD.
(ii) In △ BDC,
∠DBC = ∠B - ∠ABD
∴ ∠DBC < ∠B
∴ ∠DBC < ∠C (∵ ∠B = ∠C)
∴ DC < BD or BD > DC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it]
Hence, proved that BD > DC.
Related Questions
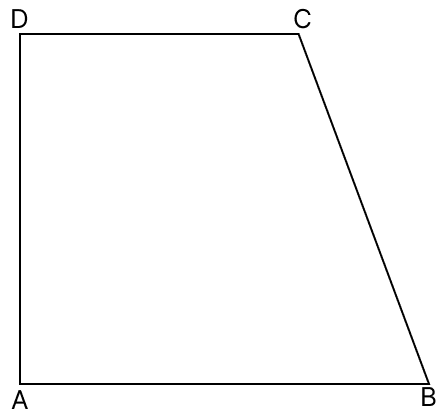
In the adjoining quadrilateral ABCD, AB is the longest side and DC is the shortest side. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B
Can you construct a △ABC in which AB = 5 cm, BC = 4 cm and AC = 9 cm? Give reason.
If O is any point inside △ABC, prove that ∠BOC > ∠A.
In the given figure, AD = AB and AE bisects ∠A. Prove that:
(i) BE = ED
(ii) ∠ABD > ∠BCA