Mathematics
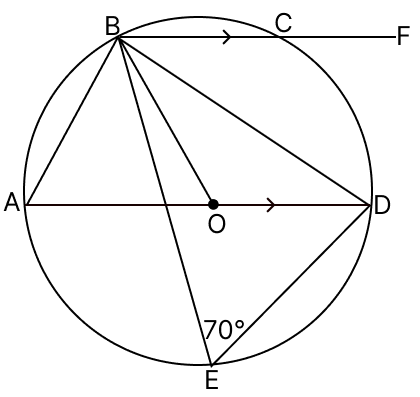
In the adjoining figure of a circle with centre O and diameter AD, ∠BED = 70° and BC is parallel to AD. Find:
(a) ∠BAD
(b) ∠BOD
(c) ∠DBC
(d) ∠DCF
Answer
(a) Given,
∠BED = 70°
We know that,
Angles in the same segment of a circle are equal.
∠BAD = ∠BED = 70°.
Hence, ∠BAD = 70°.
(b) We know that,
The angle which an arc of a circle subtends at the center is double which it subtends at any point on the remaining part of the circumference.
Therefore,
∠BOD = 2∠BAD = 2 × 70° = 140°.
Hence, ∠BOD = 140°.
(c) We know that,
Angle in a semi-circle is a right angle triangle.
∠ABD = 90°
In △ABD,
⇒ ∠BAD + ∠BDA + ∠ABD = 180°
⇒ 70° + ∠BDA + 90° = 180°
⇒ 160° + ∠BDA = 180°
⇒ ∠BDA = 180° - 160°
⇒ ∠BDA = 20°
From figure,
BC || AD
∴ ∠DBC = ∠BDA = 20° (Alternate angles are equal).
Hence, ∠DBC = 20°.
(d) The figure ABCD is a cyclic quadrilateral
We know that,
The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
∠DCF = ∠BAD = 70°.
Hence, ∠DCF = 70°.
Related Questions
164, 160, 156, 152, ….. are in Arithmetic Progression (A.P.). Find :
(a) which term is equal to 0.
(b) the sum of its first 20 terms.
Solve the following quadratic equation:
3x2 + 6x - 4 = 0
Give your answer correct to two places of decimals.
If the 6th term of a series in Geometric Progression (G.P.) is 32 and the 9th term is 256, find the:
(a) first term and the common ratio.
(b) sum of its first 10 terms.