Mathematics
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Answer
Let ABC be an isosceles triangle with AB = AC.
Base BC is produced at points E, D respectively.
AB = AC
⇒ ∠ABC = ∠ACB = x (let) (Angles opposite to equal sides in a triangle are equal)
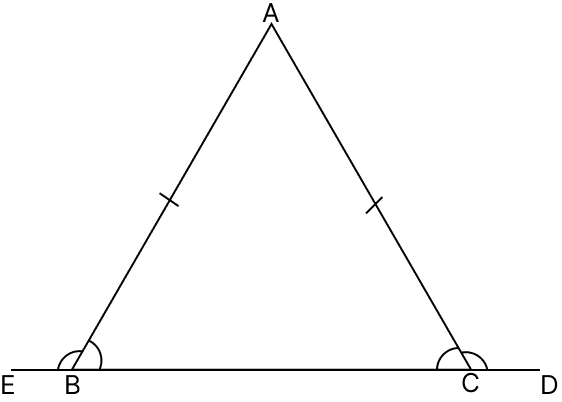
From figure,
⇒ ∠ACD + ∠ACB = 180° (Linear pair)
⇒ ∠ACD + x = 180°
⇒ ∠ACD = 180° - x ….(1)
From figure,
⇒ ∠ABE + ∠ABC = 180° (Linear pair)
⇒ ∠ABE + x = 180°
⇒ ∠ABE = 180° - x ….(2)
From eq.(1) and (2), we have:
⇒ ∠ABE = ∠ACD
Hence, proved that the exterior angles so formed are equal to each other.
Related Questions
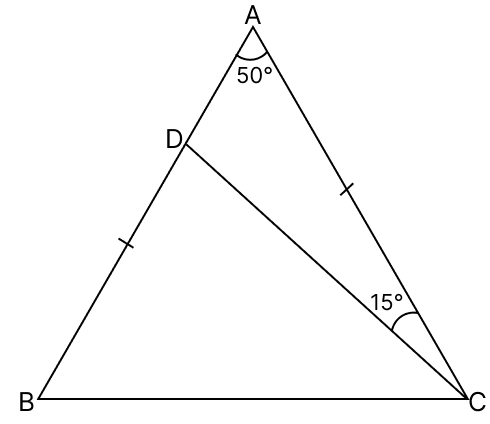
In the given figure, AB = AC; ∠A = 50° and ∠ACD = 15°. Show that BC = CD.
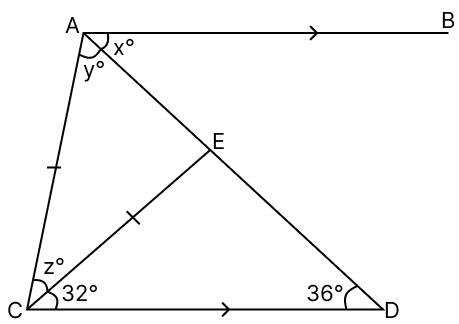
In the given figure, AB || CD and CA = CE. Find the values of x, y and z.
In the given figure, side CA of △ABC has been produced to E. If AC = AD = BD; ∠ACD = 46° and ∠BAE = x°; find the value of x.
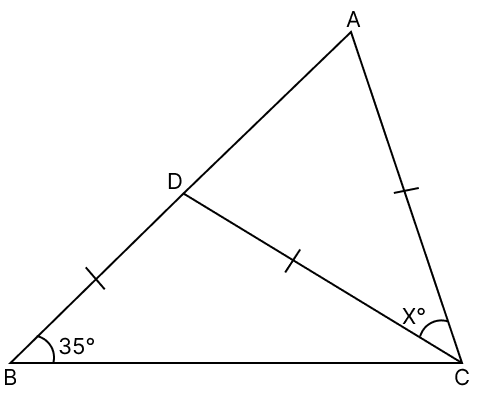
In the given figure, CA = CD = BD; ∠DBC = 35° and ∠DCA = x°. Find the value of x.