Mathematics
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Triangles
1 Like
Answer
Let ABC be an isosceles triangle with AB = AC.
Base BC is produced at points E, D respectively.
AB = AC
⇒ ∠ABC = ∠ACB = x (let) (Angles opposite to equal sides in a triangle are equal)
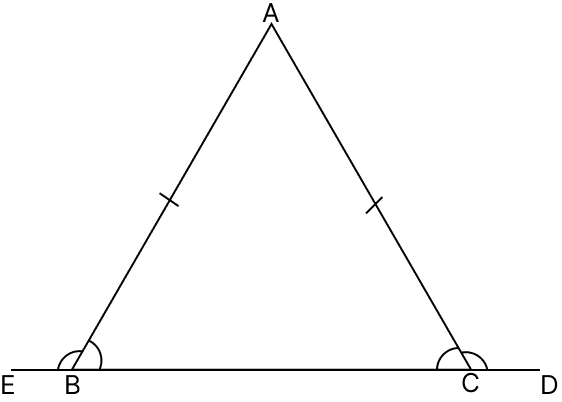
From figure,
⇒ ∠ACD + ∠ACB = 180° (Linear pair)
⇒ ∠ACD + x = 180°
⇒ ∠ACD = 180° - x ….(1)
From figure,
⇒ ∠ABE + ∠ABC = 180° (Linear pair)
⇒ ∠ABE + x = 180°
⇒ ∠ABE = 180° - x ….(2)
From eq.(1) and (2), we have:
⇒ ∠ABE = ∠ACD
Hence, proved that the exterior angles so formed are equal to each other.
Answered By
2 Likes
Related Questions
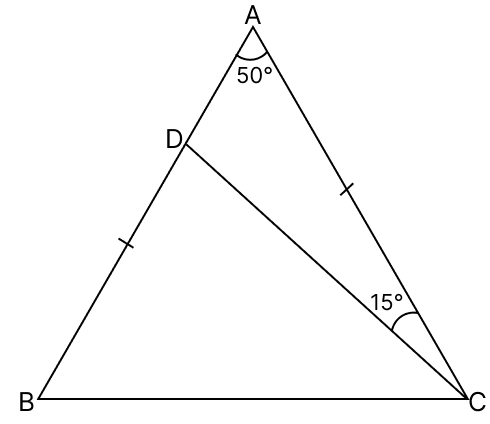
In the given figure, AB = AC; ∠A = 50° and ∠ACD = 15°. Show that BC = CD.
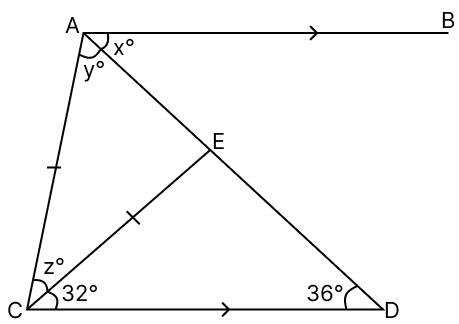
In the given figure, AB || CD and CA = CE. Find the values of x, y and z.
In the given figure, side CA of △ABC has been produced to E. If AC = AD = BD; ∠ACD = 46° and ∠BAE = x°; find the value of x.
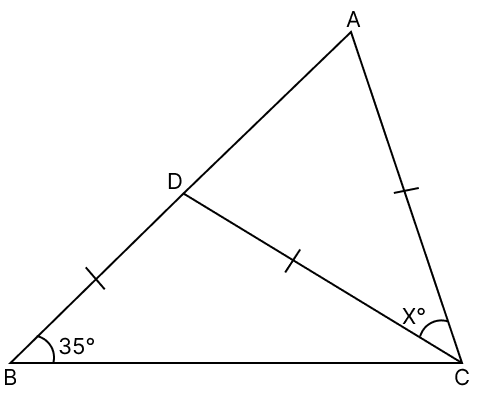
In the given figure, CA = CD = BD; ∠DBC = 35° and ∠DCA = x°. Find the value of x.