Case Study

Ms Anu Gupta teaches mathematics to class 9 in a school. One day she drew a figure on the board in the class. She provided the following clues to the students.

AB || CD

O is the mid-points of AD

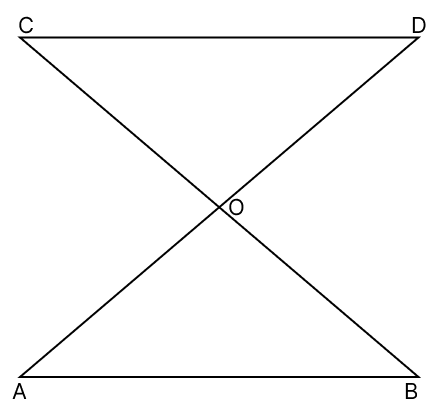
Based on this information, answer the following questions:

1. △OAB ≅ △ODC by which of the following congruent condition?
   (a) SAS
   (b) ASA
   (c) SSS
   (d) RHS

2. ∠AOB = ∠DOC holds because:
   (a) Alternate angles are equal
   (b) Corresponding angles are equal
   (c) Vertically opposite angles are equal
   (d) None of these

3. Which of the following is correct?
   (a) ∠A = ∠C
   (b) ∠B = ∠D
   (c) ∠B = ∠C
   (d) ∠AOB = ∠OCB

4. Which of the following is correct?
   (a) AO = OB
   (b) AB = OB
   (c) OD = CD
   (d) OC = OB

5. Which of the following is not a congruent condition?
   (a) ASA
   (b) SSS
   (c) AAA
   (d) AAS

1. Given,

AB || CD

In △OAB and △ODC,

⇒ AO = DO (∵ O is the mid-point of AD)

⇒ ∠BAO = ∠CDO (Alternate angles are equal)

⇒ ∠AOB = ∠DOC (Vertically opposite angles are equal)

∴ △OAB ≅ △ODC (By A.S.A axiom)

Hence, option (b) is the correct option.

2. ∠AOB and ∠DOC are vertically opposite angles, which are always equal.

Hence, option (c) is the correct option.

3. Since, △OAB ≅ △ODC

⇒ ∠B = ∠C (Corresponding parts of congruent triangle are equal.)

Hence, option (c) is the correct option.

4. Since, △OAB ≅ △ODC

⇒ OC = OB (Corresponding parts of congruent triangles are equal)

Hence, option (d) is the correct option.

5. Angle-Angle-Angle(AAA) ensures corresponding angles are equal but corresponding sides of a triangle may vary.

Thus, AAA is not a congruent condition.

Hence, option (c) is the correct option.