Mathematics
Assertion (A): If three angles of a triangle are equal to the corresponding three angles of another triangle, then the triangles are congruent.
Reason (R): Two triangles are said to be congruent, if and only if, one of them can be made to superimpose on the other so as to cover exactly.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
Triangles
1 Like
Answer
If three angles of a triangle are equal to the corresponding three angles of another triangle, then the triangles are similar not necessarily congruent.
∴ Assertion (A) is false.
Two triangles are said to be congruent, if both corresponding sides and angles to be equal i.e. once of triangle can be made to superimpose on other.
∴ Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Case Study
Ms Anu Gupta teaches mathematics to class 9 in a school. One day she drew a figure on the board in the class. She provided the following clues to the students.
AB || CD
O is the mid-points of AD
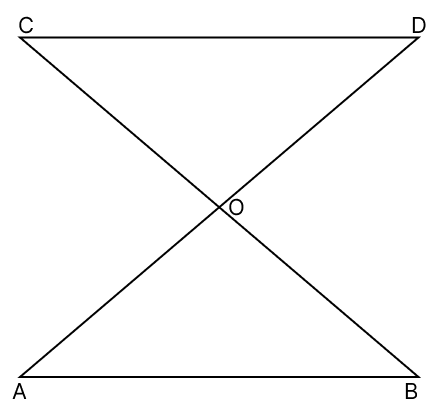
Based on this information, answer the following questions:
△OAB ≅ △ODC by which of the following congruent condition?
(a) SAS
(b) ASA
(c) SSS
(d) RHS∠AOB = ∠DOC holds because:
(a) Alternate angles are equal
(b) Corresponding angles are equal
(c) Vertically opposite angles are equal
(d) None of theseWhich of the following is correct?
(a) ∠A = ∠C
(b) ∠B = ∠D
(c) ∠B = ∠C
(d) ∠AOB = ∠OCBWhich of the following is correct?
(a) AO = OB
(b) AB = OB
(c) OD = CD
(d) OC = OBWhich of the following is not a congruent condition?
(a) ASA
(b) SSS
(c) AAA
(d) AAS
Assertion (A): The orthocentre of a triangle may lie in the exterior of the triangle.
Reason (R): The point of intersection of the medians of a triangle is called its orthocentre.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
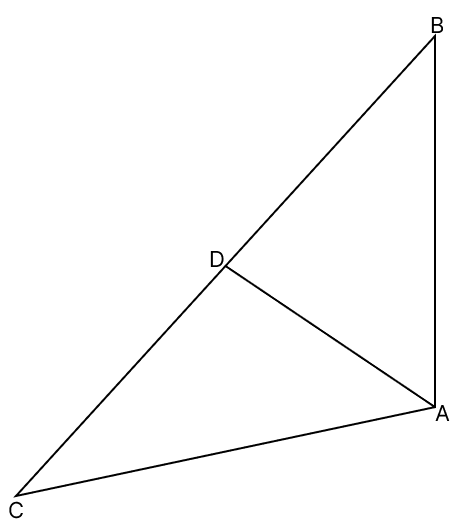
Assertion (A): In △ABC, D is a point on side BC. AB + BC + AC > 2AD
Reason (R): Sum of two sides of a triangle is greater than the third side.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
In the given figure, the bisectors of ∠B and ∠C intersect each other at O and ∠BAC = 50°. The measure of ∠BOC is :
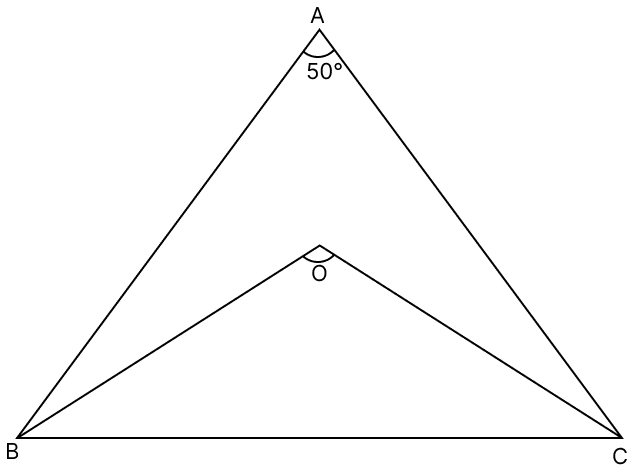
100°
115°
130°
140°