Mathematics
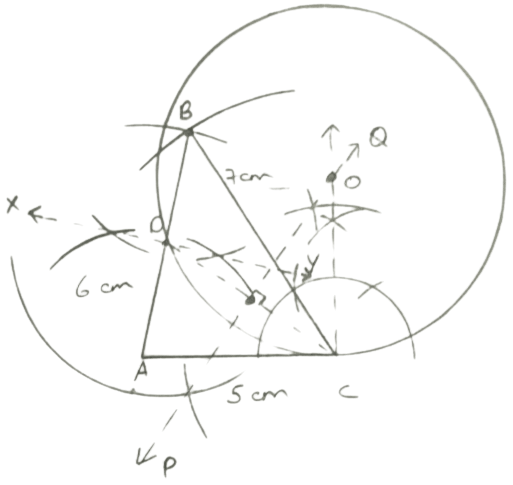
Construct a triangle ABC in which AC = 5 cm, BC = 7 cm and AB = 6 cm.
(i) Mark D, the mid-point of AB.
(ii) Construct a circle which touches BC at C and passes through D.
Answer
Steps of construction :
Draw a line segment AC = 5 cm.
From A draw an arc of radius 6 cm and from C draw an arc of radius 7 cm, intersecting each other at point B.
Draw XY, the perpendicular bisector of AB, and mark D as the mid point.
Draw perpendicular bisector of CD.
From C, draw a line segment perpendicular to AC, which intersect the PQ, perpendicular bisector of CD at O.
Take O as centre and OD as radius draw a circle.
Related Questions
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
Prove that the line NM produced bisects AB at P.

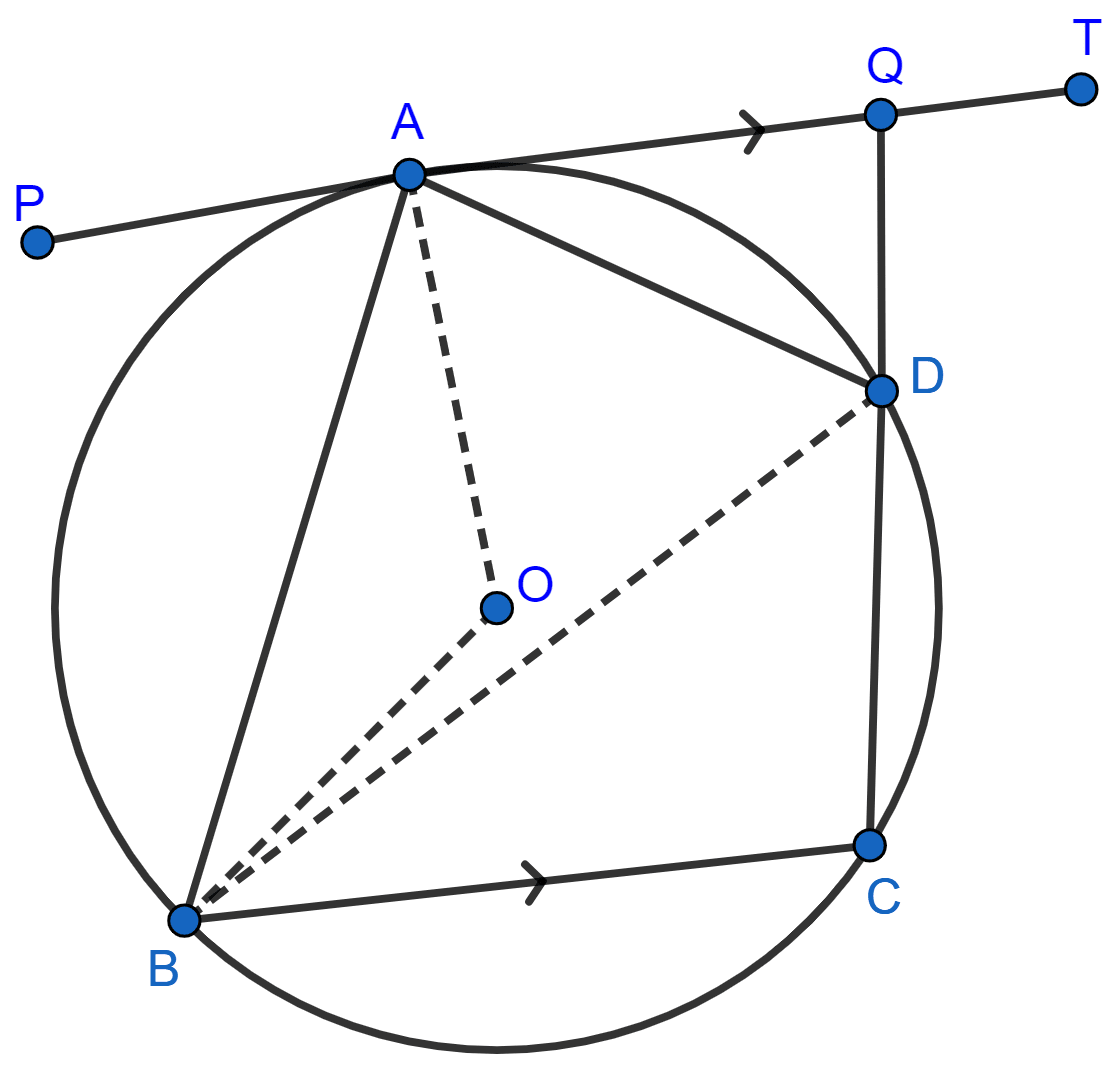
In the given figure, PAT is tangent to the circle with center O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that :
(i) ∠BAP = ∠ADQ
(ii) ∠AOB = 2∠ADQ
(iii) ∠ADQ = ∠ADB.
Using ruler and compasses only; draw a circle of radius 4 cm. Produce AB, a diameter of this circle, upto point X so that BX = 4 cm. Construct a circle to touch AB at X and to touch the circle, drawn earlier, externally.