Mathematics
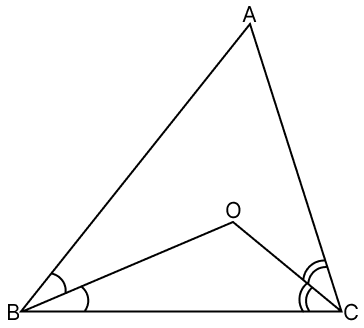
In the given figure, AB > AC. If BO and CO are the bisectors of ∠B and ∠C respectively, prove that BO > CO.
Answer
Given,
BO and CO are the bisectors of ∠B and ∠C respectively.
⇒ ∠ABO = ∠OBC and ∠ACO = ∠OCB
Given,
AB > AC
We know that angle opposite to the greater side is greater.
∴ ∠ACB > ∠ABC
⇒ ∠ACO + ∠OCB > ∠ABO + ∠OBC
⇒ ∠OCB + ∠OCB > ∠OBC + ∠OBC (∵ ∠ABO = ∠OBC and ∠ACO = ∠OCB)
⇒ 2∠OCB > 2∠OBC
⇒ ∠OCB > ∠OBC
In △BOC,
We know that side opposite to the greater angle is greater.
⇒ BO > CO.
Hence, proved that BO > CO.
Related Questions
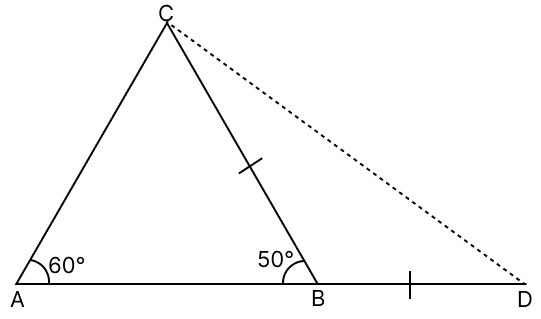
In the given figure, side AB of △ABC is produced to D such that BD = BC. If ∠A = 60° and ∠B = 50°, prove that :
(i) AD > CD
(ii) AD > AC
In a right angled triangle, prove that the hypotenuse is the longest side.
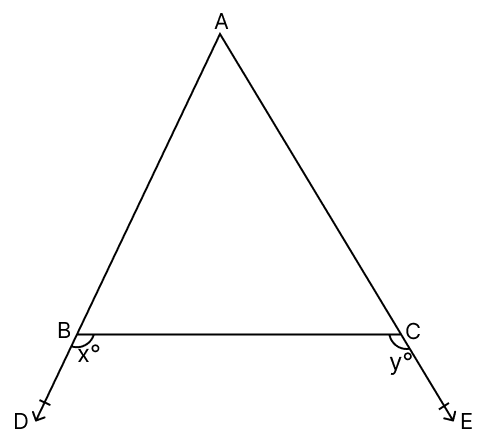
In the given figure, sides AB and AC of △ABC have been produced to D and E respectively. If ∠CBD = x° and ∠BCE = y° such that x > y, show that AB > AC.
In the given figure, sides AB = AC. Show that AD > AB.