Mathematics
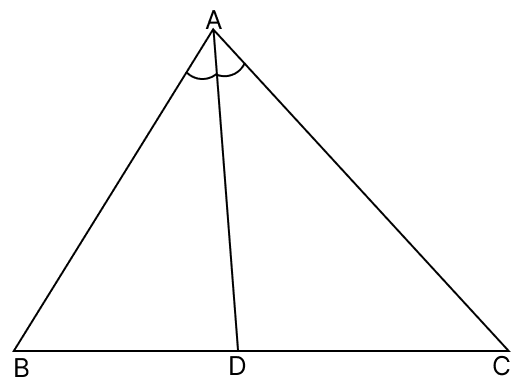
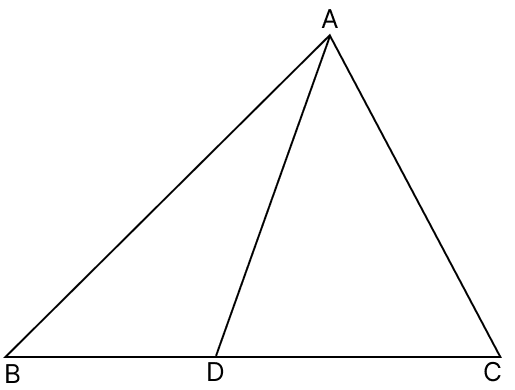
In the given figure, sides AB = AC. Show that AD > AB.
Triangles
1 Like
Answer
In △ABC,
⇒ ∠ABC = ∠ACB [As, AC = AB and angle opposite to equal sides are equal]
We know that,
In an isosceles triangle, the base angles are acute as only one obtuse angle can exist in a triangle.
∴ ∠ABC and ∠ACB are acute angles.
From figure,
DBC is a straight line.
⇒ ∠ABD + ∠ABC = 180° [Linear pair]
⇒ ∠ABD = 180° - ∠ABC
Since, ∠ABC is an acute angle thus, ∠ABD is an obtuse angle.
∴ In △ABD, ∠ABD is the largest angle.
∴ ∠ABD > ∠ADB
∴ AD > AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)
Hence, proved that AD > AB.
Answered By
2 Likes
Related Questions
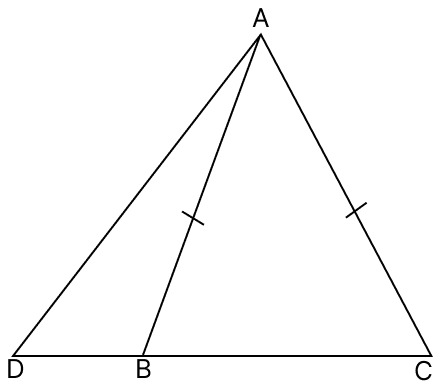
In the given figure, AB > AC. If BO and CO are the bisectors of ∠B and ∠C respectively, prove that BO > CO.
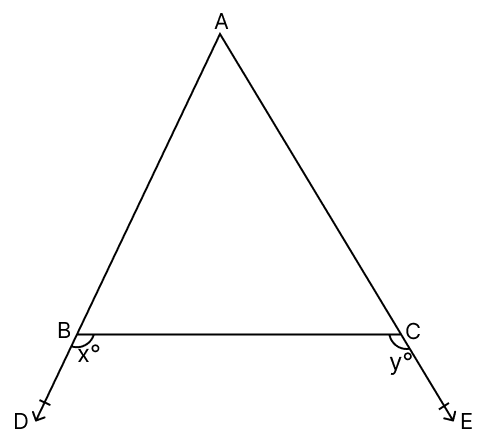
In the given figure, sides AB and AC of △ABC have been produced to D and E respectively. If ∠CBD = x° and ∠BCE = y° such that x > y, show that AB > AC.
In the adjoining figure, AB > AC and D is any point on BC. Show that AB > AD
In the adjoining figure, AC > AB and AD is the bisector of ∠A. Show that : ∠ADC > ∠ADB