Mathematics
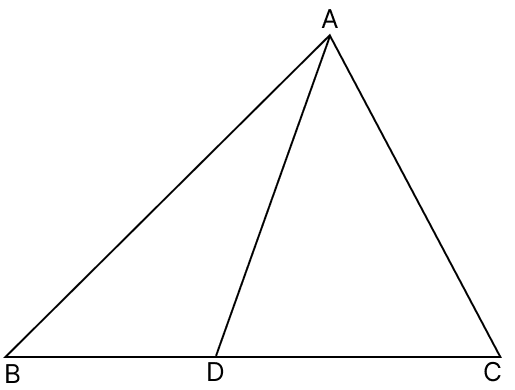
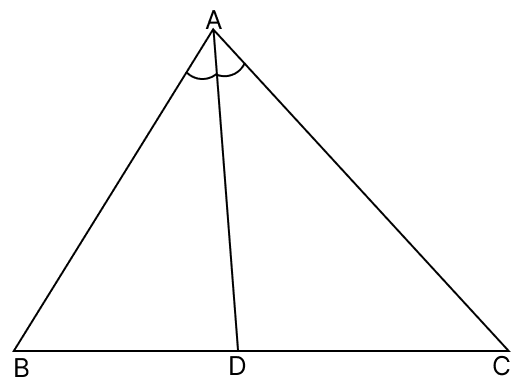
In the adjoining figure, AB > AC and D is any point on BC. Show that AB > AD
Triangles
1 Like
Answer
Given,
AB > AC
∴ ∠ACB > ∠ABC (As angle opposite to greater side is greater)
From figure,
∠ADB = ∠ACD + ∠DAC (As exterior angle is equal to sum of two opposite interior angles)
⇒ ∠ADB > ∠ACD
⇒ ∠ADB > ∠ACB
⇒ ∠ADB > ∠ABC [∵ ∠ACB > ∠ABC]
⇒ ∠ADB > ∠ABD
∴ AB > AD (As side opposite to greater angle is greater)
Hence, proved that AB > AD.
Answered By
3 Likes
Related Questions
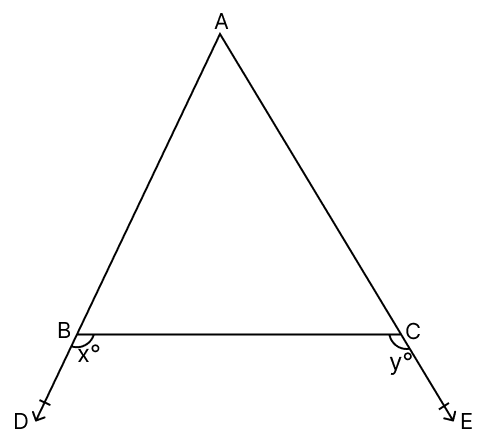
In the given figure, sides AB and AC of △ABC have been produced to D and E respectively. If ∠CBD = x° and ∠BCE = y° such that x > y, show that AB > AC.
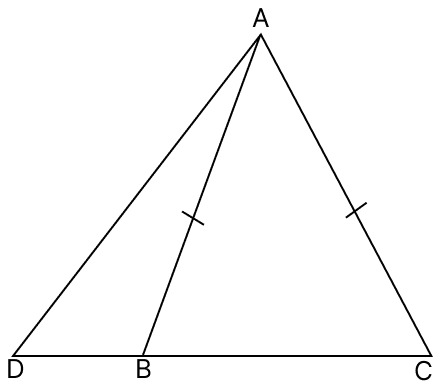
In the given figure, sides AB = AC. Show that AD > AB.
In the adjoining figure, AC > AB and AD is the bisector of ∠A. Show that : ∠ADC > ∠ADB
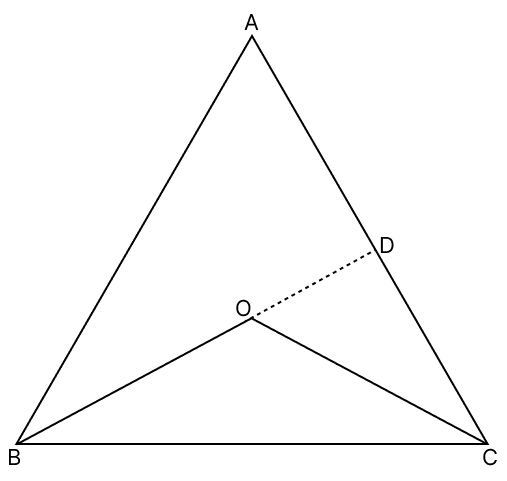
In the adjoining figure, in △ABC, O is any point in its interior. Show that: OB + OC < AB + AC