Mathematics
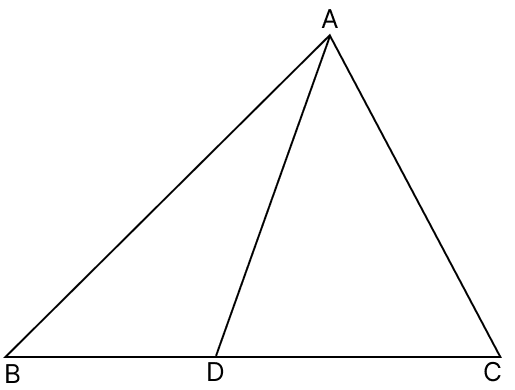
In the adjoining figure, AC > AB and AD is the bisector of ∠A. Show that : ∠ADC > ∠ADB
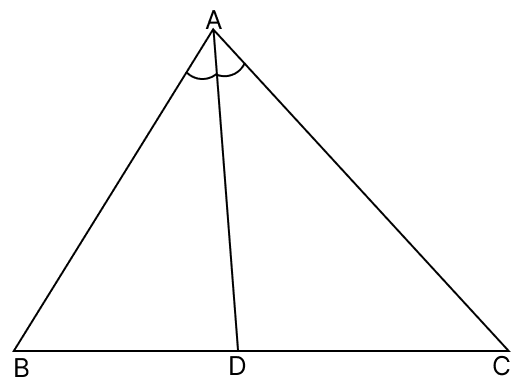
Triangles
1 Like
Answer
We know that,
In a triangle an exterior angle is equal to the sum of two opposite interior angles.
In △ADC,
⇒ ∠ADB = ∠CAD + ∠C …..(1)
In △ADB,
⇒ ∠ADC = ∠BAD + ∠B …..(2)
In △ABC,
⇒ AC > AB (Given)
⇒ ∠B > ∠C [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]
Since, AD is the bisector of angle A.
∴ ∠BAD + ∠B > ∠CAD + ∠C ……(3)
From eq.(1), (2) and (3), we get:
⇒ ∠ADC > ∠ADB
Hence, proved that ∠ADC > ∠ADB.
Answered By
2 Likes