Mathematics
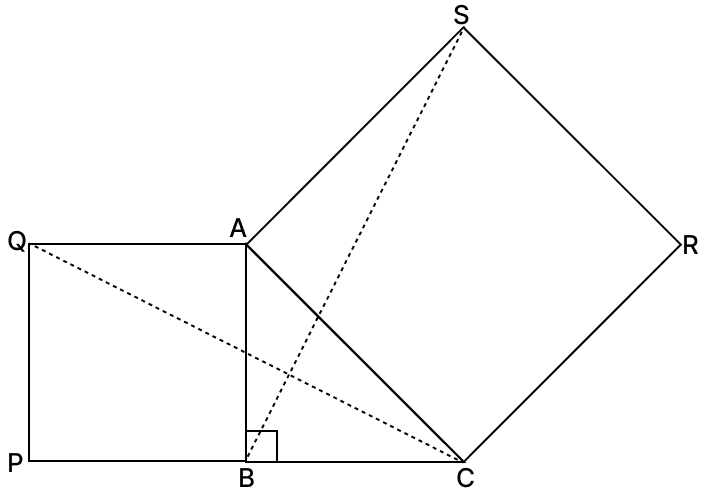
In the given figure, in △ABC, ∠B = 90°. If ABPQ and ACRS are squares, prove that:
(i) △ACQ ≅ △ABS
(ii) CQ = BS.
Answer
(i) From figure,
In △ACQ,
⇒ ∠BAC = ∠QAC - ∠QAB
⇒ ∠QAC = ∠BAC + ∠QAB
⇒ ∠QAC = ∠BAC + 90° ….(1)
In △ABS,
⇒ ∠BAC = ∠BAS - ∠CAS
⇒ ∠BAS = ∠BAC + ∠CAS
⇒ ∠BAS = ∠BAC + 90° ….(2)
From eq.(1) and (2), we have:
⇒ ∠QAC = ∠BAS
In △ACQ and △ABS,
⇒ ∠QAC = ∠BAS [Proved above]
⇒ AQ = AB [Sides of square ABPQ]
⇒ AC = AS [Sides of square ACRS]
∴ △ACQ ≅ △ABS (By S.A.S axiom)
Hence, proved that △ACQ ≅ △ABS.
(ii) As,
△ACQ ≅ △ABS
∴ CQ = BS [Corresponding parts of congruent triangles are equal]
Hence, proved that CQ = BS.
Related Questions
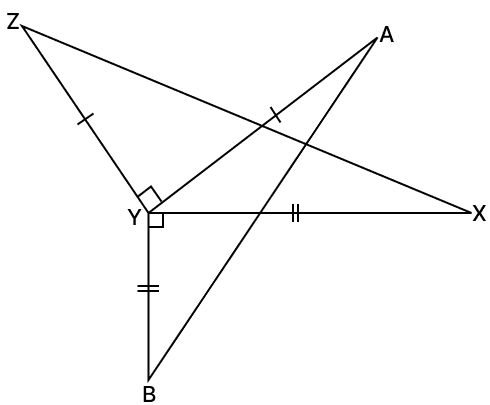
In the given figure, AY ⊥ ZY nd BY ⊥ XY such that AY = ZY and BY = XY. Prove that AB = ZX.
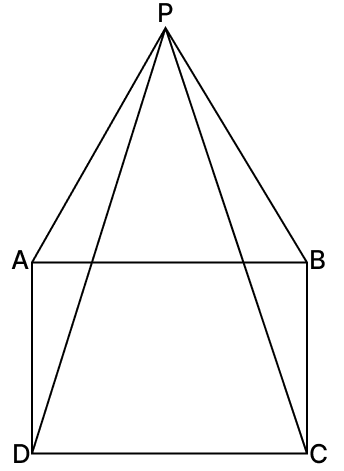
In the given figure, ABCD is a square and △PAB is an equilateral triangle.
(i) Prove that △APD ≅ △BPC.
(ii) Show that ∠DPC = 15°.
Squares ABPQ and ADRS are drawn on the sides AB and AD of a parallelogram ABCD. Prove that:
(i) ∠SAQ = ∠ABC
(ii) SQ = AC.
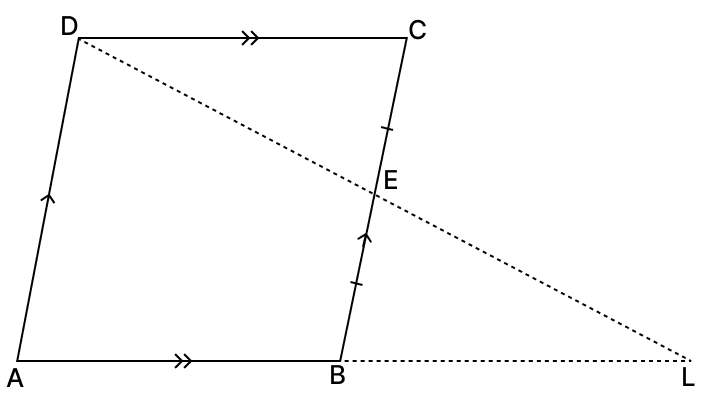
In the given figure, ABCD is a parallelogram, E is the mid-point of BC. DE produced meets AB produced at L. Prove that:
(i) AB = BL
(ii) AL = 2DC