Mathematics
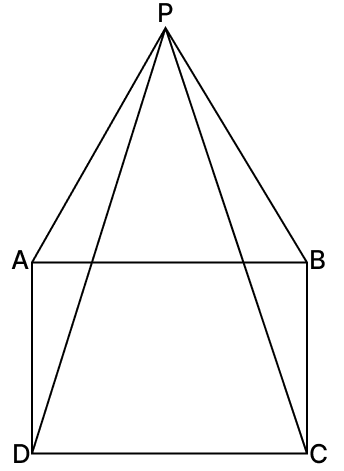
In the given figure, ABCD is a square and △PAB is an equilateral triangle.
(i) Prove that △APD ≅ △BPC.
(ii) Show that ∠DPC = 15°.
Triangles
3 Likes
Answer
(i) We know that,
Each interior angle in a square is 90° and each interior angle in an equilateral triangle is 60°.
From figure,
⇒ ∠DAP = ∠DAB + ∠BAP
⇒ ∠DAP = 90° + 60° = 150°
⇒ ∠CBP = ∠CBA + ∠ABP
⇒ ∠CBP = 90° + 60° = 150°
In △APD and △BPC,
⇒ ∠DAP = ∠CBP [Each equal to 150°]
⇒ AD = BC [Sides of a square]
⇒ AP = BP [Sides of an equilateral triangle]
∴ △APD ≅ △BPC (By S.A.S axiom)
Hence, △APD ≅ △BPC.
(ii) ABCD is a square.
∴ AB = AD = DC = BC
APB is an equilateral triangle.
∴ AP = PB = AB
So, we get :
AP = AD and PB = BC
∴ △APD and △BPC are isosceles triangle.
We know that,
Angles opposite to equal sides are equal.
∴ ∠APD = ∠ADP = x (let) and ∠BPC = ∠BCP = y (let)
In △APD,
By angle sum property of triangle,
⇒ ∠APD + ∠ADP + ∠DAP = 180°
⇒ x + x + 150° = 180°
⇒ 2x = 180° - 150°
⇒ 2x = 30°
⇒ x =
⇒ x = 15°.
In △BPC,
By angle sum property of triangle,
⇒ ∠BPC + ∠BCP + ∠PBC = 180°
⇒ y + y + 150° = 180°
⇒ 2y = 180° - 150°
⇒ 2y = 30°
⇒ y =
⇒ y = 15°
From figure,
⇒ ∠PDC = ∠ADC - ∠ADP = 90° - 15° = 75°
⇒ ∠PCD = ∠BCD - ∠BCP = 90° - 15° = 75°
In △DPC,
By angle sum property of triangle,
⇒ ∠DPC + ∠PDC + ∠PCD = 180°
⇒ ∠DPC + 75° + 75° = 180°
⇒ ∠DPC + 150° = 180°
⇒ ∠DPC = 180° - 150°
⇒ ∠DPC = 30°.
Hence, proved that ∠DPC = 30°.
Answered By
3 Likes
Related Questions
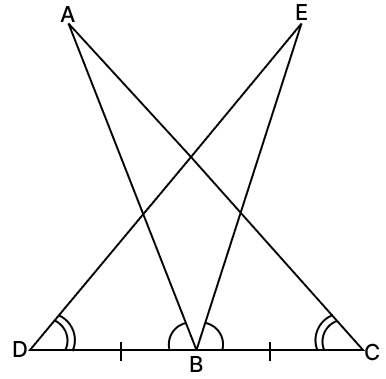
In the given figure, ∠ABD = ∠EBC, BD = BC and ∠ACB = ∠EDB. Prove that AB = BE.
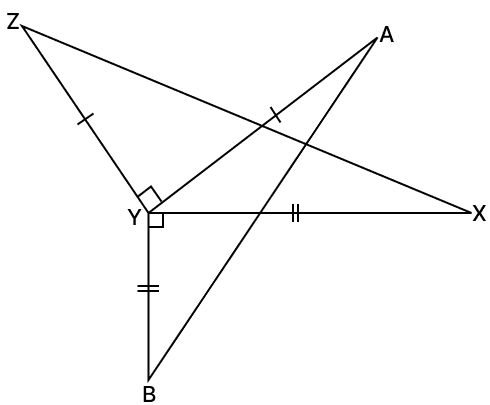
In the given figure, AY ⊥ ZY nd BY ⊥ XY such that AY = ZY and BY = XY. Prove that AB = ZX.
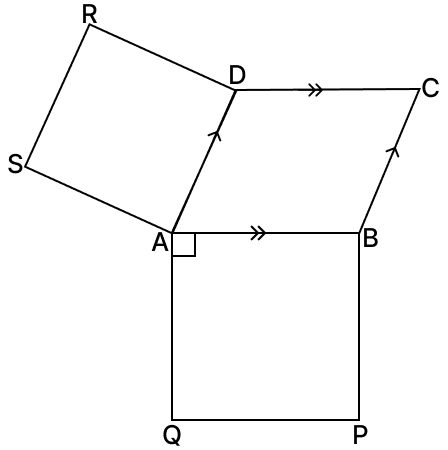
In the given figure, in △ABC, ∠B = 90°. If ABPQ and ACRS are squares, prove that:
(i) △ACQ ≅ △ABS
(ii) CQ = BS.
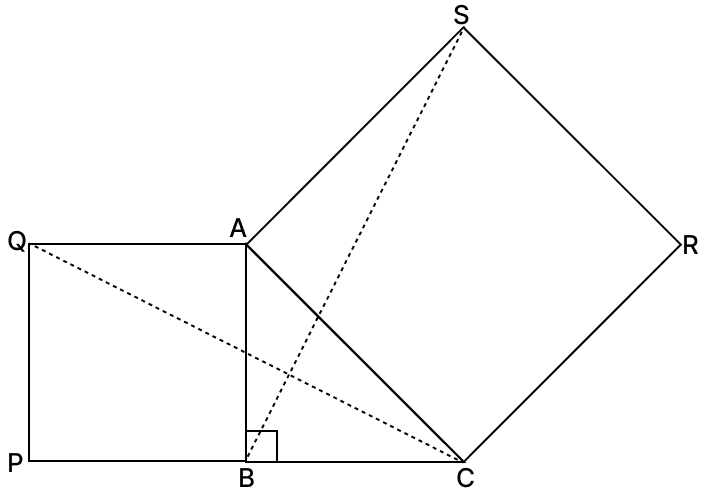
Squares ABPQ and ADRS are drawn on the sides AB and AD of a parallelogram ABCD. Prove that:
(i) ∠SAQ = ∠ABC
(ii) SQ = AC.