Mathematics
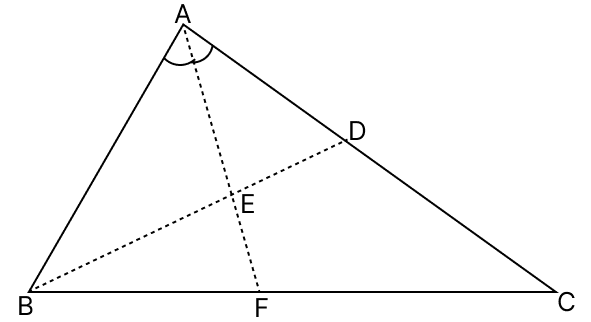
In the given figure, AD = AB and AE bisects ∠A. Prove that:
(i) BE = ED
(ii) ∠ABD > ∠BCA
Answer
In △ABE and △ADE,
⇒ AE = AE (Common side)
⇒ AB = AD (Given)
⇒ ∠BAE = ∠DAE (∵ AE bisects ∠A)
∴ △ABE ≅ △ADE (By S.A.S axiom)
(i) Since, △ABE ≅ △ADE
We know that,
Corresponding parts of congruent triangle are equal.
∴ BE = ED
Hence, proved that BE = ED.
(ii) Since, △ABE ≅ △ADE
We know that,
Corresponding parts of congruent triangle are equal.
∴ ∠ABE = ∠ADE
⇒ ∠ABD = ∠ADB
From figure,
⇒ ∠BDA > ∠BCA (∵ Exterior angle is greater than interior opposite angle)
⇒ ∠ABD > ∠BCA
Hence, proved that ∠ABD > ∠BCA.
Related Questions
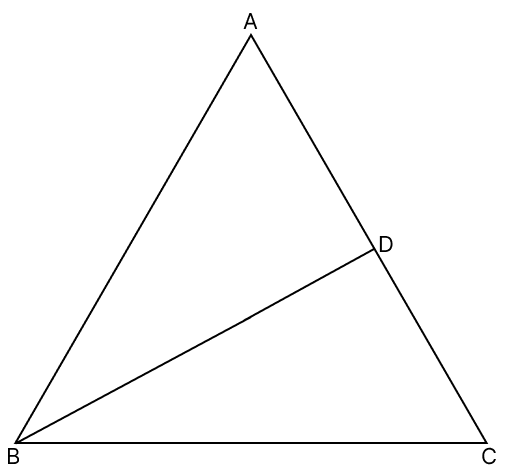
In the adjoining figure, △ABC is equilateral and D is any point on AC. Prove that:
(i) BD > AD
(ii) BD > DC
If O is any point inside △ABC, prove that ∠BOC > ∠A.
The sides AB and AC of △ABC are produced to D and E respectively and the bisectors of ∠CBD and ∠BCE meet at O. If AB > AC, prove that OC > OB.
In △ABC, AB = 7.5 cm, BC = 6.2 cm and AC = 5.4 cm. Name :
(i) the least angle
(ii) the greatest angle of the triangle