Mathematics
Answer
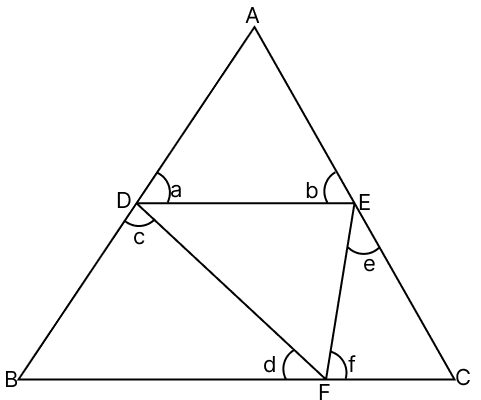
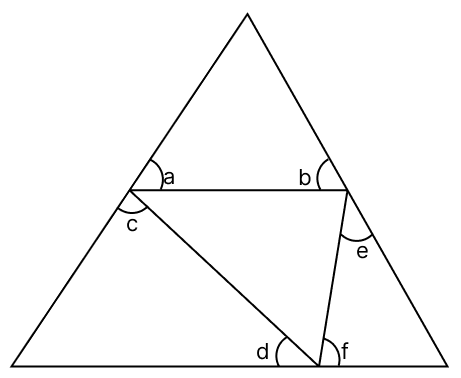
In △AED,
⇒ a + b + ∠A = 180° ….(1)
In △DBF,
⇒ c + d + ∠B = 180° ….(2)
In △EFC,
⇒ e + f + ∠C = 180° ….(3)
In △ABC,
⇒ ∠A + ∠B + ∠C = 180° ….(4)
Adding eq.(1), (2) and (3), we get :
⇒ a + b + c + d + e + f + ∠A + ∠B + ∠C = 180° + 180° + 180°
⇒ a + b + c + d + e + f + 180° = 540°
⇒ a + b + c + d + e + f = 540° - 180°
⇒ a + b + c + d + e + f = 360°.
Hence, the value of a + b + c + d + e + f = 360°.
Related Questions
ABC is a triangle in which AC = BC and ∠BAC = 50°. Side BC is produced to D such that BC = CD. ∠BAD is equal to :
45°
50°
90°
100°
ABD is a triangle such that ∠ADB = 20° and C is a point on BD such that AB = AC and CD = CA. The measure of ∠ABC :
40°
50°
55°
60°
The lengths of the three sides of a triangle are 4 cm, 5 cm, and 7 cm. Which of the following cannot be the length of any one of the medians?
2.5 cm
3.8 cm
5 cm
None of these
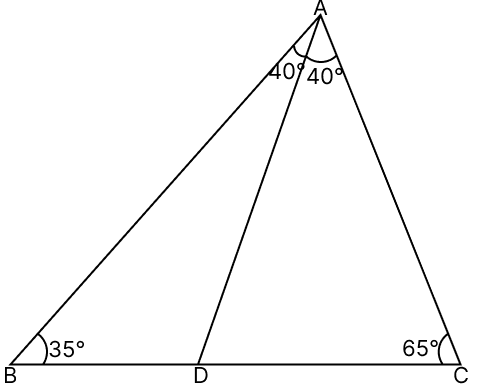
In △ABC, ∠B = 35°, ∠C = 65° and the bisector AD of ∠BAC meets BC at D. Arrange the sides AD, BD and CD in ascending order of their lengths.