Mathematics
The lengths of the three sides of a triangle are 4 cm, 5 cm, and 7 cm. Which of the following cannot be the length of any one of the medians?
2.5 cm
3.8 cm
5 cm
None of these
Triangles
1 Like
Answer
Suppose there is a triangle with sides of length a, b and c, then the median to side a is always less than the sum of other two sides.
Thus, in this case each of the following options can be the length of the median of triangle.
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
ABC is a triangle in which AC = BC and ∠BAC = 50°. Side BC is produced to D such that BC = CD. ∠BAD is equal to :
45°
50°
90°
100°
ABD is a triangle such that ∠ADB = 20° and C is a point on BD such that AB = AC and CD = CA. The measure of ∠ABC :
40°
50°
55°
60°
In △ABC, ∠B = 35°, ∠C = 65° and the bisector AD of ∠BAC meets BC at D. Arrange the sides AD, BD and CD in ascending order of their lengths.
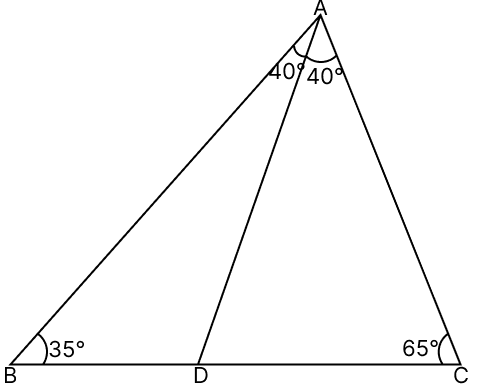
In the given figure, find the value of a + b + c + d + e + f.