Mathematics
Given that PQRS is a cyclic quadrilateral and also its diagonals bisect each other. What can you conclude about the quadrilateral?
Answer
Let PQRS be a cyclic quadrilateral.
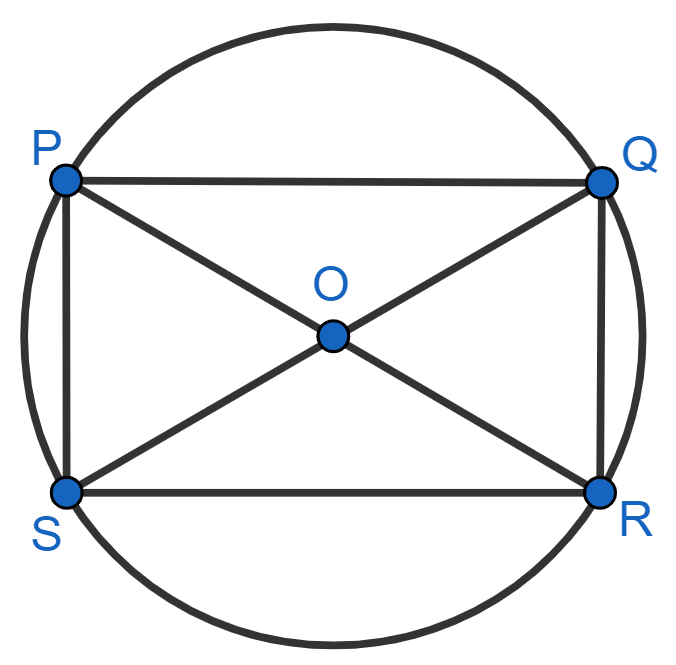
Given,
Diagonals bisect each other.
∴ PO = OR and SO = OQ.
From figure,
⇒ PO + OR = PR
⇒ PO + PO = PR
⇒ 2PO = PR
Since, PR is the diameter of the circle.
So, we can say that PO is the radius of the circle and OR is also the radius.
From figure,
⇒ SO + OQ = SQ
⇒ SO + SO = SQ
⇒ 2SO = SQ
Since, SQ is the diameter of the circle.
So, we can say that SO is the radius of the circle and OQ is also the radius.
∴ PO = OR = SO = OQ
∴ PO + OR = SO + OQ
∴ PR = SQ
Since, diagonals are equal.
Hence, we can conclude that PQRS is a rectangle.