Given that PQRS is a cyclic quadrilateral and also its diagonals bisect each other. What can you conclude about the quadrilateral?

Let PQRS be a cyclic quadrilateral.

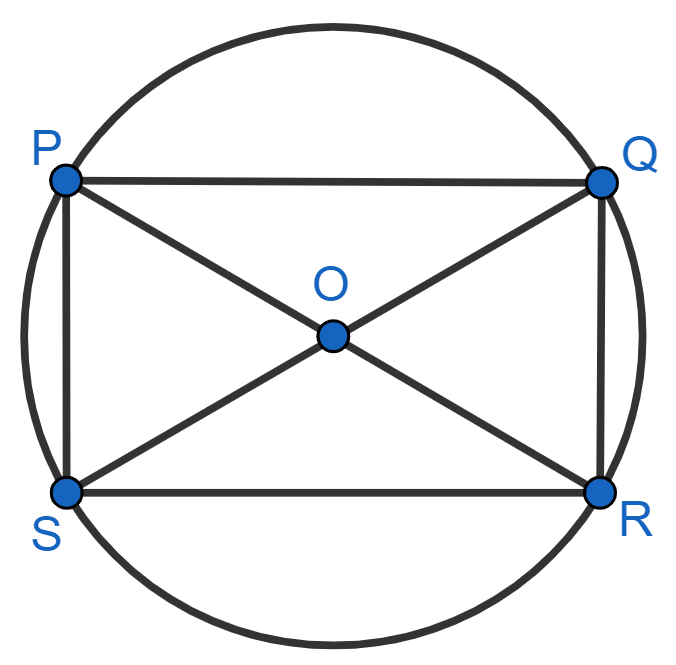
Given,

Diagonals bisect each other.

∴ PO = OR and SO = OQ.

From figure,

⇒ PO + OR = PR

⇒ PO + PO = PR

⇒ 2PO = PR

Since, PR is the diameter of the circle.

So, we can say that PO is the radius of the circle and OR is also the radius.

From figure,

⇒ SO + OQ = SQ

⇒ SO + SO = SQ

⇒ 2SO = SQ

Since, SQ is the diameter of the circle.

So, we can say that SO is the radius of the circle and OQ is also the radius.

∴ PO = OR = SO = OQ

∴ PO + OR = SO + OQ

∴ PR = SQ

Since, diagonals are equal.

Hence, we can conclude that PQRS is a rectangle.