Mathematics
Answer
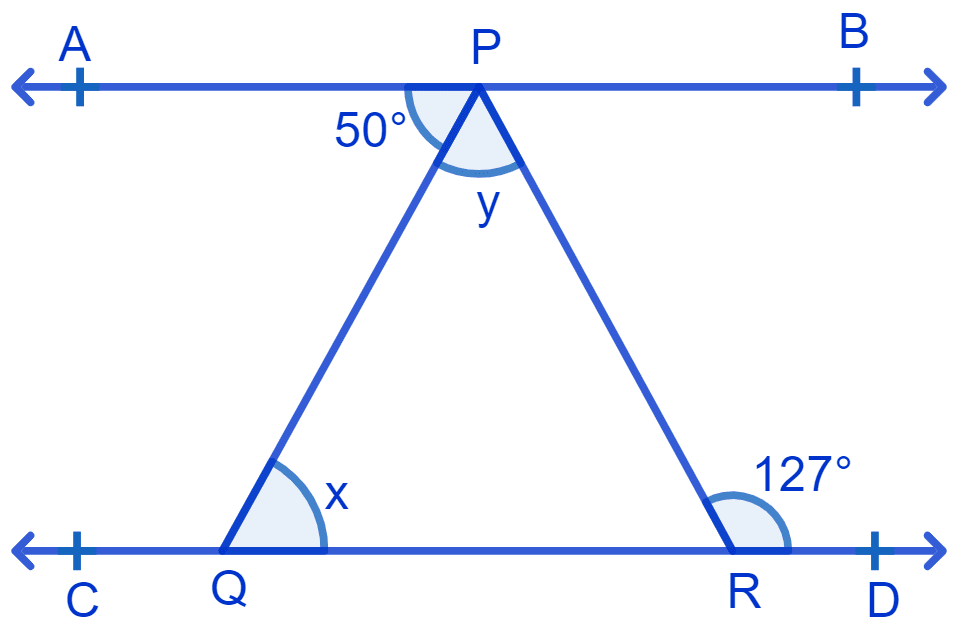
Given : ∠APQ = 50° and ∠PRD = 127°.
From figure,
PQ is the transversal.
⇒ ∠PQR = ∠APQ (Alternate interior angles are equal)
⇒ x = 50°.
From figure,
⇒ ∠PRQ + ∠PRD = 180° [Linear pairs]
⇒ ∠PRQ + 127° = 180°
⇒ ∠PRQ = 180° - 127° = 53°.
By angle sum property of triangle :
⇒ ∠PQR + ∠QPR + ∠PRQ = 180°
⇒ x + y + 53° = 180°
⇒ 50° + y + 53° = 180°
⇒ y = 180° - 103°
⇒ y = 77°
Hence, x = 50° and y = 77°.
Related Questions
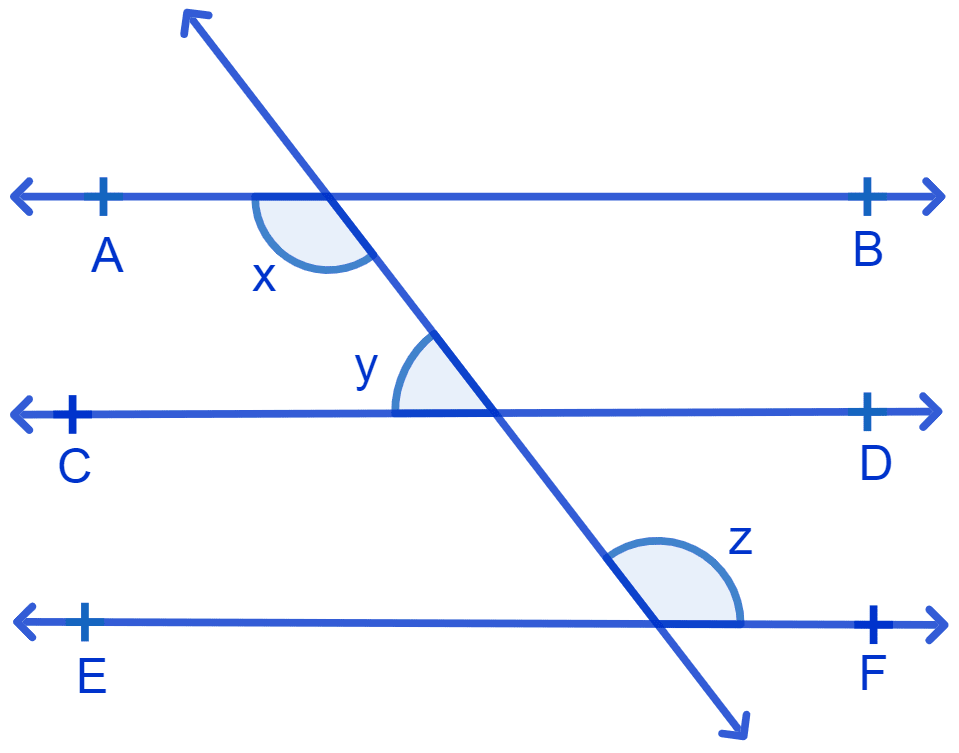
In Fig. if AB || CD, CD || EF and y : z = 3 : 7, find x.
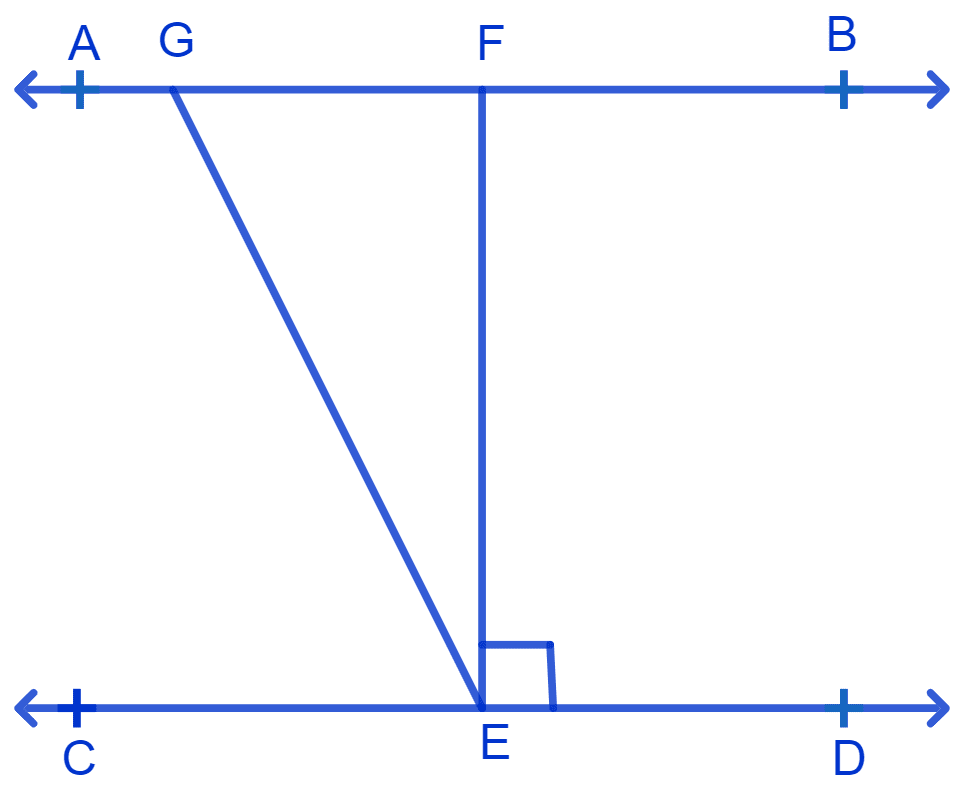
In Fig. if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
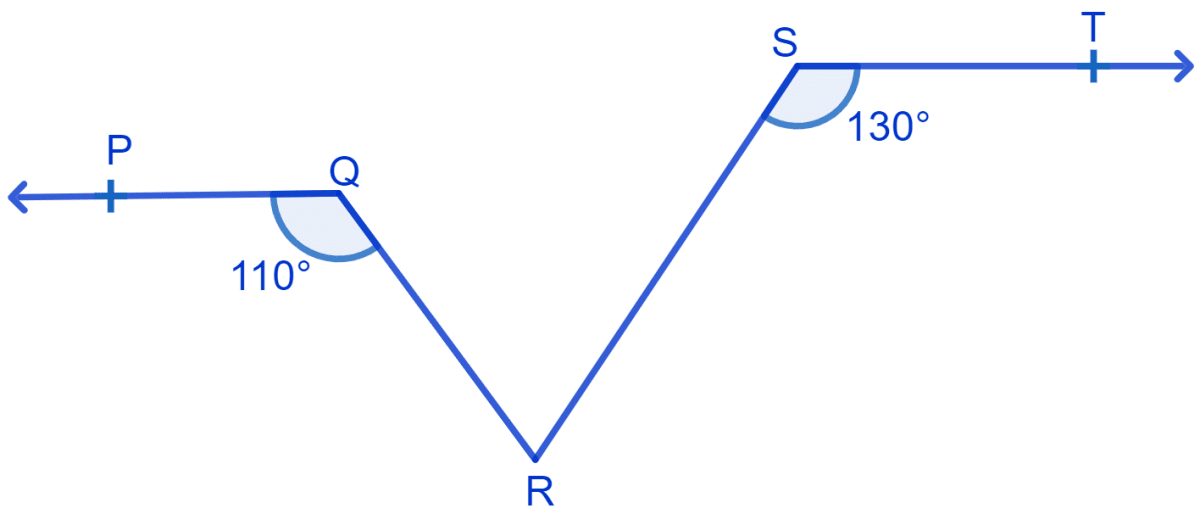
In Fig. if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
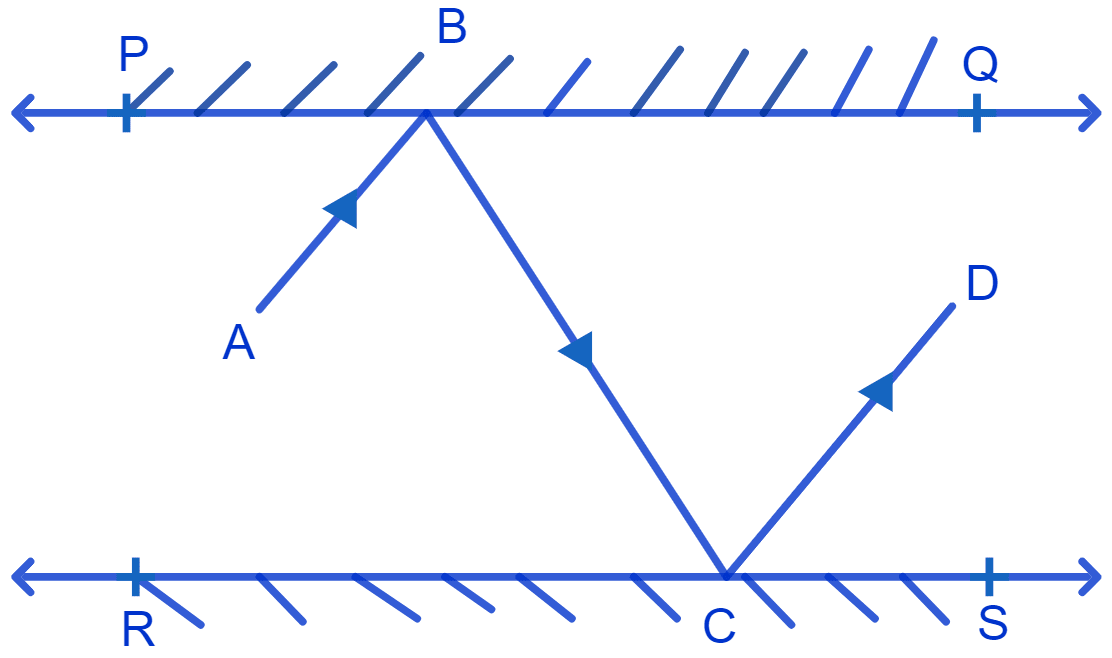
In Fig. PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.