Mathematics
In Fig. PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
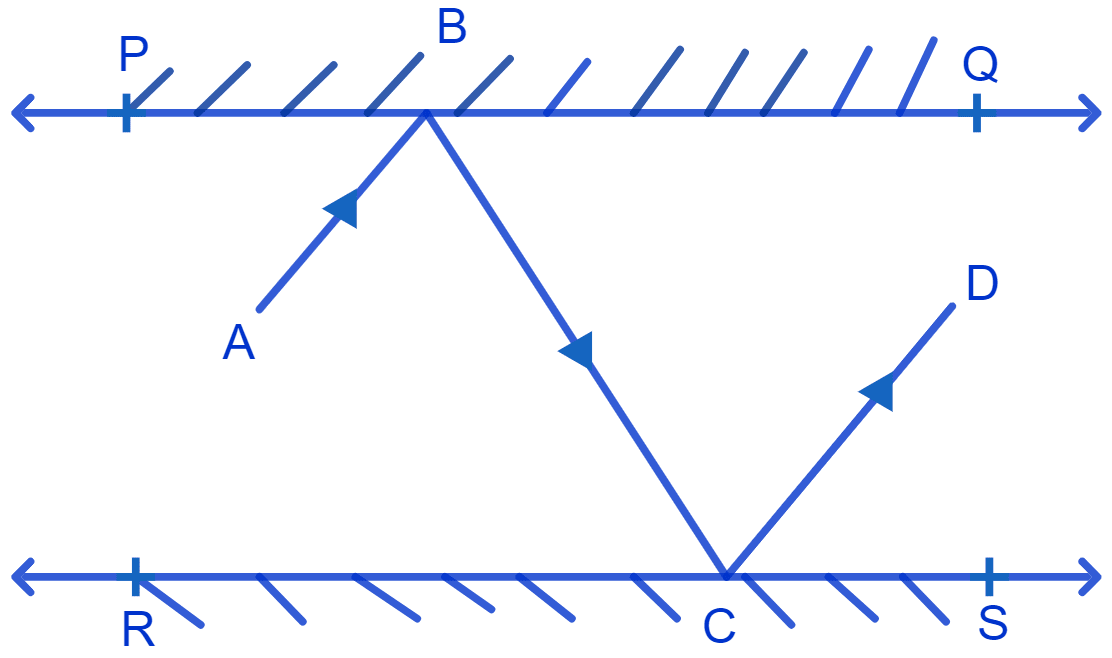
Lines & Angles
12 Likes
Answer
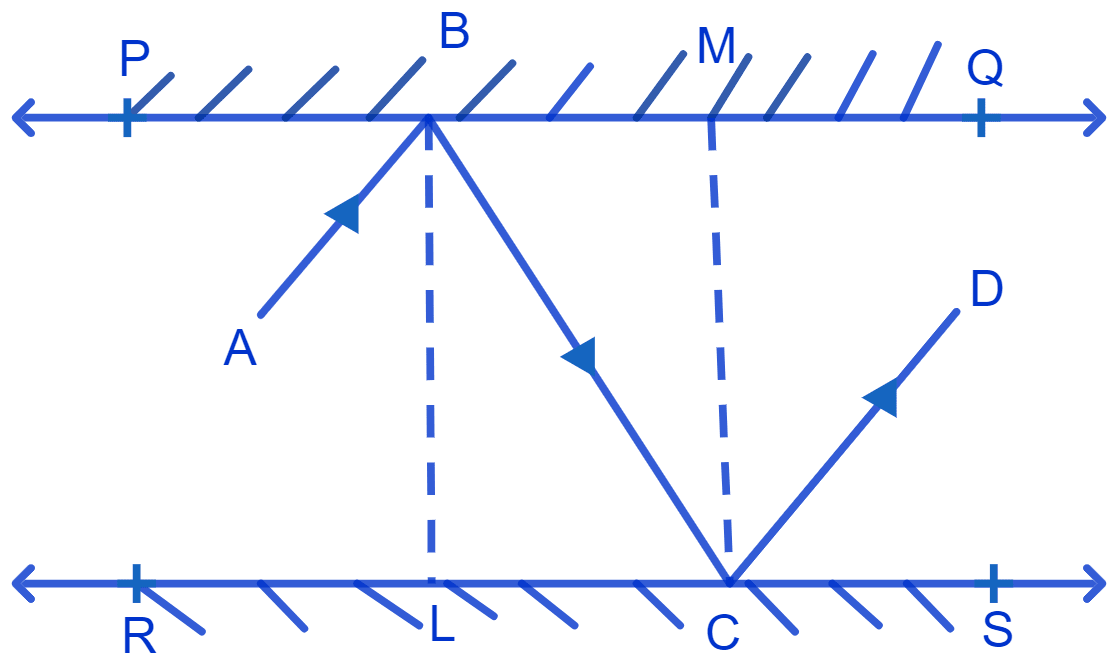
When two parallel lines are cut by a transversal, alternate angles formed are equal.
In optics the angle of incidence (the angle which an incident ray makes with a perpendicular to the surface at the point of incidence) and the angle of reflection (the angle formed by the reflected ray with a perpendicular to the surface at the point of incidence) are equal.
Draw a perpendicular line BL and CM at the point of incidence on both mirrors. Since PQ and RS are parallel to each other, perpendiculars drawn are also parallel i.e, BL || CM.
Since BC is a transversal to line BL and CM, alternate interior angles are equal.
∴ ∠LBC = ∠BCM = x …….(1)
By first law of reflection :
The angle of incidence (the angle which an incident ray makes with a perpendicular to the surface at the point of incidence) and the angle of reflection (the angle formed by the reflected ray with a perpendicular to the surface at the point of incidence) are equal.
By law of reflection, at the first point of incidence B on mirror PQ, we get :
⇒ ∠ABL = ∠LBC = x
⇒ ∠ABC = ∠ABL + ∠LBC
⇒ ∠ABC = x + x
⇒ ∠ABC = 2x ……(2)
By law of reflection, at the second point of incidence C on mirror RS, we get :
⇒ ∠MCD = ∠BCM = x
From figure,
⇒ ∠BCD = ∠BCM + ∠MCD
⇒ ∠BCD = x + x
⇒ ∠BCD = 2x …….(3)
From equation (2) and (3), we get ∠ABC = ∠BCD which are alternate interior angles for the lines AB and CD and BC as the transversal.
We know that, if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.
Since, alternate interior angles are equal, we can say AB is parallel to CD (AB || CD).
Hence, proved that AB || CD.
Answered By
6 Likes