Take your favourite proof and analyse it step-by-step along the lines discussed in Section A1.5 (what is given, what has been proved, what theorems and axioms have been used, and so on).

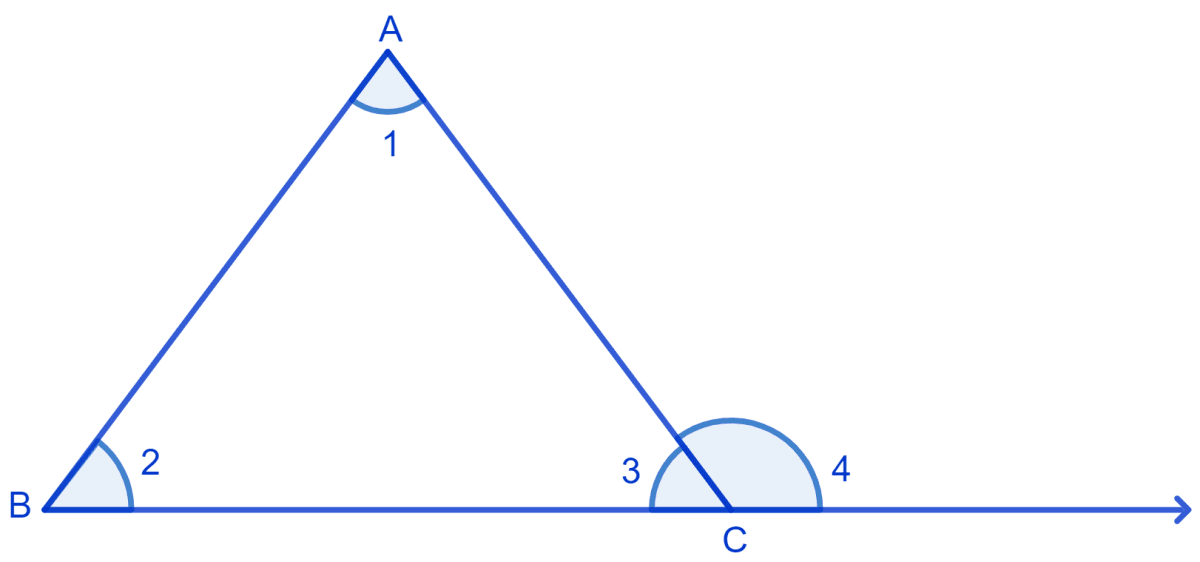
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

In Δ ABC,

⇒ ∠1 + ∠2 + ∠3 = 180° (By angle sum property) …..(1)

⇒ ∠3 + ∠4 = 180° (Linear pair) ….(2)

By comparing equation (1) and (2), we get :

⇒ ∠1 + ∠2 + ∠3 = ∠3 + ∠4

⇒ ∠1 + ∠2 = ∠4

Hence, proved that if a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.

Analysis of proof :

1. We begin with a triangle and one exterior angle.

2. Here we use angle sum property of triangle that is sum of three interior angles of a triangle is 180° to show ∠1 + ∠2 + ∠3 = 180°.(By theorem)

3. Here we use linear pair axiom, which states that the angles on a straight line add up to 180° to show that ∠3 + ∠4 = 180°.

4. Here we use Euclid's axiom which states that: “Things which are equal to the same thing are equal to each other.”

5. Here we use Euclid‟s axiom which states that: “If equals are subtracted from equals, the remainders are equal.”