Mathematics
Find counter-examples to disprove the following statements:
(i) If the corresponding angles in two triangles are equal, then the triangles are congruent.
(ii) A quadrilateral with all sides equal is a square.
(iii) A quadrilateral with all angles equal is a square.
(iv) For integers a and b, = a + b
(v) 2n2 + 11 is a prime for all whole numbers n.
(vi) n2 – n + 41 is a prime for all positive integers n.
Mathematics Proofs
2 Likes
Answer
(i) Counter example :
Consider two equilateral triangle Δ ABC and Δ DEF of length 3 cm and 6 cm respectively.
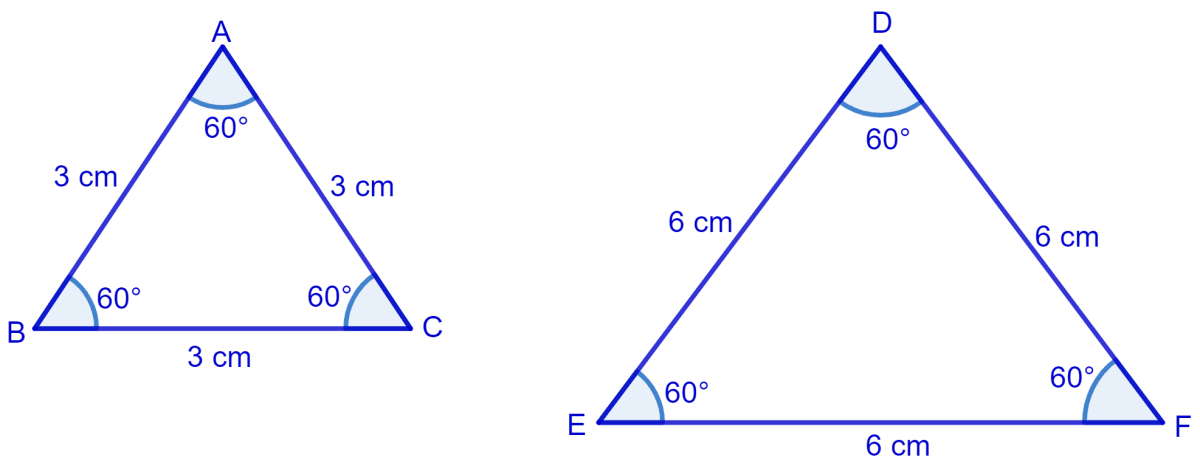
From figure,
All corresponding angles are same but sides are of different length.
∴ Δ ABC and Δ DEF are not congruent.
(ii) Counter example :
A quadrilateral with all sides equal is a rhombus which may not be a square.
(iii) Counter example :
A rectangle has all angles equal, but may not be a square.
(iv) Given,
Equation : = a + b
Counter example : Let a = 3 and b = 4
Substituting value of a and b in L.H.S. of the equation, we get :
Substituting value of a and b in R.H.S. of the equation, we get :
⇒ 3 + 4 = 7.
Since,
L.H.S. ≠ R.H.S.
Hence, for a = 3 and b = 4, the statement = a + b is not true.
(v) Given,
Equation : 2n2 + 11
Counter example :
Let n = 11 (by hit and trial method)
Substituting value of n in given equation.
2n2 + 11 = 2(11)2 + 11
= 2 x 121 + 11
= 242 + 11 = 253.
253 is divisible by 11.
Therefore, 253 is not a prime number so given statement is false for n = 11.
Hence, for n = 11, 2n2 + 11 = 253, which is not a prime number.
(vi) Given,
Equation : n2 - n + 41
Counter example :
Let n = 41.
Substituting value of n in given equation, we get :
n2 - n + 41 = (41)2 - 41 + 41
= 1681.
1681 is not prime.
Hence, for n = 41, n2 – n + 41 is not prime.
Answered By
1 Like
Related Questions
Look at the following pattern :
12 = 1
112 = 121
1112 = 12321
11112 = 1234321
111112 = 123454321
Make a conjecture about each of the following:
1111112 =
11111112 =
Check if your conjecture is true.
List five axioms (postulates) used in this book.
Take your favourite proof and analyse it step-by-step along the lines discussed in Section A1.5 (what is given, what has been proved, what theorems and axioms have been used, and so on).
Prove that the sum of two odd numbers is even.