Mathematics
Look at the following pattern :
12 = 1
112 = 121
1112 = 12321
11112 = 1234321
111112 = 123454321
Make a conjecture about each of the following:
1111112 =
11111112 =
Check if your conjecture is true.
Mathematics Proofs
3 Likes
Answer
Looking at above pattern,
Possible conjecture :
The resultant will be series of numbers from one till number of 1's in the digit to be squared and then reversing the order.
By following conjecture, we can write:
⇒ 1111112 = 12345654321 and
⇒ 11111112 = 1234567654321
On actual multiplication, we get :
⇒ 1111112 = 12345654321 and
⇒ 11111112 = 1234567654321.
Hence, conjecture is true.
Answered By
3 Likes
Related Questions
Go back to Pascal’s triangle.
Line 1 : 1 = 110
Line 2 : 1 1 = 111
Line 3 : 1 2 1 = 112
Make a conjecture about Line 4 and Line 5. Does your conjecture hold? Does your conjecture hold for Line 6 too?
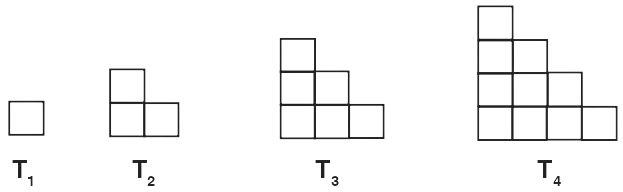
Let us look at the triangular numbers figure again. Add two consecutive triangular numbers. For example, T1 + T2 = 4, T2 + T3 = 9, T3 + T4 = 16.
What about T4 + T5 ? Make a conjecture about Tn-1 + Tn.
List five axioms (postulates) used in this book.
Find counter-examples to disprove the following statements:
(i) If the corresponding angles in two triangles are equal, then the triangles are congruent.
(ii) A quadrilateral with all sides equal is a square.
(iii) A quadrilateral with all angles equal is a square.
(iv) For integers a and b, = a + b
(v) 2n2 + 11 is a prime for all whole numbers n.
(vi) n2 – n + 41 is a prime for all positive integers n.