Mathematics
In the adjoining figure, O is the centre of a circle and PQ is a chord. If the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is
100°
80°
90°
75°

Answer
∵ radius of a circle and tangent through that point are perpendicular to each other.
∴ ∠OPR = 90°.
From figure,
⇒ ∠OPR = ∠RPQ + ∠OPQ
⇒ 90° = 50° + ∠OPQ
⇒ ∠OPQ = 90° - 50° = 40°.
OP = OQ (Radius of the circle.)
Hence, △OPQ is an isosceles triangle with ∠OQP = ∠OPQ = 40°.
Since, sum of angles of a triangle = 180°.
In △OPQ,
⇒ ∠OPQ + ∠OQP + ∠POQ = 180°
⇒ 40° + 40° + ∠POQ = 180°
⇒ 80° + ∠POQ = 180°
⇒ ∠POQ = 180° - 80°
⇒ ∠POQ = 100°.
Hence, Option 1 is the correct option.
Related Questions
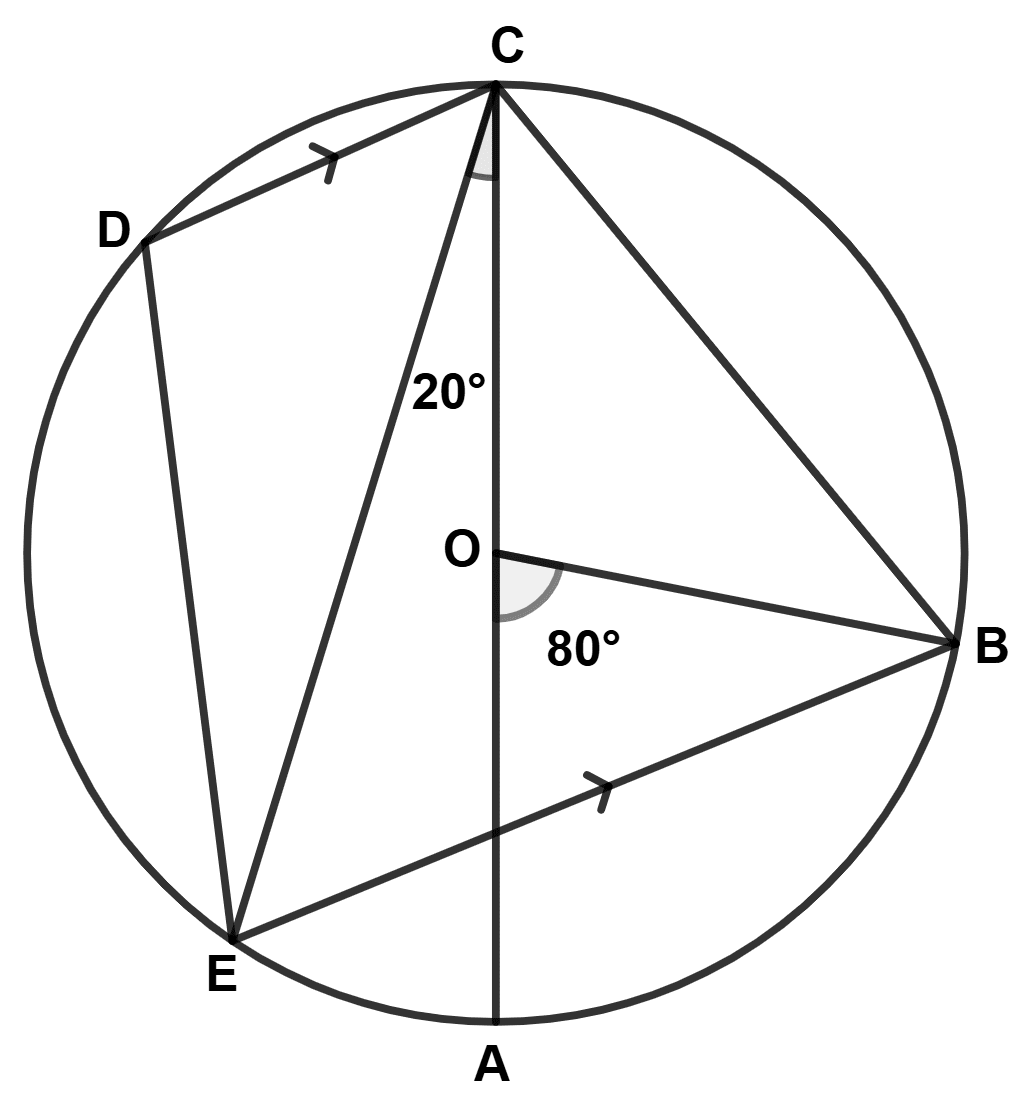
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
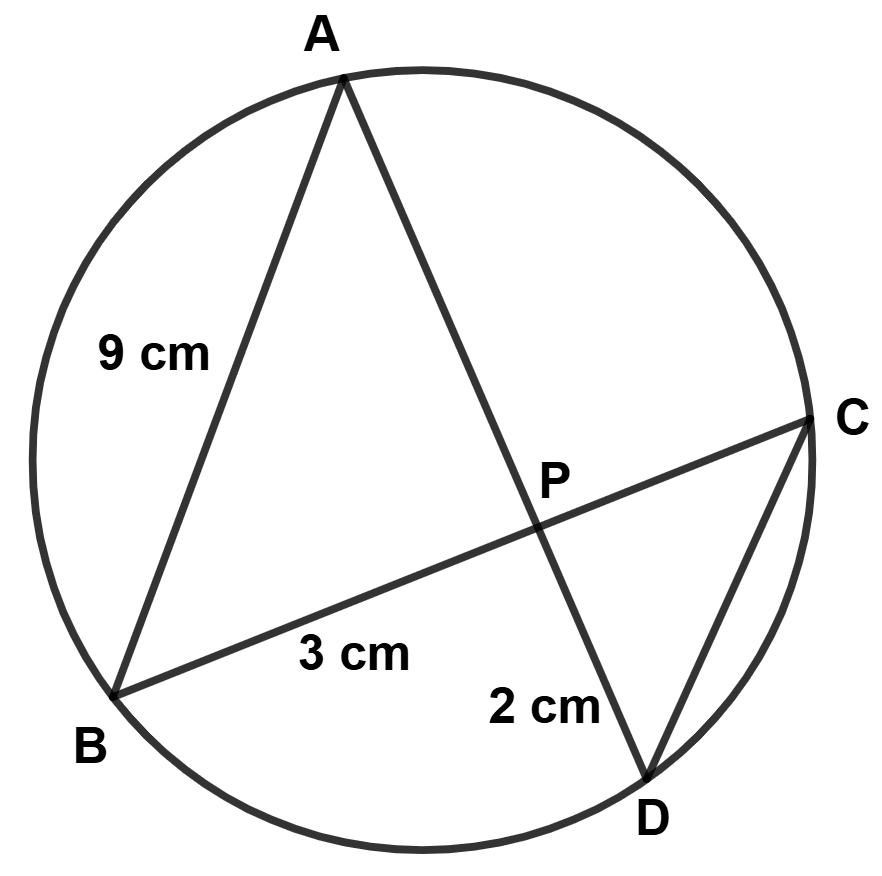
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
(a) Prove that △ APB ~ △ CPD
(b) Find the length of CD
(c) Find area △ APB : area △ CPD.
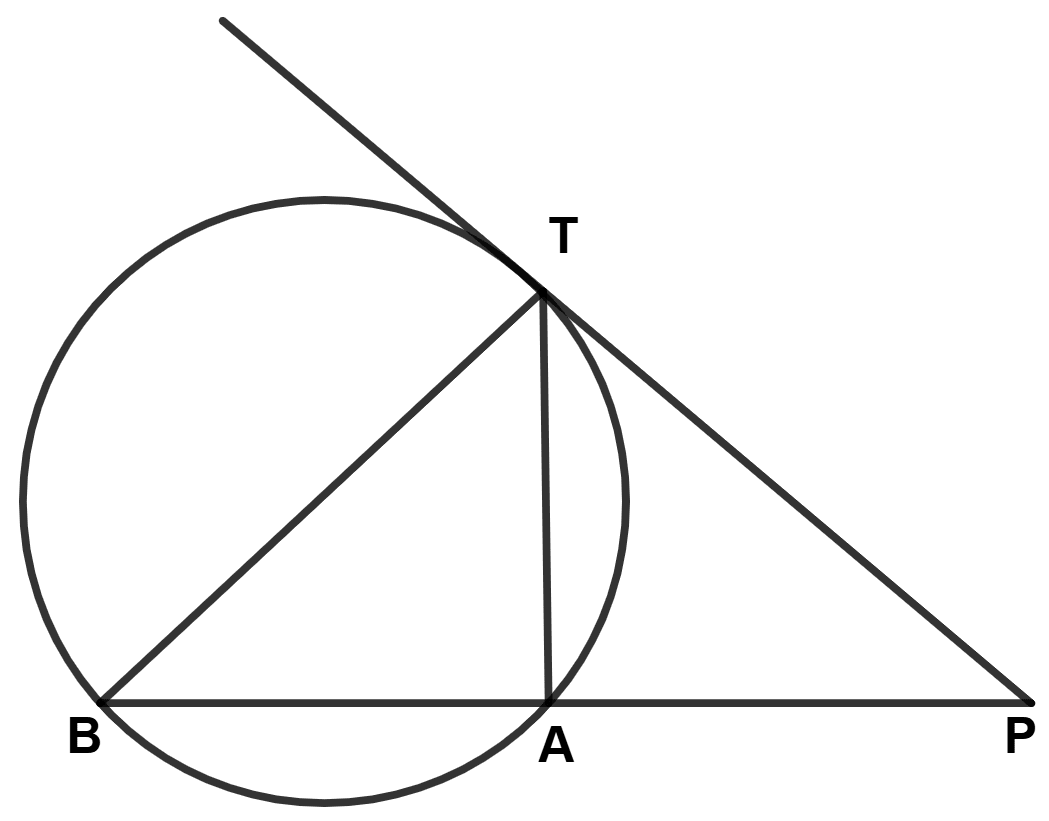
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P. Given PT = 20 cm and PA = 16 cm.
(a) Prove △ PTB ~ △ PAT
(b) Find the length of AB.
Prove that any four vertices of a regular pentagon are concyclic.