Mathematics
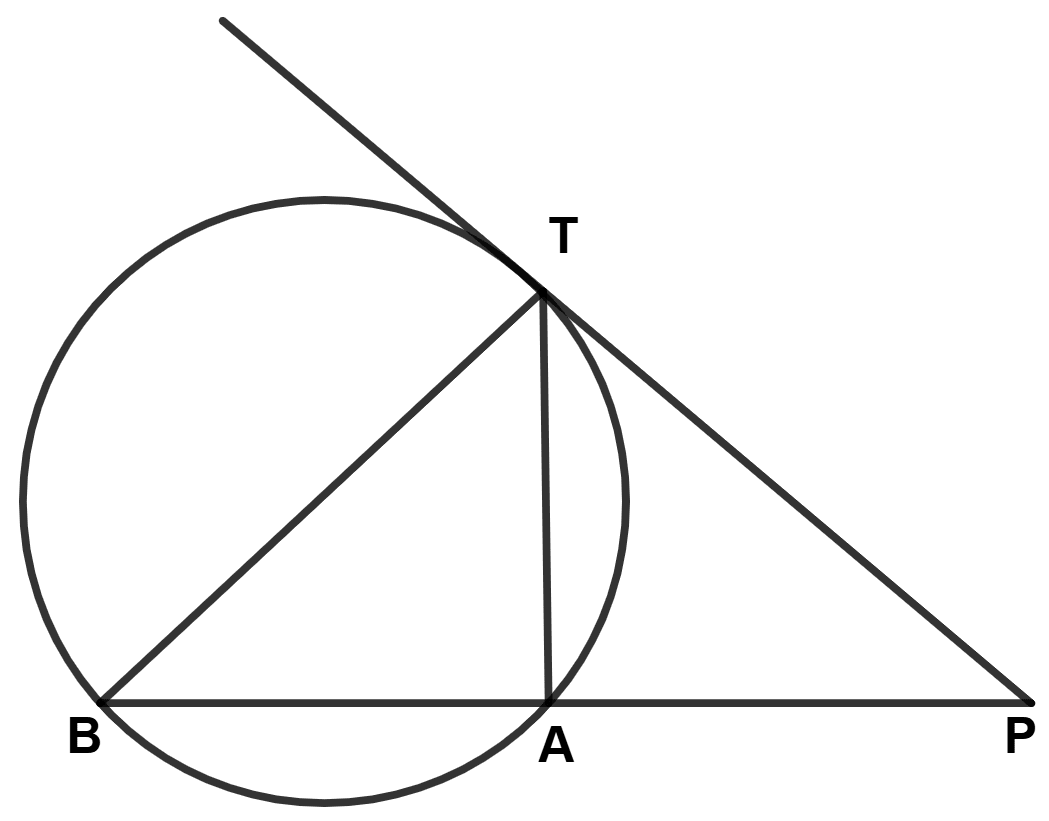
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P. Given PT = 20 cm and PA = 16 cm.
(a) Prove △ PTB ~ △ PAT
(b) Find the length of AB.
Similarity
ICSE Sp 2025
23 Likes
Answer
(a) In △ PTB and △ PAT,
⇒ ∠PTA = ∠PBT (Alternate segment theorem)
⇒ ∠TPA = ∠BPT (Common angle)
∴ △ PTB ~ △ PAT (By A.A. axiom)
Hence, proved that △ PTB ~ △ PAT.
(b) We know that,
If a chord and a tangent intersect externally, then the product of the lengths of segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
⇒ PA × PB = PT2
⇒ PA × (PA + AB) = PT2
⇒ 16 × (16 + AB) = 202
⇒ 16 × (16 + AB) = 400
⇒ 16 + AB = 25
⇒ AB = 25 - 16 = 9 cm.
Hence, AB = 9 cm.
Answered By
10 Likes
Related Questions
Using step-deviation method, find mean for the following frequency distribution
Class Frequency 0-15 3 15-30 4 30-45 7 45-60 6 60-75 8 75-90 2 Find the coordinates of the centroid P of the △ ABC, whose vertices are A(-1, 3), B(3, -1) and C(0, 0). Hence, find the equation of a line passing through P and parallel to AB.
The following bill shows the GST rate and the marked price of articles :
Rajdhani Departmental Store
S.No. Item Marked price Discount Rate of GST (a) Dry fruits (1 kg) ₹ 1200 ₹ 100 12% (b) Packed Wheat Flour (5 kg) ₹ 286 Nil 5% (c) Bakery Products ₹ 500 10% 12% Find the total amount to be paid (including GST) for the above bill.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.