Mathematics
Prove that any four vertices of a regular pentagon are concyclic.
Circles
1 Like
Answer
Let the regular pentagon be ABCDE.
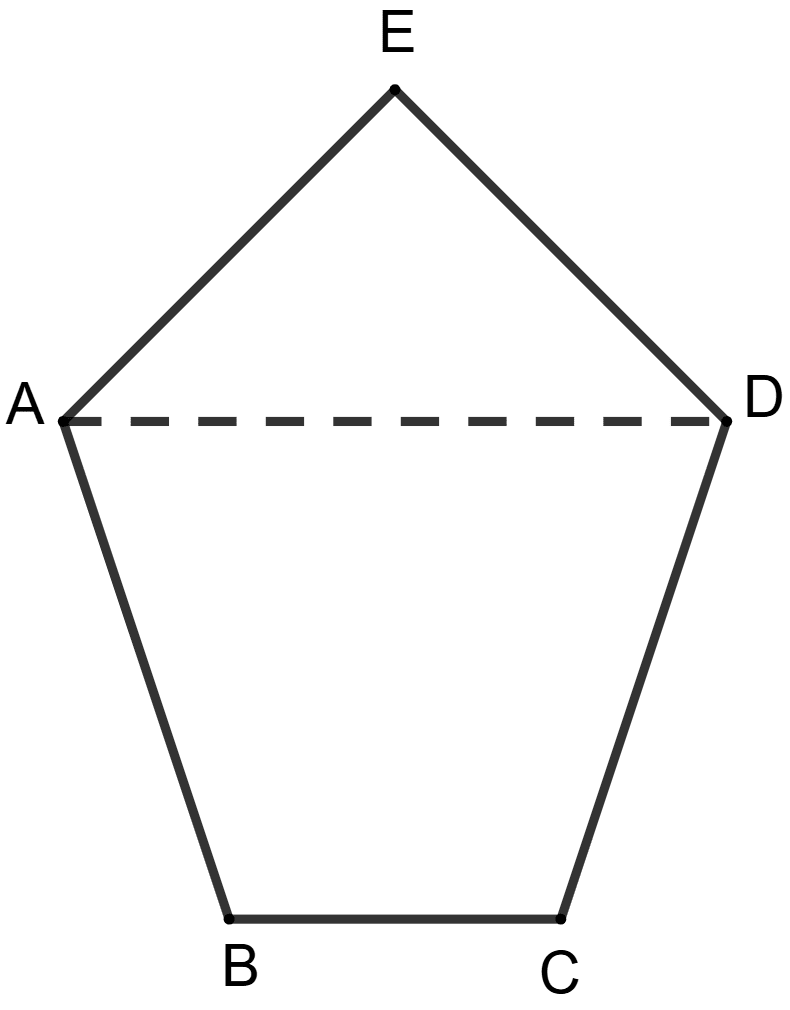
Since it's regular, and all interior angles are equal to 108°.
∴ ∠ABC = ∠BCD = ∠CDE = ∠DEA = ∠EAB
Interior angle of a regular polygon is given by :
So, each interior angle of a regular pentagon = - 108°.
In triangle AED,
AE = ED [Sides of a regular pentagon are equal]
∴ ∠EAD = ∠EDA [Angles opposite to equal sides are equal] ……(1)
⇒ ∠AED + ∠EAD + ∠EDA = 180°
⇒ 108° + ∠EAD + ∠EAD = 180°
⇒ 2∠EAD = 180° - 108°
⇒ 2∠EAD = 72°
⇒ ∠EAD =
⇒ ∠EAD = 36°
∴ ∠EDA = 36°.
From figure,
⇒ ∠BAD = ∠BAE - ∠EAD = 108° - 36° = 72°.
In quadrilateral ABCD,
∠BAD + ∠BCD = 72° + 108° = 180°.
Since, sum of opposite angles = 180°,
which is possible when the quadrilateral is cyclic quadrilateral.
Hence, proved that any four vertices of a regular pentagon are concylic.
Answered By
1 Like
Related Questions
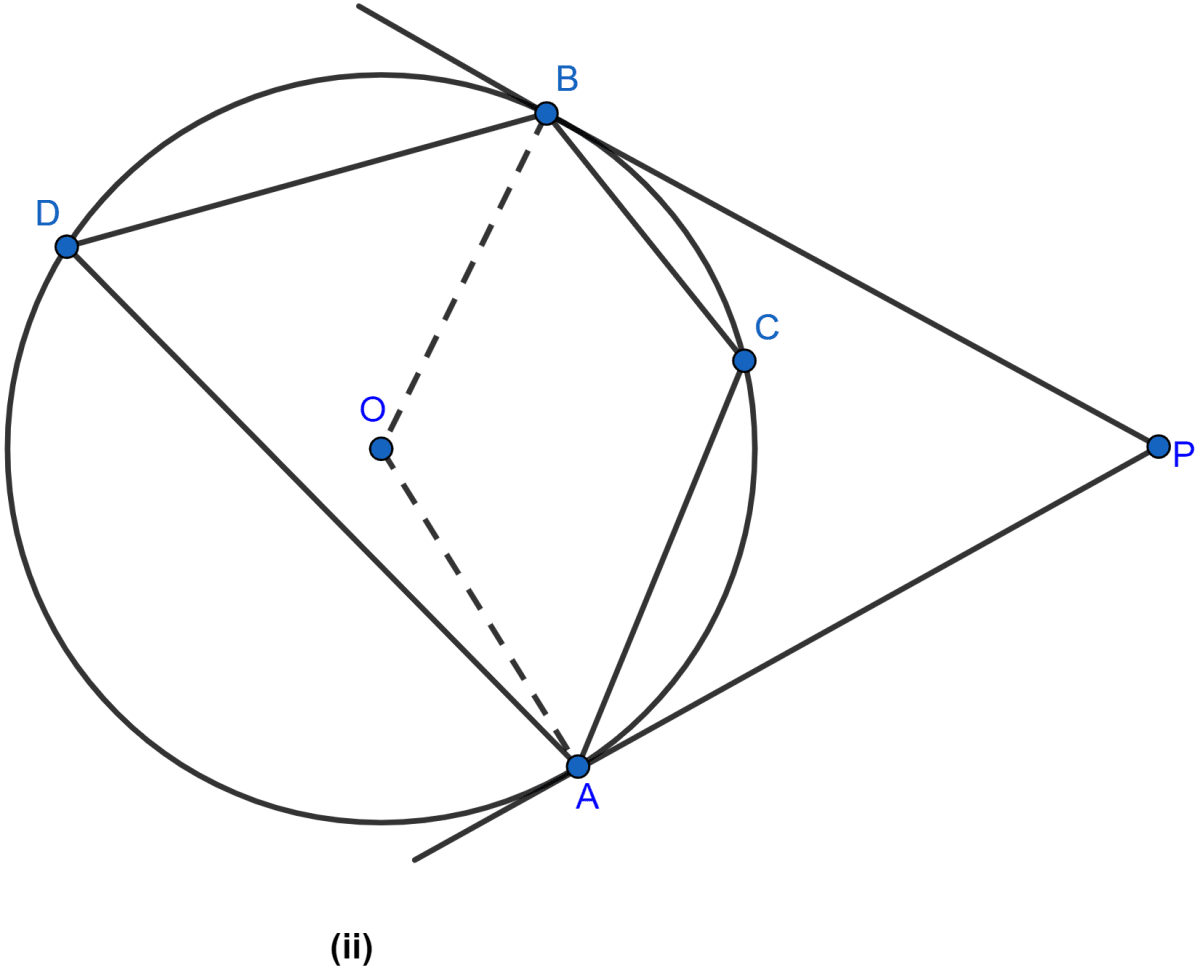
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find
(i) ∠ADB
(ii) ∠AOB
(iii) ∠ACB
(iv) ∠APB.
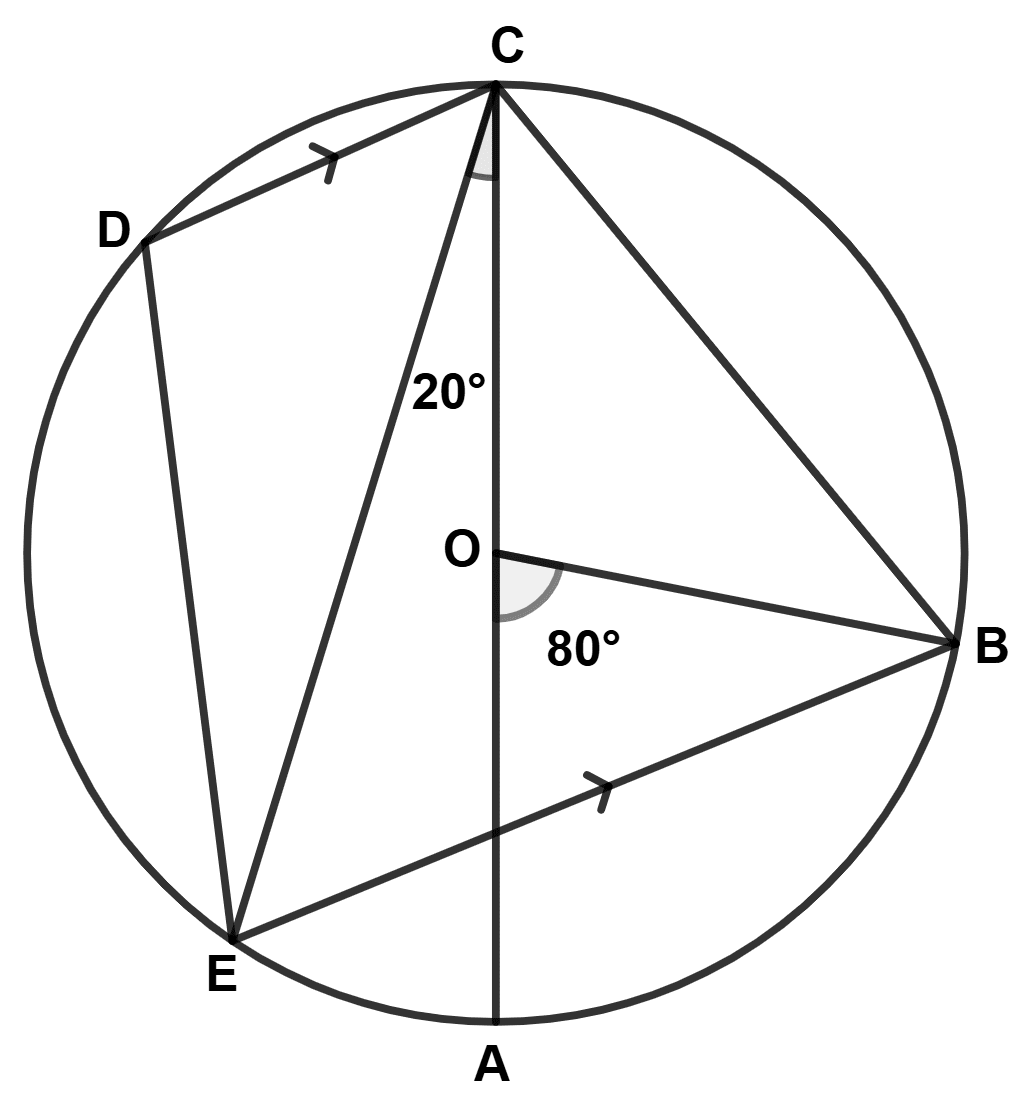
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
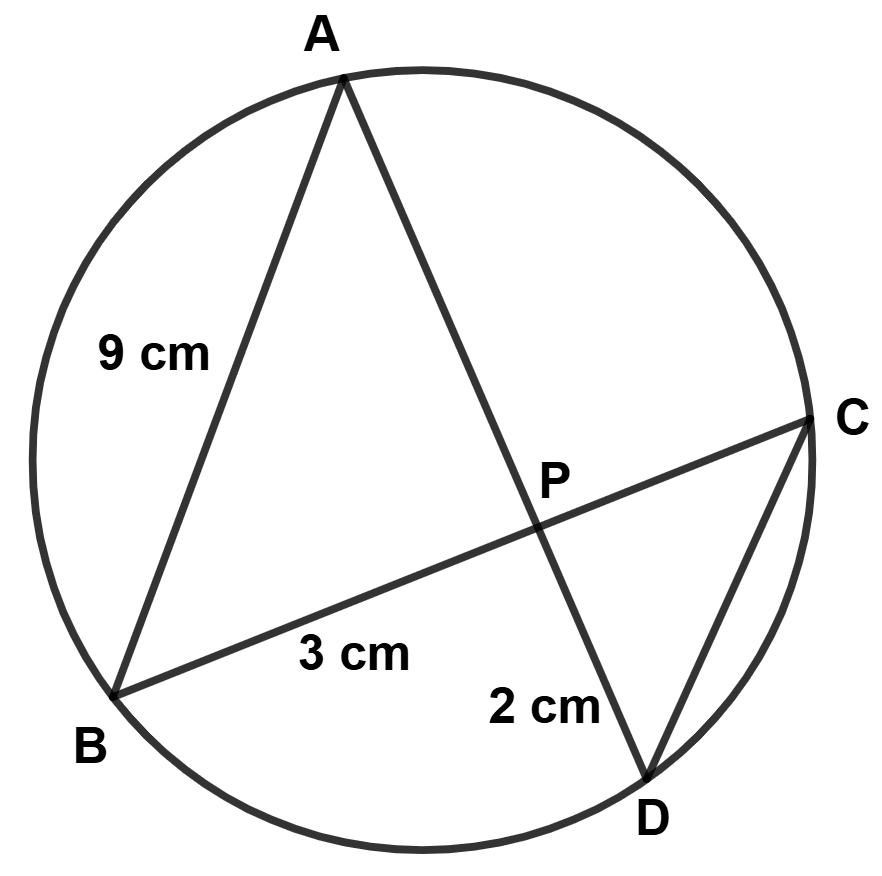
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
(a) Prove that △ APB ~ △ CPD
(b) Find the length of CD
(c) Find area △ APB : area △ CPD.
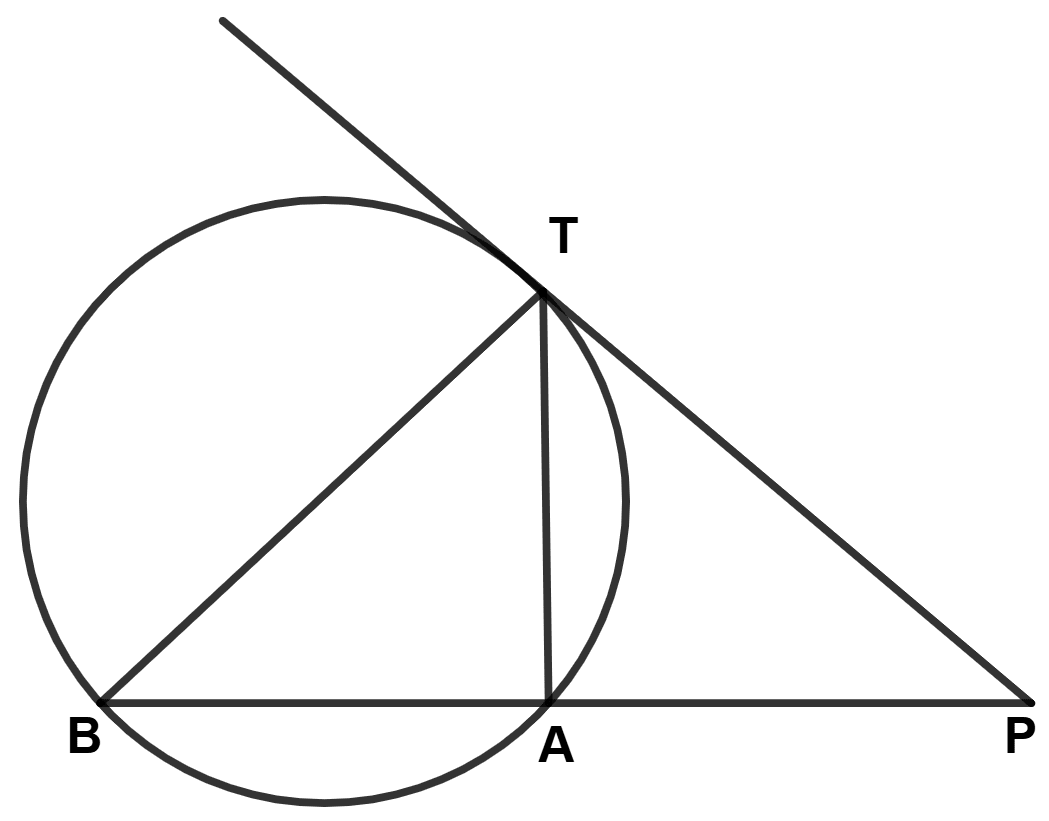
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P. Given PT = 20 cm and PA = 16 cm.
(a) Prove △ PTB ~ △ PAT
(b) Find the length of AB.