Mathematics
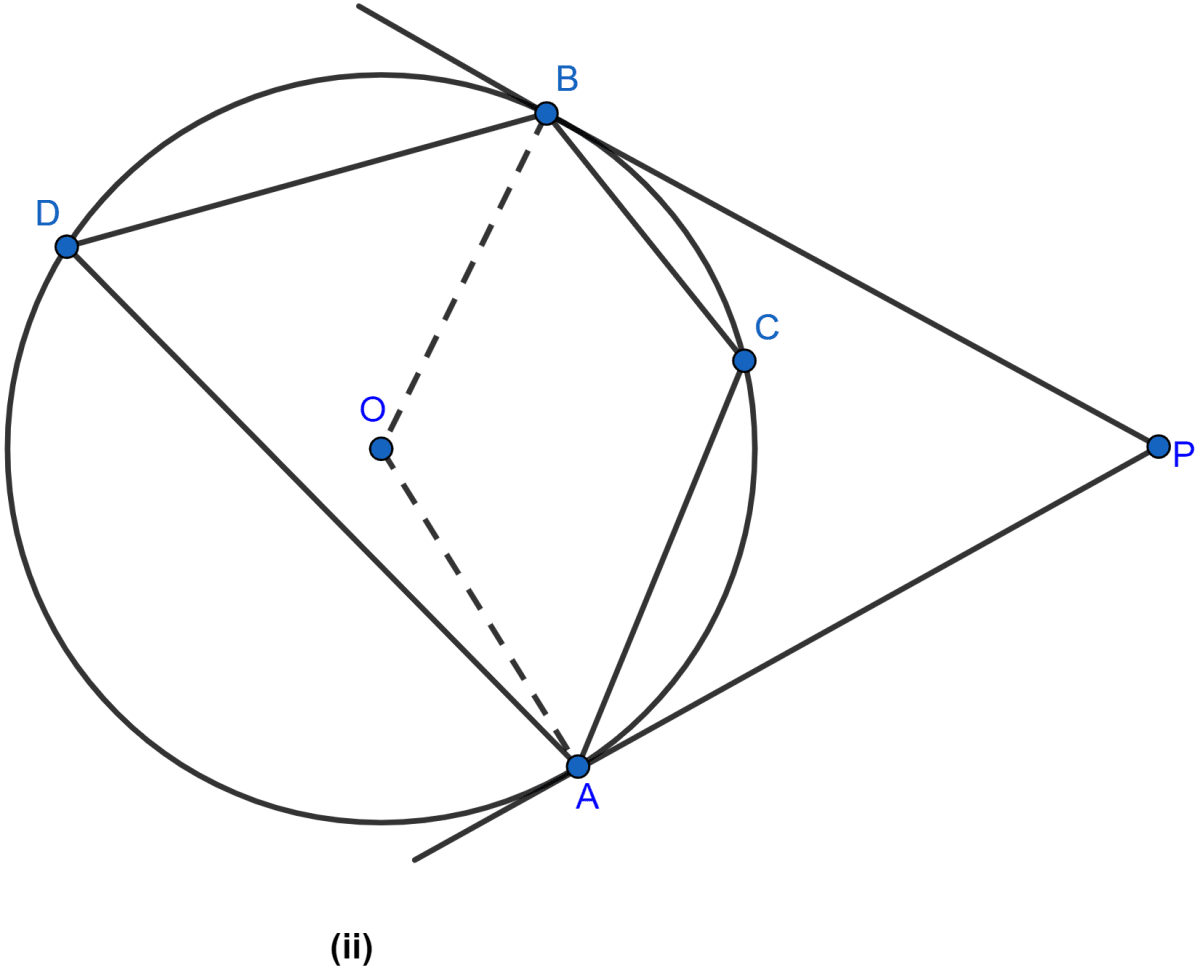
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find
(i) ∠ADB
(ii) ∠AOB
(iii) ∠ACB
(iv) ∠APB.
Circles
44 Likes
Answer
(i) ∠CDB = ∠CBP (∵ angles in alternate segments are equal.)
∴ ∠CDB = 25° ….(i)
Similarly, ∠CDA = ∠CAP = 40° (∵ angles in alternate segments are equal.)
∴ ∠ADB = ∠CDA + ∠CDB = 40° + 25° = 65°.
Hence, the value of ∠ADB = 65°.
(ii) Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
⇒ ∠AOB = 2∠ADB (As angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ ∠AOB = 2 × 65°
⇒ ∠AOB = 130°.
Hence, the value of ∠AOB = 130°.
(iii) ACBD is a cyclic quadrilateral.
∴ ∠ACB + ∠ADB = 180° (∵ sum of opposite angles = 180°.)
⇒ ∠ACB + 65° = 180°
⇒ ∠ACB = 180° - 65° = 115°.
Hence, the value of ∠ACB = 115°.
(iv) From figure,
⇒ ∠AOB + ∠APB = 180°
⇒ 130° + ∠APB = 180°
⇒ ∠APB = 180° - 130° = 50°.
Hence, the value of ∠APB = 50°.
Answered By
26 Likes
Related Questions
In the figure (i) given below, chords AB, BC and CD of a circle with center O are equal. If ∠BCD = 120°, find
(i) ∠BDC
(ii) ∠BEC
(iii) ∠AEB
(iv) ∠AOB.
Hence, prove that △OAB is equilateral.

In the figure (i) given below, AB and XY are diameters of a circle with centre O. If ∠APX = 30°, find
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX.

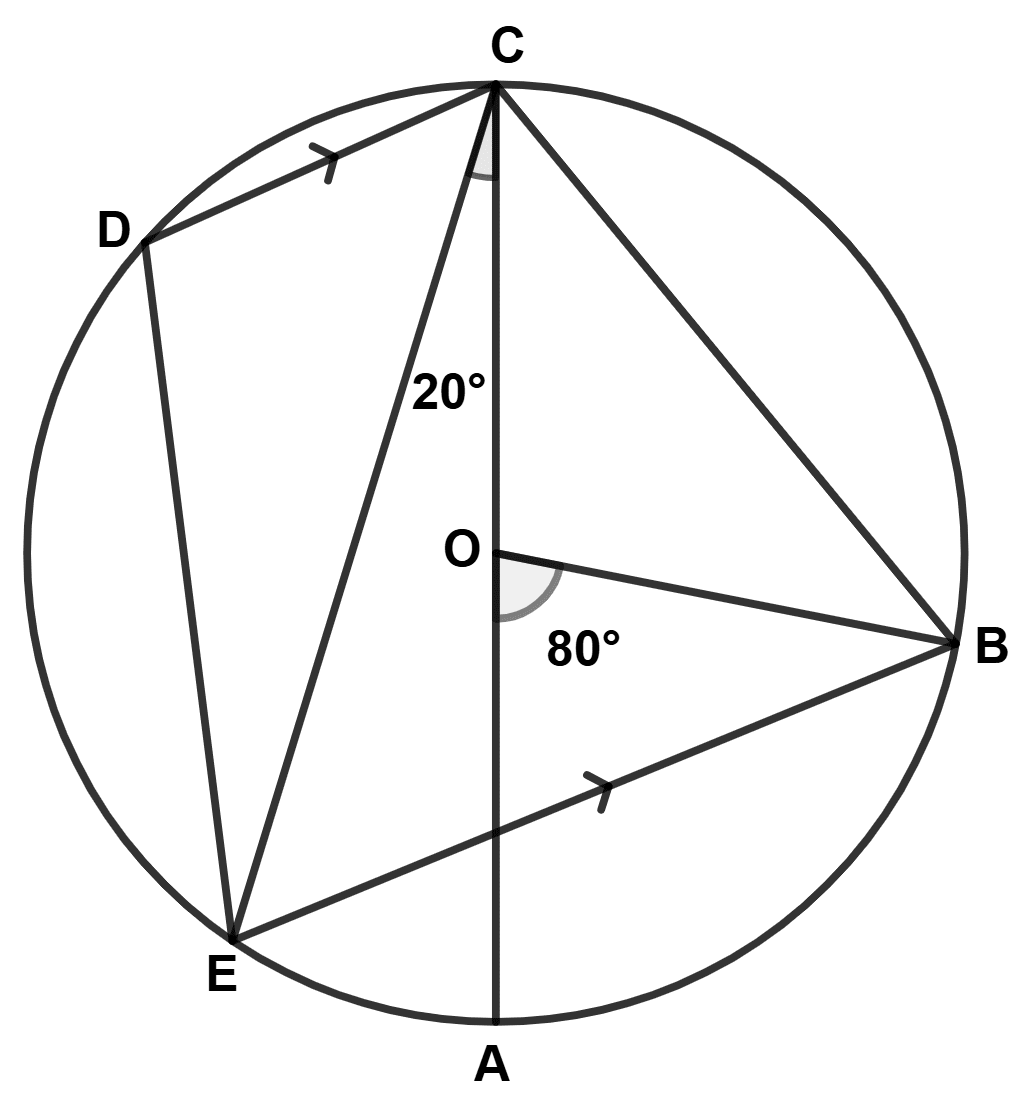
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
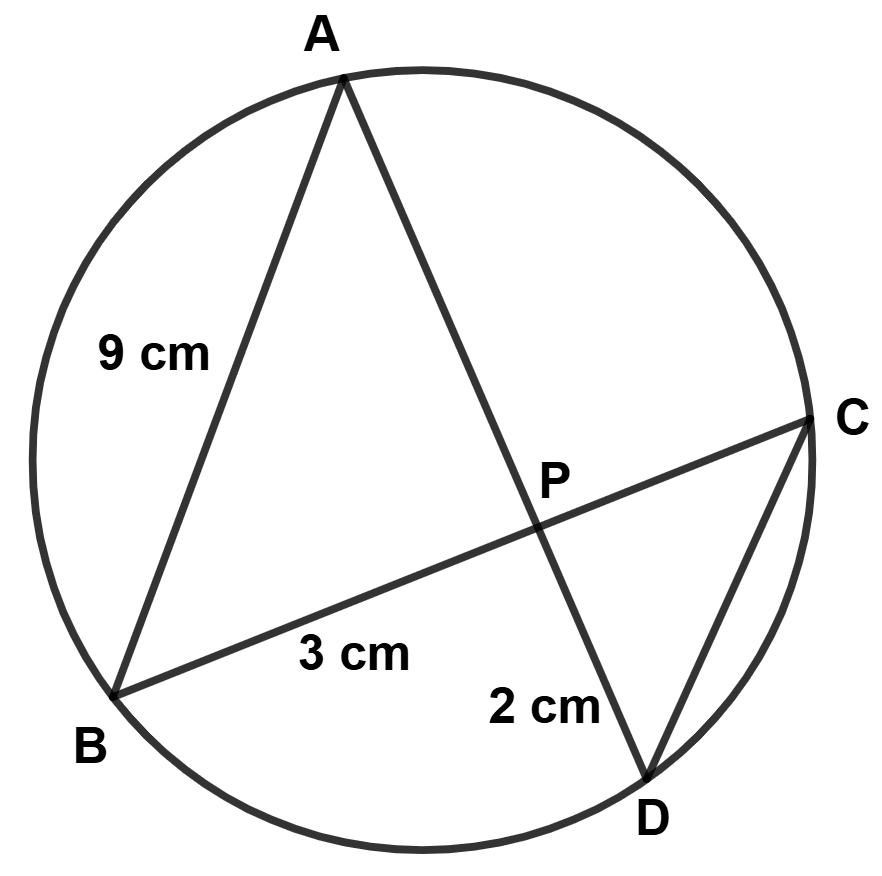
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
(a) Prove that △ APB ~ △ CPD
(b) Find the length of CD
(c) Find area △ APB : area △ CPD.