Solving (simple) Problems (Based on Quadratic Equations)

The sum of two natural numbers is 5 and the sum of their reciprocals is $\dfrac{5}{6}$, the numbers are :

1. 2 and 5

2. 4 and 2

3. 2 and 3

4. 3 and 4

Answer

Let two natural numbers be x and y.

Given,

Sum = 5

⇒ x + y = 5

⇒ x = 5 - y ........(1)

Sum of reciprocals = $\dfrac{5}{6}$

⇒ $\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{5}{6}$ ...........(2)

Substituting value of x from equation (1) in (2) :

$\Rightarrow \dfrac{1}{5 - y} + \dfrac{1}{y} = \dfrac{5}{6} \\[1em] \Rightarrow \dfrac{y + 5 - y}{y(5 - y)} = \dfrac{5}{6} \\[1em] \Rightarrow \dfrac{5}{5y - y^2} = \dfrac{5}{6} \\[1em] \Rightarrow 5y - y^2 = \dfrac{6 \times 5}{5} \\[1em] \Rightarrow 5y - y^2 = 6 \\[1em] \Rightarrow y^2 - 5y + 6 = 0 \\[1em] \Rightarrow y^2 - 2y - 3y + 6 = 0 \\[1em] \Rightarrow y(y - 2) - 3(y - 2) = 0 \\[1em] \Rightarrow (y - 3)(y - 2) = 0 \\[1em] \Rightarrow y - 3 = 0 \text{ or } y - 2 = 0 \\[1em] \Rightarrow y = 3 \text{ or } y = 2.$

If y = 3,

x = 5 - y = 5 - 3 = 2.

If y = 2,

x = 5 - y = 5 - 2 = 3.

∴ Numbers are 2 and 3.

Hence, Option 3 is the correct option.

The product of two consecutive even whole numbers is 24, the numbers are :

1. -8 and -3

2. 3 and 8

3. -4 and -6

4. 4 and 6

Answer

Let two consecutive even whole numbers be x and x + 2.

Given,

Product of two consecutive even whole numbers = 24.

∴ x(x + 2) = 24

⇒ x² + 2x = 24

⇒ x² + 2x - 24 = 0

⇒ x² + 6x - 4x - 24 = 0

⇒ x(x + 6) - 4(x + 6) = 0

⇒ (x - 4)(x + 6) = 0

⇒ x - 4 = 0 or x + 6 = 0

⇒ x = 4 or x = -6.

Since, x is a whole number so x cannot be equal to -6.

x = 4 and x + 2 = 6.

Hence, Option 4 is the correct option.

The sum of the squares of two consecutive integers is 41. The integers are :

1. 4 and -5 or -4 and 5

2. 4 and 5 or -4 and -5

3. 3 and 4 or -4 and -3

4. 6 and 3 or -6 and -3

Answer

Let two consecutive integers be x and x + 1.

Given,

Sum of squares of two consecutive integers = 41.

⇒ x² + (x + 1)² = 41

⇒ x² + x² + 1 + 2x = 41

⇒ 2x² + 2x = 41 - 1

⇒ 2x² + 2x = 40

⇒ 2(x² + x) = 40

⇒ x² + x = $\dfrac{40}{2}$

⇒ x² + x = 20

⇒ x² + x - 20 = 0

⇒ x² + 5x - 4x - 20 = 0

⇒ x(x + 5) - 4(x + 5) = 0

⇒ (x - 4)(x + 5) = 0

⇒ x - 4 = 0 or x + 5 = 0

⇒ x = 4 or x = -5

If x = 4,

⇒ x + 1 = 4 + 1 = 5.

If x = -5,

⇒ x + 1 = -5 + 1 = -4.

Numbers = 4 and 5 or -4 and -5.

Hence, Option 2 is the correct option.

The sum of a number and its reciprocal is 5.2. The number is

1. 5 or $\dfrac{1}{5}$

2. 2 or $\dfrac{1}{2}$

3. 4 or $\dfrac{1}{4}$

4. -2 or $-\dfrac{1}{2}$

Answer

Let number be x.

Given,

Sum of a number and its reciprocal is 5.2

$\Rightarrow x + \dfrac{1}{x} = 5.2 \\[1em] \Rightarrow \dfrac{x^2 + 1}{x} = \dfrac{52}{10} \\[1em] \Rightarrow 10(x^2 + 1) = 52x \\[1em] \Rightarrow 10x^2 + 10 = 52x \\[1em] \Rightarrow 10x^2 - 52x + 10 = 0 \\[1em] \Rightarrow 10x^2 - 50x - 2x + 10 = 0 \\[1em] \Rightarrow 10x(x - 5) - 2(x - 5) = 0 \\[1em] \Rightarrow (10x - 2)(x - 5) = 0 \\[1em] \Rightarrow 10x - 2 = 0 \text{ or } x - 5 = 0 \\[1em] \Rightarrow 10x = 2 \text{ or } x = 5 \\[1em] \Rightarrow x = \dfrac{2}{10} \text{ or } x = 5 \\[1em] \Rightarrow x = \dfrac{1}{5} \text{ or } x = 5.$

Hence, Option 1 is the correct option.

Two integers differ by 2 and sum of their squares is 52. The integers are :

1. 4 and 6

2. 4 or 6

3. -4 or 6

4. -4 and -6 or 6 and 4

Answer

Let two integers be x and x - 2.

Give,

Sum of squares = 52

⇒ x² + (x - 2)² = 52

⇒ x² + x² + 4 - 4x = 52

⇒ 2x² - 4x + 4 - 52 = 0

⇒ 2x² - 4x - 48 = 0

⇒ 2(x² - 2x - 24) = 0

⇒ x² - 2x - 24 = 0

⇒ x² - 6x + 4x - 24 = 0

⇒ x(x - 6) + 4(x - 6) = 0

⇒ (x + 4)(x - 6) = 0

⇒ x + 4 = 0 or x - 6 = 0

⇒ x = -4 or x = 6.

If x = -4,

x - 2 = -4 - 2 = -6.

If x = 6,

x - 2 = 6 - 2 = 4.

Numbers = -4 and -6 or 6 and 4.

Hence, Option 4 is the correct option.

Divide 15 into two parts such that sum of reciprocals is $\dfrac{3}{10}.$

Answer

Let numbers be x and (15 - x).

According to the question,

$\Rightarrow \dfrac{1}{x} + \dfrac{1}{15 - x} = \dfrac{3}{10} \\[1em] \Rightarrow \dfrac{15 - x + x}{x(15 - x)} = \dfrac{3}{10} \\[1em] \Rightarrow \dfrac{15}{x(15 - x)} = \dfrac{3}{10} \\[1em] \Rightarrow 150 = 3x(15 - x) \\[1em] \Rightarrow 150 = 45x - 3x^2 \\[1em] \Rightarrow 3x^2 - 45x + 150 = 0 \\[1em] \Rightarrow 3(x^2 - 15x + 50) = 0 \\[1em] \Rightarrow x^2 - 10x - 5x + 50 = 0 \\[1em] \Rightarrow x(x - 10) - 5(x - 10) = 0 \\[1em] \Rightarrow (x - 5)(x - 10) = 0 \\[1em] \Rightarrow x - 5 = 0 \text{ or } x - 10 = 0 \\[1em] \Rightarrow x = 5 \text{ or } x = 10.$

Hence, numbers = 5, 10.

The sum of the squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number, find the numbers.

Answer

Let larger number be x and smaller number be y,

According to first part,

x² + y² = 208 ........(i)

x² = 18y ........(ii)

Substituting value of x² from (ii) in (i) we get,

⇒ 18y + y² = 208

⇒ y² + 18y - 208 = 0

⇒ y² + 26y - 8y - 208 = 0

⇒ y(y + 26) - 8(y + 26) = 0

⇒ (y - 8)(y + 26) = 0

⇒ y - 8 = 0 or y + 26 = 0

⇒ y = 8 or y = -26.

Since, numbers are positive integers,

∴ y ≠ -26.

Substituting value of y = 8 in (ii),

⇒ x² = 18(8) = 144

⇒ x = $\sqrt{144} = \pm 12$.

Since, numbers are positive integers,

∴ x ≠ -12.

Hence, numbers are 12 and 8.

Find two consecutive positive odd numbers, the sum of whose squares is 74.

Answer

Let two consecutive positive odd numbers be x and (x + 2).

⇒ (x)² + (x + 2)² = 74

⇒ x² + x² + 4 + 4x = 74

⇒ 2x² + 4x + 4 - 74 = 0

⇒ 2x² + 4x - 70 = 0

⇒ 2(x² + 2x - 35) = 0

⇒ x² + 2x - 35 = 0

⇒ x² + 7x - 5x - 35 = 0

⇒ x(x + 7) - 5(x + 7) = 0

⇒ (x + 7)(x - 5) = 0

⇒ (x + 7) = 0 or (x - 5) = 0

⇒ x = -7 or x = 5.

Since, numbers are positive and even,

∴ x ≠ -7.

∴ x = 5 and (x + 2) = 7.

Hence, numbers are 5, 7.

Divide 20 into two parts such that three times the square of one part exceeds the other part by 10.

Answer

Let two parts be x and (20 - x).

According to question,

3x² - (20 - x) = 10

3x² + x - 20 = 10

3x² + x - 30 = 0

3x² + 10x - 9x - 30 = 0

x(3x + 10) - 3(3x + 10) = 0

(x - 3)(3x + 10) = 0

x - 3 = 0 or (3x + 10) = 0

x = 3 or x = $-\dfrac{10}{3}$.

20 - x = 20 - 3 = 17.

Hence, numbers are 3 and 17.

Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60.

Assume the middle number to be x and form a quadratic equation satisfying the above statement. Hence; find the three numbers.

Answer

Let three consecutive numbers be (x - 1), x and (x + 1).

According to question,

⇒ x² - [(x + 1)² - (x - 1)²] = 60

⇒ x² - [x² + 1 + 2x - (x² + 1 - 2x)] = 60

⇒ x² - [x² + 1 + 2x - x² - 1 + 2x] = 60

⇒ x² - 4x = 60

⇒ x² - 4x - 60 = 0

⇒ x² - 10x + 6x - 60 = 0

⇒ x(x - 10) + 6(x + 10) = 0

⇒ (x + 6)(x - 10) = 0

⇒ x + 6 = 0 or x - 10 = 0

⇒ x = -6 or x = 10.

Since, numbers are natural numbers,

∴ x = 10.

∴ x - 1 = 9 and x + 1 = 11.

Hence, the numbers are 9, 10, 11 and quadratic equation = x² - 4x - 60 = 0.

Out of three consecutive positive integers, the middle number is p. If three times the square of the largest is greater than the sum of the squares of the other two numbers by 67; calculate the value of p.

Answer

Let the numbers be (p - 1), p and (p + 1).

According to question,

⇒ 3(p + 1)² = (p - 1)² + p² + 67

⇒ 3(p² + 1 + 2p) = (p² + 1 - 2p) + p² + 67

⇒ 3p² + 3 + 6p = 2p² - 2p + 68

⇒ 3p² - 2p² + 6p + 2p + 3 - 68 = 0

⇒ p² + 8p - 65 = 0

⇒ p² + 13p - 5p - 65 = 0

⇒ p(p + 13) - 5(p + 13) = 0

⇒ (p - 5)(p + 13) = 0

⇒ p - 5 = 0 or p + 13 = 0

⇒ p = 5 or p = -13

Since, numbers are natural numbers,

∴ p ≠ -13.

∴ p - 1 = 4 and p + 1 = 6.

Hence, p = 5.

A positive number is divided into two parts such that the sum of the squares of the two parts is 20. The square of the larger part is 8 times the smaller part. Taking x as the smaller part of the two parts, find the number.

Answer

Let smaller part be x.

According to second part of question,

Larger part = $\sqrt{8x}$

According to first part of question,

x² + $(\sqrt{8x})^2$ = 20

x² + 8x = 20

x² + 8x - 20 = 0

x² + 10x - 2x - 20 = 0

x(x + 10) - 2(x + 10) = 0

(x - 2)(x + 10) = 0

x - 2 = 0 or x + 10 = 0

x = 2 or x = -10.

Since number is positive,

∴ x ≠ -10

Larger part = $\sqrt{8x} = \sqrt{8(2)} = \sqrt{16} = 4.$

Number = Smaller part + Larger part = 2 + 4 = 6.

Hence, number = 6.

The difference between two natural numbers is 5 and the difference of their reciprocals is $\dfrac{1}{10}$. Find the numbers.

Answer

It is given that the difference between two natural numbers = 5.

Let one number be x. So, the other number = x + 5

And, the difference of their reciprocals is $\dfrac{1}{10}$.

$\Rightarrow \dfrac{1}{x} - \dfrac{1}{x + 5} = \dfrac{1}{10}\\[1em] \Rightarrow \dfrac{x + 5}{x(x + 5)} - \dfrac{x}{x(x + 5)} = \dfrac{1}{10}\\[1em] \Rightarrow \dfrac{x + 5 - x}{x(x + 5)} = \dfrac{1}{10}\\[1em] \Rightarrow \dfrac{5}{x(x + 5)} = \dfrac{1}{10}\\[1em] \Rightarrow 5 \times 10 = x(x + 5)\\[1em] \Rightarrow 50 = x^2 + 5x\\[1em] \Rightarrow x^2 + 5x - 50 = 0\\[1em] \Rightarrow x^2 + 10x - 5x - 50 = 0\\[1em] \Rightarrow x(x + 10) - 5(x + 10) = 0\\[1em] \Rightarrow (x + 10)(x - 5) = 0\\[1em] \Rightarrow (x + 10) = 0 \text{ or }(x - 5) = 0\\[1em] \Rightarrow x = -10 \text{ or }x = 5$

It is given that numbers are natural numbers. So, number cannot be -10.

∴ x = 5

Other number = 5 + 5 = 10

Hence, the two numbers are 5 and 10.

The sum of the squares of two consecutive odd natural numbers is 394. Find the numbers.

Answer

Let the two consecutive odd natural numbers be x and x + 2.

It is given that the sum of the squares of the numbers = 394.

⇒ x² + (x + 2)² = 394

⇒ x² + x² + 2² + 4x = 394

⇒ 2x² + 4 + 4x - 394 = 0

⇒ 2x² + 4x - 390 = 0

⇒ x² + 2x - 195 = 0

⇒ x² + 15x - 13x - 195 = 0

⇒ x(x + 15) - 13(x + 15) = 0

⇒ (x + 15)(x - 13) = 0

⇒ (x + 15) = 0 or (x - 13) = 0

⇒ x = -15 or x = 13

As the number is natural number, x cannot be equal to -15. So, x = 13.

Other odd natural number = 13 + 2 = 15

Hence, the natural numbers are 13 and 15.

The sum of the squares of two consecutive multiplies of 7 is 637.

Taking the bigger number x a positive number, find the smaller of these two angles.

Answer

Let the multiplies of 7 be 7x and 7(x + 1).

It is given that the sum of the squares of two consecutive multiplies of 7 is 637.

⇒ (7x)² + [7(x + 1)]² = 637

⇒ 49x² + [7x + 7]² = 637

⇒ 49x² + 49x² + 7² + 98x - 637 = 0

⇒ 98x² + 49 + 98x - 637 = 0

⇒ 98x² + 98x - 588 = 0

⇒ x² + x - 6 = 0

⇒ x² + 3x - 2x - 6 = 0

⇒ x(x + 3) - 2(x + 3) = 0

⇒ (x + 3)(x - 2) = 0

⇒ (x + 3) = 0 or (x - 2) = 0

⇒ x = -3 or x = 2

It is given that x is bigger positive number.

So, the multiplies of 7 is 7 x 2 = 14 and 7(2 + 1) = 7 x 3 = 21

Hence, the smaller angle is 14.

Two positive numbers difference by 5. Three times the square of the larger number exceeds twice the square of smaller number by 334, find the larger of these two numbers.

Answer

It is given that difference between two positive numbers = 5.

Let the one number be x and other number be 5 + x.

Three times the square of the larger number exceeds twice the square of smaller number by 334.

⇒ 3 $\times$ (5 + x)² - 2 $\times$ x² = 334

⇒ 3 $\times$ (25 + x² + 10x) - 2 $\times$ x² = 334

⇒ 75 + 3x² + 30x - 2x² - 334 = 0

⇒ x² + 30x - 259 = 0

⇒ x² + 37x - 7x - 259 = 0

⇒ x(x + 37) - 7(x + 37) = 0

⇒ (x + 37)(x - 7) = 0

⇒ (x + 37) = 0 or (x - 7) = 0

⇒ x = -37 or x = 7

Larger number = 5 + x = 5 + 7 = 12

Hence, the larger number = 12.

The sum of the numerator and the denominator is 8 and their product is 15. Then the fraction is:

1. $\dfrac{5}{3}$ and $\dfrac{3}{5}$

2. $\dfrac{5}{3}$ or $\dfrac{3}{5}$

3. 3 and 5

4. 3 or 5

Answer

$\dfrac{5}{3}$ or $\dfrac{3}{5}$

Reason

It is given that the sum of the numerator and the denominator is 8.

Let the numerator of the fraction be x. So, denominator of the fraction = 8 - x

And, the product of numerator and denominator is 15.

⇒ x(8 - x) = 15

⇒ 8x - x² = 15

⇒ 8x - x² - 15 = 0

⇒ x² - 8x + 15 = 0

⇒ x² - 5x - 3x + 15 = 0

⇒ x(x - 5) - 3(x - 5) = 0

⇒ (x - 5)(x - 3) = 0

⇒ (x - 5) = 0 or (x - 3) = 0

⇒ x = 5 or x = 3

When x = 5, denominator = 8 - 5 = 3

When x = 3, denominator = 8 - 3 = 5

So, the fraction = $\dfrac{5}{3} \text{ or } \dfrac{3}{5}$.

Hence, option 2 is the correct option.

The sum of the digits of a two digit number is 9 and the product of the digits is 20. If the unit digit is greater than the tens digit. The number is

1. 45

2. 54

3. none of these

Answer

54

Reason

Let tens digit be x and units digit be y.

Given,

x + y = 9
xy = 20

From x + y = 9, we have y = 9 - x

Substituting in xy = 20, we get,

⇒ x(9 - x) = 20

⇒ 9x - x² = 20

⇒ 9x - x² - 20 = 0

⇒ x² - 9x + 20 = 0

⇒ x² - 4x - 5x + 20 = 0

⇒ x(x - 4) - 5(x - 4) = 0

⇒ (x - 4)(x - 5) = 0

⇒ (x - 4) = 0 or (x - 5) = 0

⇒ x = 4 or x = 5

When x = 4, y = 9 - 4 = 5

When x = 5, y = 9 - 5 = 4

The problem states "the unit digit is greater than the tens digit", so we need y > x.

∴ x = 4 and y = 5

∴ The number is 45

Hence, option 1 is the correct option.

Two whole numbers are in ratio 3:2. If the sum of their square is 52, the numbers are:

1. 9 and 6

2. 6 and 4

3. 9 and 4

4. none of these

Answer

6 and 4

Reason

It is given that two whole numbers are in ratio 3:2.

Let the numbers be 3x and 2x.

The sum of their square = 52.

⇒ (3x)² + (2x)² = 52

⇒ 9x² + 4x² = 52

⇒ 13x² = 52

⇒ x² = $\dfrac{52}{13}$

⇒ x² = 4

⇒ x = $\sqrt{4}$

⇒ x = $\pm$ 2

So, the numbers = 3x = 3 x 2 or 3 x (-2) = 6 or -6

2x = 2 x 2 or 2 x (-2) = 4 or -4

Since, the given numbers are whole numbers. So, the numbers cannot be -6 and -4.

Hence, option 2 is the correct option.

A two digit number is 5 times the sum of its digits. The number is:

1. 63

2. 36

3. 45

4. 54

Answer

45

Reason

Let the two digit number be 10x + y.

It is given that two digit number is 5 times the sum of its digits

⇒ 10x + y = 5(x + y)

⇒ 10x + y = 5x + 5y

⇒ 10x - 5x = 5y - y

⇒ 5x = 4y

⇒ y = $\dfrac{5}{4}$x

As x and y are digits, so

x ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9}

and

y ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Since y must be a single digit integer, x must be a multiple of 4. The only possible values for x from the above set are x = 4 and x = 8.

For x = 4, y = $\dfrac{5}{4} \times$ 4 = 5

For x = 8, y = $\dfrac{5}{4} \times$ 8 = 10 which is not a valid digit.

∴ Valid digits are x = 4 and y = 5.

∴ The number = 10 × 4 + 5 = 45

Hence, option 3 is the correct option.

Three positive numbers are in ratio 4 : 3 : 2. If the difference between square of the largest and the smallest number is 48, the numbers are;

1. 48, 36 and 24

2. 24, 18 and 12

3. 8, 6 and 2

4. 8, 6 and 4

Answer

8, 6 and 4

Reason

It is given that three positive numbers are in ratio 4 : 3 : 2.

Let the numbers be 4x, 3x and 2x.

The difference between square of the largest and the smallest number = 48.

⇒ (4x)² - (2x)² = 48

⇒ 16x² - 4x² = 48

⇒ 12x² = 48

⇒ x² = $\dfrac{48}{12}$

⇒ x² = 4

⇒ x = $\sqrt{4}$

⇒ x = $\pm$ 2

So, the numbers are 4x = 4 x 2 or 4 x (-2) = 8 or -8

3x = 3 x 2 or 3 x (-2) = 6 or -6

2x = 2 x 2 or 2 x (-2) = 4 or -4

The numbers are positive numbers. So, the numbers cannot be -8, -6 and -4.

∴ The numbers are 8, 6 and 4

Hence, option 4 is the correct option.

The numerator of a fraction is 3 less than its denominator. If one is added to the denominator, the fraction is decreased by $\dfrac{1}{15}$. Find the fraction.

Answer

Let the fraction be $\dfrac{a}{b}$.

It is given that the numerator of a fraction is 3 less than its denominator.

⇒ a = b - 3

And, one is added to the denominator, the fraction is decreased by $\dfrac{1}{15}$.

$\Rightarrow \dfrac{a}{b + 1} = \dfrac{a}{b} - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{b - 3}{b + 1} = \dfrac{b - 3}{b} - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{b - 3}{b + 1} - \dfrac{b - 3}{b} = - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{b(b - 3) - (b + 1)(b - 3)}{b(b + 1)} = - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{(b^2 - 3b) - (b^2 - 3b + b - 3)}{b(b + 1)} = - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{b^2 - 3b - b^2 + 3b - b + 3}{b(b + 1)} = - \dfrac{1}{15}\\[1em] \Rightarrow \dfrac{ - b + 3}{b^2 + b} = - \dfrac{1}{15}\\[1em] \Rightarrow 15(-b + 3) = - 1(b^2 + b)\\[1em] \Rightarrow - 15b + 45 = - b^2 - b\\[1em] \Rightarrow - 15b + 45 + b^2 + b = 0\\[1em] \Rightarrow b^2 - 14b + 45 = 0\\[1em] \Rightarrow b^2 - 9b - 5b + 45 = 0\\[1em] \Rightarrow b(b - 9) - 5(b - 9) = 0\\[1em] \Rightarrow (b - 9)(b - 5) = 0\\[1em] \Rightarrow (b - 9) = 0 \text{ or }(b - 5) = 0\\[1em] \Rightarrow b = 9 \text{ or }b = 5\\[1em]$

If b = 9, then a = 9 - 3 = 6

And, if b = 5, then a = 5 - 3 = 2

So, the fraction = $\dfrac{6}{9} = \dfrac{2}{3} \text{ or }\dfrac{2}{5}$

Hence, the fraction = $\dfrac{2}{3} \text{ or } \dfrac{2}{5}$.

The denominator of a fraction is 3 more than its numerator. The sum of the fraction and its reciprocal is $2\dfrac{9}{10}$. Find the fraction.

Answer

Let the fraction be $\dfrac{a}{b}$.

It is given that the denominator of a fraction is 3 more than its numerator.

⇒ b = a + 3

And, the sum of the fraction and its reciprocal is $2\dfrac{9}{10}$.

$\Rightarrow \dfrac{a}{b} + \dfrac{b}{a} = 2\dfrac{9}{10}\\[1em] \Rightarrow \dfrac{a}{a + 3} + \dfrac{a + 3}{a} = \dfrac{29}{10}\\[1em] \Rightarrow \dfrac{(a \times a) + [(a + 3)(a + 3)] }{(a + 3)a} = \dfrac{29}{10}\\[1em] \Rightarrow \dfrac{a^2 + (a + 3)^2}{(a + 3)a} = \dfrac{29}{10}\\[1em] \Rightarrow \dfrac{a^2 + (9 + 6a + a^2)}{(a + 3)a} = \dfrac{29}{10}\\[1em] \Rightarrow \dfrac{a^2 + 9 + 6a + a^2}{3a + a^2} = \dfrac{29}{10}\\[1em] \Rightarrow 10(a^2 + 9 + 6a + a^2) = 29(3a + a^2)\\[1em] \Rightarrow 10(2a^2 + 9 + 6a) = 29(3a + a^2)\\[1em] \Rightarrow 20a^2 + 90 + 60a = 87a + 29a^2\\[1em] \Rightarrow 20a^2 + 90 + 60a - 87a - 29a^2 = 0\\[1em] \Rightarrow -9a^2 - 27a + 90 = 0\\[1em] \Rightarrow a^2 + 3a - 10 = 0\\[1em] \Rightarrow a^2 + 5a - 2a - 10 = 0\\[1em] \Rightarrow a(a + 5) - 2(a + 5) = 0\\[1em] \Rightarrow (a + 5)(a - 2) = 0\\[1em] \Rightarrow (a + 5) = 0 \text{ or }(a - 2) = 0\\[1em] \Rightarrow a = -5 \text{ or } a = 2\\[1em]$

If a = -5, then b = 3 + (-5) = -2

And, if a = 2, then b = 3 + 2 = 5

So, the fraction = $\dfrac{-5}{-2} = \dfrac{5}{2} \text{ or }\dfrac{2}{5}$

Since, denominator is 3 more than the numerator,

∴ The fraction is $\dfrac{2}{5}$

Hence, the fraction = $\dfrac{2}{5}$.

The product of the digits of a two digit number is 24. If it's unit's digits exceeds twice it's ten's digit by 2; find the number.

Answer

Let unit's digit be x and ten's digit be y.

According to question,

⇒ xy = 24 ........(i)

⇒ x = 2y + 2 ........(ii)

Substituting value of x from (ii) in (i) we get,

⇒ (2y + 2)y = 24

⇒ 2y² + 2y = 24

⇒ y² + y = 12

⇒ y² + y - 12 = 0

⇒ y² + 4y - 3y - 12 = 0

⇒ y(y + 4) - 3(y + 4) = 0

⇒ (y - 3)(y + 4) = 0

⇒ y - 3 = 0 or y + 4 = 0

⇒ y = 3 or y = -4.

Since digit at ten's place cannot be negative

∴ y ≠ -4.

⇒ x = 2y + 2 = 2(3) + 2 = 8

Number = 10(y) + x = 10(3) + 8 = 38.

Hence, number = 38.

A two-digit number is such that the product of its digit is 18. When 63 is subtracted from the number, the digits are reserved. Find the number.

Answer

Let tens digit be x and units digit be y.

Given,

$xy = 18 \\[1em] \Rightarrow y = \dfrac{18}{x}$

The number = 10x + y = $10 \times x + \dfrac{18}{x} = \dfrac{10x^2 + 18}{x}$

Reversed number = 10y + x = $10 \times \dfrac{18}{x} + x = \dfrac{180 + x^2}{x}$

Given,
if 63 is subtracted from the number, the digits are reserved.

$\Rightarrow \dfrac{10x^2 + 18}{x} - 63 = \dfrac{180 + x^2}{x}\\[1em] \Rightarrow \dfrac{10x^2 + 18 - 63x}{x} = \dfrac{180 + x^2}{x}\\[1em] \Rightarrow 10x^2 + 18 - 63x = 180 + x^2\\[1em] \Rightarrow 10x^2 + 18 - 63x - 180 - x^2 = 0\\[1em] \Rightarrow 9x^2 - 63x - 162 = 0\\[1em] \Rightarrow x^2 - 7x - 18 = 0\\[1em] \Rightarrow x^2 - 9x + 2x - 18 = 0\\[1em] \Rightarrow x(x - 9) + 2(x - 9) = 0\\[1em] \Rightarrow (x - 9)(x + 2) = 0\\[1em] \Rightarrow (x - 9) = 0 \text{ or } (x + 2) = 0\\[1em] \Rightarrow x = 9 \text{ or } x = - 2$

As the digit of a number cannot be negative. So x = 9.

y = $\dfrac{18}{x} = \dfrac{18}{9}$ = 2

The number = 10x + y = 10 $\times$ 9 + 2 = 90 + 2 = 92

Hence, the number = 92.

The ratio between two positive numbers is $\dfrac{1}{5}:\dfrac{1}{7}$. If the sum of the squares of the numbers is 666, find the numbers.

Answer

It is given that the ratio between two positive numbers is $\dfrac{1}{5}:\dfrac{1}{7}$.

Let the two numbers be $\dfrac{1}{5}x$ and $\dfrac{1}{7}x$.

The sum of the squares of the numbers = 666.

$\Rightarrow \Big(\dfrac{1}{5}x\Big)^2 + \Big(\dfrac{1}{7}x\Big)^2 = 666\\[1em] \Rightarrow \dfrac{1}{25}x^2 + \dfrac{1}{49}x^2 = 666\\[1em] \Rightarrow \dfrac{1 \times 49}{25 \times 49}x^2 + \dfrac{1 \times 25}{49 \times 25}x^2 = 666\\[1em] \Rightarrow \dfrac{49}{1,225}x^2 + \dfrac{25}{1,225}x^2 = 666\\[1em] \Rightarrow \dfrac{74}{1,225}x^2 = 666\\[1em] \Rightarrow x^2 = \dfrac{666 \times 1,225}{74}\\[1em] \Rightarrow x^2 = \dfrac{8,15,850}{74}\\[1em] \Rightarrow x^2 = 11,025\\[1em] \Rightarrow x = \sqrt{11,025}\\[1em] \Rightarrow x = 105$

So, the numbers = $\dfrac{1}{5}x = \dfrac{1}{5} \times 105$ = 21 and $\dfrac{1}{7}x = \dfrac{1}{7} \times 105$ = 15

Hence, the two numbers = 21 and 15.

The ratio between three positive numbers is $\dfrac{1}{4} : \dfrac{1}{3} : \dfrac{1}{2}$. When the square of the middle number is subtracted from the sum of the squares of the other, the result is 725. Find the numbers.

Answer

It is given that the ratio between three positive numbers = $\dfrac{1}{4} : \dfrac{1}{3} : \dfrac{1}{2}$

Let the three number be $\dfrac{1}{4}x, \dfrac{1}{3}x \text{ and } \dfrac{1}{2}x$.

If the square of the middle number is subtracted from the sum of the squares of the other, the result is 725.

$\Rightarrow \Big[\Big(\dfrac{1}{4}x\Big)^2 + \Big(\dfrac{1}{2}x\Big)^2\Big] - \Big(\dfrac{1}{3}x\Big)^2 = 725\\[1em] \Rightarrow \Big[\dfrac{1}{16}x^2 + \dfrac{1}{4}x^2\Big] - \dfrac{1}{9}x^2 = 725\\[1em] \Rightarrow \Big[\dfrac{1}{16}x^2 + \dfrac{1 \times 4}{4 \times 4}x^2\Big] - \dfrac{1}{9}x^2 = 725\\[1em] \Rightarrow \Big[\dfrac{1}{16}x^2 + \dfrac{4}{16}x^2\Big] - \dfrac{1}{9}x^2 = 725\\[1em] \Rightarrow \dfrac{5}{16}x^2 - \dfrac{1}{9}x^2 = 725\\[1em] \Rightarrow \dfrac{5 \times 9}{16 \times 9}x^2 - \dfrac{1 \times 16}{9 \times 16}x^2 = 725\\[1em] \Rightarrow \dfrac{45}{144}x^2 - \dfrac{16}{144}x^2 = 725\\[1em] \Rightarrow \dfrac{29}{144}x^2 = 725\\[1em] \Rightarrow x^2 = \dfrac{725 \times 144}{29}\\[1em] \Rightarrow x^2 = \dfrac{104,400}{29}\\[1em] \Rightarrow x^2 = 3,600\\[1em] \Rightarrow x = \sqrt{3,600}\\[1em] \Rightarrow x = 60$

So, the numbers = $\dfrac{1}{4}x = \dfrac{1}{4} \times 60 = 15, \dfrac{1}{3}x = \dfrac{1}{3} \times 60 = 20 \text{ and } \dfrac{1}{2}x = \dfrac{1}{2} \times 60 = 30$

Hence, the number = 15, 20 and 30.

The numerator of a fraction is 3 less than its denominator. If 2 is added to both the numerator and denominator, the sum of the new fraction and the original fraction is $1\dfrac{9}{20}$. Find the new fraction.

Answer

Let the fraction be $\dfrac{a}{b}$.

It is given that the numerator of a fraction is 3 less than its denominator.

⇒ a = b - 3

And, If 2 is added to both the numerator and denominator, the sum of the new fraction and the original fraction is $1\dfrac{9}{20}$

$\Rightarrow \dfrac{a}{b} + \dfrac{a + 2}{b + 2} = 1\dfrac{9}{20}\\[1em] \Rightarrow \dfrac{b - 3}{b} + \dfrac{(b - 3) + 2}{b + 2} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{b - 3}{b} + \dfrac{b - 1}{b + 2} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{(b - 3) \times (b + 2)}{b \times (b + 2)} + \dfrac{(b - 1) \times b}{(b + 2) \times b} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{b^2 - 3b + 2b - 6}{b^2 + 2b} + \dfrac{b^2 - b}{b^2 + 2b} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{(b^2 - 3b + 2b - 6) + (b^2 - b)}{b^2 + 2b} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{b^2 - b - 6 + b^2 - b}{b^2 + 2b} = \dfrac{29}{20}\\[1em] \Rightarrow \dfrac{2b^2 - 2b - 6}{b^2 + 2b} = \dfrac{29}{20}\\[1em] \Rightarrow 20(2b^2 - 2b - 6) = 29(b^2 + 2b)\\[1em] \Rightarrow 40b^2 - 40b - 120 = 29b^2 + 58b\\[1em] \Rightarrow 40b^2 - 40b - 120 - 29b^2 - 58b = 0\\[1em] \Rightarrow 11b^2 - 98b - 120 = 0\\[1em] \Rightarrow 11b^2 - 110b + 12b - 120 = 0\\[1em] \Rightarrow 11b(b - 10) + 12(b - 10) = 0\\[1em] \Rightarrow (b - 10)(11b + 12) = 0\\[1em] \Rightarrow (b - 10) = 0 \text{ or } (11b + 12) = 0\\[1em] \Rightarrow b = 10 \text{ or } b = -\dfrac{12}{11}\\[1em]$

As b cannot be fraction. So, b = 10.

When b = 10, a = b - 3 = 10 - 3 = 7

The fraction = $\dfrac{a}{b} = \dfrac{7}{10}$

New fraction = $\dfrac{a + 2}{b + 2} = \dfrac{7 + 2}{10 + 2} = \dfrac{9}{12} = \dfrac{3}{4}$

Hence, the fraction = $\dfrac{3}{4}$.

A two digit number is 4 times the sum of its digits and twice the product of its digits. Find the number.

Answer

Let the two-digit number be 10x + y.

If the number is 4 times the sum of its digits.

⇒ 10x + y = 4(x + y)

⇒ 10x + y = 4x + 4y

⇒ 10x - 4x = 4y - y

⇒ 6x = 3y

⇒ 2x = y .......... (1)

And, the number is twice the product of its digits.

⇒ 10x + y = 2(xy)

Using equation (1), we get

⇒ 10x + 2x = 2(x $\times$ 2x)

⇒ 12x = 2(2x²)

⇒ 12x = 4x²

⇒ 12 = 4x

⇒ 3 = x

Putting the value of x in equation (1), we get

y = 2x = 2 $\times$ 3 = 6

The number = 10x + y = 10 $\times$ 3 + 6 = 30 + 6 = 36

Hence, the number = 36.

27 is divided into two parts such that the sum of their reciprocal is $\dfrac{3}{20}$. Find the ratio between the numbers (5 : 4).

Answer

Let one number be x and the other number = (27 - x).

The sum of their reciprocal = $\dfrac{3}{20}$

$\Rightarrow \dfrac{1}{x} + \dfrac{1}{27 - x} = \dfrac{3}{20}\\[1em] \Rightarrow \dfrac{27 - x}{x(27 - x)} + \dfrac{x}{x(27 - x)} = \dfrac{3}{20}\\[1em] \Rightarrow \dfrac{27 - x + x}{x(27 - x)} = \dfrac{3}{20}\\[1em] \Rightarrow \dfrac{27}{27x - x^2} = \dfrac{3}{20}\\[1em] \Rightarrow 27 \times 20 = 3 \times (27x - x^2)\\[1em] \Rightarrow 540 = 81x - 3x^2\\[1em] \Rightarrow 81x - 3x^2 - 540 = 0\\[1em] \Rightarrow x^2 - 27x + 180 = 0\\[1em] \Rightarrow x^2 - 12x - 15x + 180 = 0\\[1em] \Rightarrow x(x - 12) - 15(x - 12) = 0\\[1em] \Rightarrow (x - 12)(x - 15) = 0\\[1em] \Rightarrow (x - 12) = 0 \text{ or } (x - 15) = 0\\[1em] \Rightarrow x = 12 \text{ or } x = 15\\[1em]$

If one number = 12, other number = 27 - 12 = 15

If one number = 15, other number = 27 - 15 = 12

Ratio = 12 : 15 = 4 : 5 or 15 : 12 = 5 : 4

Hence, the ratio of two numbers = 5 : 4.

A and B together can do a piece of work in 6 days. Whereas A alone can do the same work in 9 days. Then B alone will do same work in:

1. 15 days

2. 6 days

3. 18 days

4. 54 days

Answer

18 days

Reason

Given,

A alone can do the same work in 9 days.

So, one day work of A = $\dfrac{1}{9}$

Let B alone can do the same work in y days.

So, one day work of B = $\dfrac{1}{y}$

As together they can do work in 6 days.

∴ In one day, both of them do $\dfrac{1}{6}$th part of work.

$∴ \dfrac{1}{9} + \dfrac{1}{y} = \dfrac{1}{6}\\[1em] \Rightarrow \dfrac{1 \times y}{9\times y} + \dfrac{1\times 9}{y\times 9} = \dfrac{1}{6}\\[1em] \Rightarrow \dfrac{y}{9y} + \dfrac{9}{9y} = \dfrac{1}{6}\\[1em] \Rightarrow \dfrac{y + 9}{9y} = \dfrac{1}{6}\\[1em] \Rightarrow 6(y + 9) = 9y\\[1em] \Rightarrow 6y + 54 = 9y\\[1em] \Rightarrow 9y - 6y = 54\\[1em] \Rightarrow 3y = 54\\[1em] \Rightarrow y = \dfrac{54}{3}\\[1em] \Rightarrow y = 18$

∴ B alone can complete the work in 18 days.

Hence, option 3 is the correct option.

A can do a piece of work in 5 days and B can do the same work in (x + 5) days. The total number of days taken by A and B, working together, $3\dfrac{1}{3}$. The value of x is :

1. 5

2. 10

3. 15

4. $2\dfrac{1}{2}$

Answer

A can do a piece of work in 5 days.

So, in 1 day

A will do $\dfrac{1}{5}$ th of the work.

B can do a piece of work in (x + 5) days.

So, in 1 day

B will do $\dfrac{1}{x + 5}$ of the work.

Work done by A and B in 1 day = $\dfrac{1}{5} + \dfrac{1}{x + 5}$

Days taken to complete work = $\dfrac{1}{\text{Work done by A and B in 1 day}}$

$\Rightarrow 3\dfrac{1}{3} = \dfrac{1}{\dfrac{1}{5} + \dfrac{1}{x + 5}} \\[1em] \Rightarrow \dfrac{10}{3} = \dfrac{1}{\dfrac{x + 5 + 5}{5(x + 5)}} \\[1em] \Rightarrow \dfrac{10}{3} = \dfrac{5(x + 5)}{x + 10} \\[1em] \Rightarrow \dfrac{10}{3} = \dfrac{5x + 25}{x + 10} \\[1em] \Rightarrow 10(x + 10) = 3(5x + 25) \\[1em] \Rightarrow 10x + 100 = 15x + 75 \\[1em] \Rightarrow 15x - 10x = 100 -75 \\[1em] \Rightarrow 5x = 25 \\[1em] \Rightarrow x = \dfrac{25}{5} = 5.$

Hence, Option 1 is the correct option.

An article is bought for ₹ x and is sold at the profit of x %. If its selling price is ₹ 56, the cost price is :

1. ₹ 60

2. ₹ 50

3. ₹ 40

4. ₹ 28

Answer

Given,

C.P. = ₹ x

Profit = x %

S.P. = C.P. + Profit

$\Rightarrow 56 = x + \dfrac{x}{100} \times x \\[1em] \Rightarrow 56 = x + \dfrac{x^2}{100} \\[1em] \Rightarrow \dfrac{x^2 + 100x}{100} = 56 \\[1em] \Rightarrow x^2 + 100x = 5600 \\[1em] \Rightarrow x^2 + 100x - 5600 = 0\\[1em] \Rightarrow x^2 + 140x - 40x - 5600 = 0 \\[1em] \Rightarrow x(x + 140) - 40(x + 140) = 0 \\[1em] \Rightarrow (x - 40)(x + 140) = 0 \\[1em] \Rightarrow x - 40 = 0 \text{ or }x + 140 =0 \\[1em] \Rightarrow x = 40 \text{ or } x = -140.$

Since, cost cannot be negative.

∴ x ≠ -140.

Hence, Option 3 is the correct option.

An empty tank is filled by a pipe in 2 hours, whereas an another pipe empties the full tank in 3 hours. If the tank is empty and both the pipes are opened together the tank will be filled in:

1. 5 hours

2. 1 hour

3. 6 hours

4. none of these

Answer

6 hours

Reason

Given,

An empty tank is filled by a pipe in 2 hours.

So, one hour work of the pipe = $\dfrac{1}{2}$

Another pipe empties the full tank in 3 hours.

So, one hour work of other pipe = -$\dfrac{1}{3}$

When both pipes are opened together

$= \dfrac{1}{2} + \Big(-\dfrac{1}{3}\Big)\\[1em] = \dfrac{1}{2} - \dfrac{1}{3}\\[1em] = \dfrac{1 \times 3}{2 \times 3} - \dfrac{1 \times 2}{3 \times 2}\\[1em] = \dfrac{3}{6} - \dfrac{2}{6}\\[1em] = \dfrac{1}{6}$

Total time taken to fill the tank = $\dfrac{1}{\dfrac{1}{6}}$ = 6 hours.

Hence, option 3 is the correct option.

A can do a piece of work in 'x' days and B can do the same work in (x + 16) days. If both working together can do it in 15 days; calculate 'x'.

Answer

A can do work in x days

B can do work in (x + 16) days

In one day, A completes $\dfrac{1}{x}$ part of work

In one day, B completes $\dfrac{1}{x + 16}$ part of work

Given, both can do work in 15 days,

$\therefore \dfrac{1}{x} + \dfrac{1}{x + 16} = \dfrac{1}{15} \\[1em] \dfrac{x + 16 + x}{x(x + 16)} = \dfrac{1}{15} \\[1em] \dfrac{2x + 16}{x^2 + 16x} = \dfrac{1}{15} \\[1em] 15(2x + 16) = x^2 + 16x \\[1em] 30x + 240 = x^2+ 16x \\[1em] x^2 + 16x - 30x - 240 = 0 \\[1em] x^2 - 14x - 240 = 0 \\[1em] x^2 - 24x + 10x - 240 = 0 \\[1em] x(x - 24) + 10(x - 24) = 0 \\[1em] (x + 10)(x - 24) = 0 \\[1em] x + 10 = 0 \text{ or } x - 24 = 0 \\[1em] x = -10 \text{ or } x = 24.$

Since, no. of days cannot be negative,

∴ x ≠ -10.

Hence, x = 24 days.

One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.

Answer

Let second pipe fill in x hours, and first pipe in (x - 3) hours.

In one hour second pipe will fill $\dfrac{1}{x}$ and first pipe $\dfrac{1}{x - 3}$.

Given, together pipes can fill the cistern in 6 hours 40 minutes i.e. $\dfrac{400}{60}$ hours.

Hence, in one hour they will fill $\dfrac{1}{\dfrac{400}{60}} = \dfrac{60}{400}$.

$\therefore \dfrac{1}{x} + \dfrac{1}{x - 3} = \dfrac{60}{400} \\[1em] \Rightarrow \dfrac{x - 3 + x}{x(x - 3)} = \dfrac{3}{20} \\[1em] \Rightarrow \dfrac{2x - 3}{x^2 - 3x} = \dfrac{3}{20} \\[1em] \Rightarrow 20(2x - 3) = 3(x^2 - 3x) \\[1em] \Rightarrow 40x - 60 = 3x^2 - 9x \\[1em] \Rightarrow 3x^2 - 9x - 40x - 60 = 0 \\[1em] \Rightarrow 3x^2 - 49x - 60 = 0 \\[1em] \Rightarrow 3x^2 - 45x - 4x - 60 = 0 \\[1em] \Rightarrow 3x(x - 15) - 4(x - 15) = 0 \\[1em] \Rightarrow (3x - 4)(x - 15) = 0 \\[1em] \Rightarrow 3x - 4 = 0 \text{ or } x - 15 = 0 \\[1em] \Rightarrow x = \dfrac{4}{3} \text{ or } x = 15.$

Since first pipe takes 3 hours less than second pipe,

∴ x ≠ $\dfrac{4}{3}$ as in this case time will be negative which is not possible.

∴ x = 15, x - 3 = 12.

Hence, pipes will take 12 hours and 15 hours to fill cistern separately.

A trader bought an article for ₹ x and sold it for ₹ 52, thereby making a profit of (x - 10) percent on his outlay. Calculate the cost price.

Answer

C.P. = ₹ x

S.P. = ₹ 52

Profit = S.P. - C.P. = ₹(52 - x)

Profit % = $\dfrac{\text{Profit}}{\text{C.P.}} \times 100$

Substituting value in above equation we get,

$\Rightarrow x - 10 = \dfrac{52 - x}{x} \times 100 \\[1em] \Rightarrow x(x - 10) = 100(52 - x) \\[1em] \Rightarrow x^2 - 10x = 5200 - 100x \\[1em] \Rightarrow x^2 - 10x + 100x - 5200 = 0 \\[1em] \Rightarrow x^2 + 90x - 5200 = 0 \\[1em] \Rightarrow x^2 + 130x - 40x - 5200 = 0 \\[1em] \Rightarrow x(x + 130) - 40(x + 130) = 0 \\[1em] \Rightarrow (x - 40)(x + 130) = 0 \\[1em] \Rightarrow (x - 40) = 0 \text{ or } (x + 130) = 0 \\[1em] \Rightarrow x = 40 \text{ or } x = -130.$

Since, cost cannot be negative

∴ x ≠ -130.

Hence, C.P. = ₹ 40

The C.P. of an article is ₹ x which is sold for ₹ 27 at a loss of (x - 5) percent; find the value of x.

Answer

Given,

C.P. = ₹ x

S.P. = ₹ 27

Loss = (x - 5) %

Loss = C.P. - S.P.

= ₹ (x - 27)

As we know that Loss % = $\dfrac{\text{Loss}}{\text{C.P.}} \times 100$

Substituting the values, we get

$\Rightarrow (x - 5) = \dfrac{(x - 27)}{x} \times 100 \\[1em] \Rightarrow x(x - 5) = (x - 27) \times 100 \\[1em] \Rightarrow x^2 - 5x = 100x - 2700 \\[1em] \Rightarrow x^2 - 5x - 100x + 2700 = 0\\[1em] \Rightarrow x^2 - 105x + 2700 = 0\\[1em] \Rightarrow x^2 - 45x - 60x + 2700 = 0\\[1em] \Rightarrow x(x - 45) - 60(x - 45) = 0\\[1em] \Rightarrow (x - 45)(x - 60) = 0\\[1em] \Rightarrow (x - 45) = 0 \text{ or } (x - 60) = 0\\[1em] \Rightarrow x = 45 \text{ or } x = 60\\[1em]$

Hence, the value of C.P. = ₹ 45 or ₹ 60.

The C.P. of an article is ₹ x which is sold for ₹ 152 at a profit of (x + 10)%. Find the value of x.

Answer

Given,

C.P. = ₹ x

S.P. = ₹ 152

Profit = (x + 10) %

Profit = S.P. - C.P.

= ₹ (152 - x)

As we know that Profit % = $\dfrac{\text{Profit}}{\text{C.P.}} \times 100$

Substituting the values, we get

$\Rightarrow (x + 10) = \dfrac{(152 - x)}{x} \times 100 \\[1em] \Rightarrow x(x + 10) = (152 - x) \times 100 \\[1em] \Rightarrow x^2 + 10x = 15200 - 100x \\[1em] \Rightarrow x^2 + 10x - 15200 + 100x = 0\\[1em] \Rightarrow x^2 + 110x - 15200 = 0\\[1em] \Rightarrow x^2 + 190x - 80x - 15200 = 0\\[1em] \Rightarrow x(x + 190) - 80(x + 190) = 0\\[1em] \Rightarrow (x + 190)(x - 80) = 0\\[1em] \Rightarrow (x + 190) = 0 \text{ or } (x - 80) = 0\\[1em] \Rightarrow x = -190 \text{ or } x = 80\\[1em]$

The cost price of the article cannot be negative.

Hence, the value of C.P. = ₹ 80.

Two pipes running together can fill an empty cistern in $4\dfrac{20}{21}$ minutes. If one pipe takes 5 minutes more than the other pipe to fill the empty cistern. Find the time in which each pipe would fill the cistern.

Answer

Let the time taken by each pipe be x minutes and y minutes.

It is given that one pipe takes 5 minutes more than the other pipe to fill the empty cistern.

⇒ x = y + 5

So, one minute work of the pipe = $\dfrac{1}{x} = \dfrac{1}{y + 5}$

And, one minute work of the other pipe = $\dfrac{1}{y}$

Both pipes running together can fill the empty cistern in $4\dfrac{20}{21} = \dfrac{104}{21}$ minutes.

$\Rightarrow \dfrac{1}{x} + \dfrac{1}{y} = \dfrac{21}{104}\\[1em] \Rightarrow \dfrac{1}{y + 5} + \dfrac{1}{y} = \dfrac{21}{104}\\[1em] \Rightarrow \dfrac{1 \times y}{y(y + 5)} + \dfrac{1 \times (y + 5)}{y(y + 5)} = \dfrac{21}{104}\\[1em] \Rightarrow \dfrac{y}{y(y + 5)} + \dfrac{y + 5}{y(y + 5)} = \dfrac{21}{104}\\[1em] \Rightarrow \dfrac{y + y + 5}{y(y + 5)} = \dfrac{21}{104}\\[1em] \Rightarrow \dfrac{2y + 5}{y^2 + 5y} = \dfrac{21}{104}\\[1em] \Rightarrow 104(2y + 5) = 21(y^2 + 5y)\\[1em] \Rightarrow 208y + 520 = 21y^2 + 105y\\[1em] \Rightarrow 21y^2 + 105y - 208y - 520 = 0\\[1em] \Rightarrow 21y^2 - 103y - 520 = 0\\[1em] \Rightarrow 21y^2 + 65y - 168y - 105 = 0\\[1em] \Rightarrow y(21y + 65) - 8(21y + 65) = 0\\[1em] \Rightarrow (21y + 65)(y - 8) = 0\\[1em] \Rightarrow (21y + 65) = 0 \text{ or }(y - 8) = 0\\[1em] \Rightarrow y = -\dfrac{65}{21} \text{ or }y = 8\\[1em]$

As minutes cannot be negative.

So, one pipe takes 8 minutes and the other pipe takes 8 + 5 = 13 minutes.

Hence, the time taken by pipes = 8 minutes and 13 minutes.

In order to fill an empty swimming pool completely, a pipe of larger diameter alone takes 10 hour less than the time taken by the pipe of the smaller diameter alone. If the pipe of the larger diameter is used for 4 hours and the pipe of the smaller diameter is used for 9 hours, half of the pool is filled. In how many hours will the pipe of the larger diameter alone fill the pool.

Answer

Let the time taken by the larger diameter pipe to fill the pool alone be L hours and the time taken by the smaller diameter pipe to fill the pool alone be S hours.

From the problem, we know that the larger diameter pipe takes 10 hours less than the smaller diameter pipe. Hence, we can write the relationship as:

⇒ L = S - 10

The rate of the larger pipe is $\dfrac{1}{\text{L}}$ of the pool per hour.

The rate of the smaller pipe is $\dfrac{1}{\text{S}}$ of the pool per hour.

It is given that when the larger pipe is used for 4 hours and the smaller pipe is used for 9 hours, half of the pool is filled. So, the total work done in this scenario can be expressed as:

⇒ $4 \times \dfrac{1}{\text{L}} + 9 \times \dfrac{1}{\text{S}} = \dfrac{1}{2}$

Substituting the value of L = S - 10, we get

$\Rightarrow 4 \times \dfrac{1}{S - 10} + 9 \times \dfrac{1}{\text{S}} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{4}{S - 10} + \dfrac{9}{\text{S}} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{4S}{S(S - 10)} + \dfrac{9(S - 10)}{S(S - 10)} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{4S}{S(S - 10)} + \dfrac{9S - 90}{S(S - 10)} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{4S + 9S - 90}{S(S - 10)} = \dfrac{1}{2}\\[1em] \Rightarrow \dfrac{13S - 90}{S^2 - 10S} = \dfrac{1}{2}\\[1em] \Rightarrow 2(13S - 90) = S^2 - 10S\\[1em] \Rightarrow 26S - 180 = S^2 - 10S\\[1em] \Rightarrow S^2 - 10S - 26S + 180 = 0\\[1em] \Rightarrow S^2 - 36S + 180 = 0\\[1em] \Rightarrow S^2 - 30S - 6S + 180 = 0\\[1em] \Rightarrow S(S - 30) - 6(S - 30) = 0\\[1em] \Rightarrow (S - 30)(S - 6) = 0\\[1em] \Rightarrow (S - 30) = 0 \text{ or } (S - 6) = 0\\[1em] \Rightarrow S = 30 \text{ or } S = 6\\[1em]$

Substituting the value of S in equation, L = S - 10

⇒ L = 30 - 10 = 20 or 6 - 10 = -4

As time cannot be negative.

Hence, pipe of the larger diameter alone will take 20 hours to fill the pool.

Two years ago the ages of Radha and Meena were in the ratio 5 : 2. If the sum of their present ages is 39 years, their ages, 2 years ago, were :

1. 27 years and 12 years

2. 17 years and 22 years

3. 25 years and 10 years

4. 11 years and 28 years

Answer

Let present ages of Radha and Meena be x and y years respectively.

Given,

Sum of present ages = 39

⇒ x + y = 39

⇒ x = 39 - y ........(1)

Given,

Two years ago the ages of Radha and Meena were in the ratio 5 : 2.

$\Rightarrow \dfrac{x - 2}{y - 2} = \dfrac{5}{2} \\[1em] \Rightarrow \dfrac{39 - y - 2}{y - 2} = \dfrac{5}{2} \\[1em] \Rightarrow \dfrac{37 - y}{y - 2} = \dfrac{5}{2} \\[1em] \Rightarrow 2(37 - y) = 5(y - 2) \\[1em] \Rightarrow 74 - 2y = 5y - 10 \\[1em] \Rightarrow 5y + 2y = 74 + 10 \\[1em] \Rightarrow 7y = 84 \\[1em] \Rightarrow y = \dfrac{84}{7} = 12.$

x = 39 - y = 39 - 12 = 27.

∴ Radha's ages = 27 years and Meena's age = 12 years.

Two years ago their age will be :

x - 2 = 27 - 2 = 25 years and y - 2 = 12 - 2 = 10 years.

Hence, Option 3 is the correct option.

The perimeter of a rectangular field is 28 m and its area is 40 sq. m. Its sides are :

1. 8 m and 6 m

2. 4 m and 10 m

3. 10 m and 6 m

4. 3 m and 11 m

Answer

Let length and breadth of rectangular field be l and b meters respectively.

By formula,

⇒ Perimeter = 2(l + b)

⇒ 28 = 2(l + b)

⇒ l + b = 14

⇒ l = 14 - b ......(1)

By formula,

⇒ Area = lb

⇒ 40 = lb

Substituting value of l from equation (1), we get :

⇒ 40 = b(14 - b)

⇒ 40 = 14b - b²

⇒ b² - 14b + 40 = 0

⇒ b² - 10b - 4b + 40 = 0

⇒ b(b - 10) - 4(b - 10) = 0

⇒ (b - 4)(b - 10) = 0

⇒ b - 4 = 0 or b - 10 = 0

⇒ b = 4 or b = 10.

If b = 4,

l = 14 - b = 14 - 4 = 10.

If b = 10,

l = 14 - b = 14 - 10 = 4.

∴ Sides = 4 m and 10 m.

Hence, Option 2 is the correct option.

The perimeter of a square is numerically equal to its area. The perimeter of the square is :

1. 4 units

2. 8 units

3. 12 units

4. 16 units

Answer

Let side of square be x units.

Given,

Area = Perimeter

⇒ (side)² = 4 × side

⇒ x² = 4x

⇒ x² - 4x = 0

⇒ x(x - 4) = 0

⇒ x = 0 or x - 4 = 0

⇒ x = 0 or x = 4.

Since, side cannot be equal to zero.

∴ Side = 4 units

Perimeter = 4 × 4 = 16 units.

Hence, Option 4 is the correct option.

If the width of the uniform shaded portion is x m; its area in terms of x is :

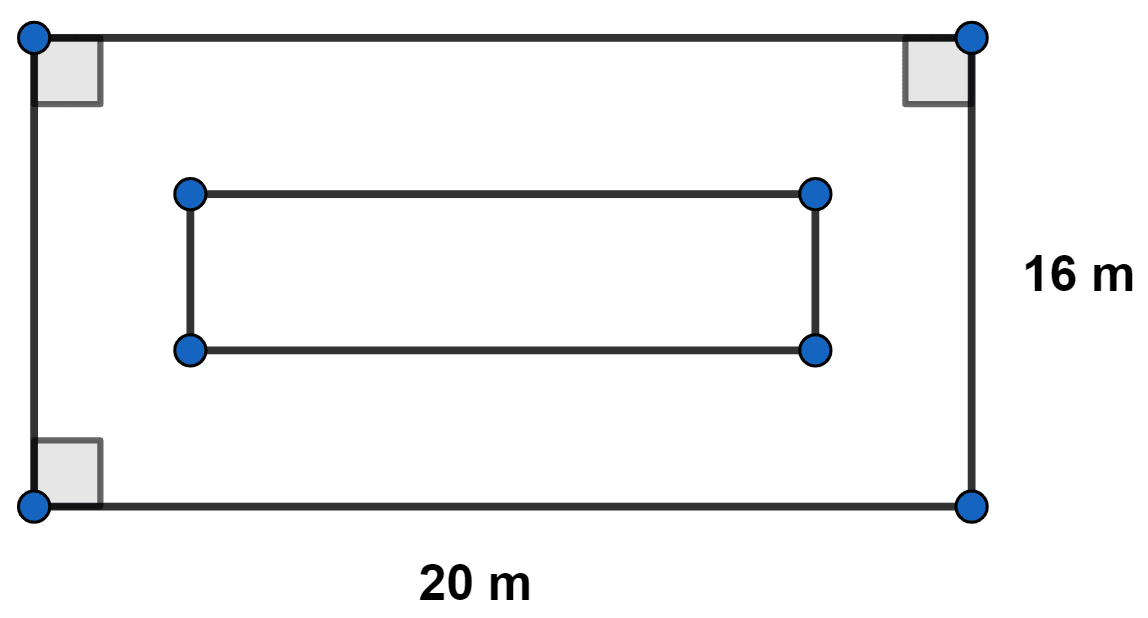
1. 320 m² - (16 - 2x)(20 - 2x) m²

2. 320 m² - (16 - x)(20 - x) m²

3. 320 m² - (16 - 2x)(20 - x) m²

4. 320 m² - (16 - x)(20 - 2x) m²

Answer

From figure,

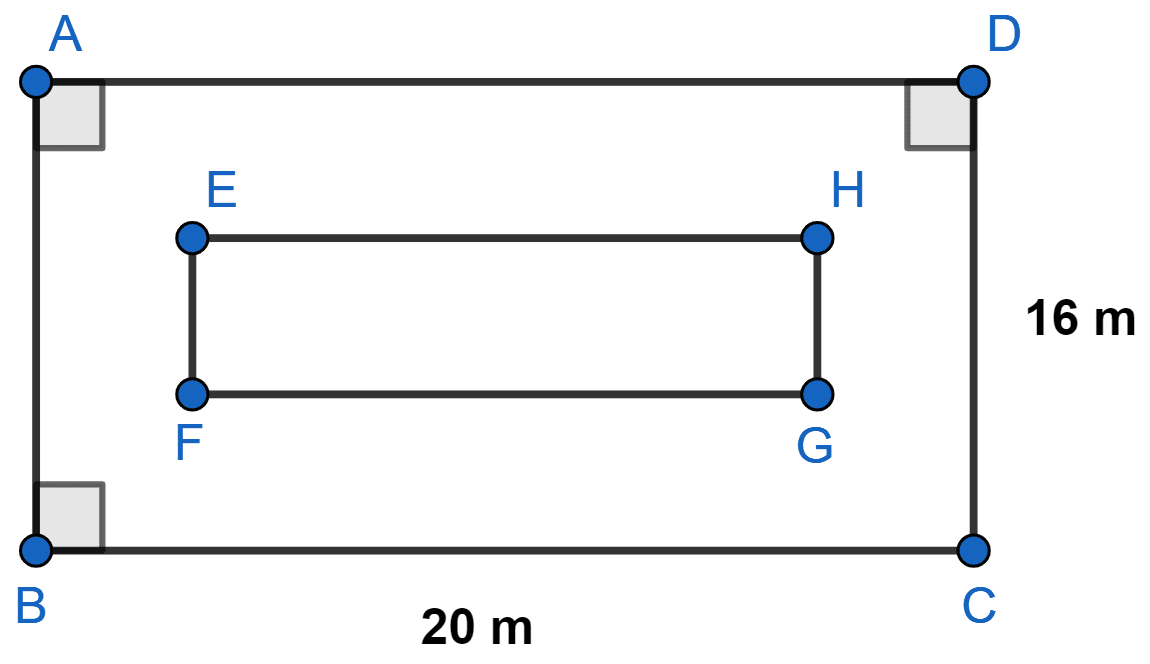
EF = 16 - x - x = (16 - 2x) meters

FG = 20 - x - x = (20 - 2x) meters

Area of shaded portion = Area of rectangle ABCD - Area of rectangle EFGH

= AB × BC - EF × FG

= 16 × 20 - (16 - 2x)(20 - 2x)

= 320 m² - (16 - 2x)(20 - 2x) m².

Hence, Option 1 is the correct option.

The speed of a boat is 32 km/h. If the speed of stream is 8 km/h, the speed of the boat upstream is :

1. 36km/h

2. 40 km/h

3. 16 km/h

4. 24 km/h

Answer

Speed of boat upstream = Speed of boat - Speed of stream

= 32 km/h - 8 km/h

= 24 km/h

Hence, Option 4 is the correct option.

The speed of train A is x km/hr and speed of train B is (x - 5) km/h. How much time will each train take to cover 400 km ?

1. $\dfrac{x}{400} \text{ hrs and } \dfrac{x - 5}{400}$ hrs

2. x × 400 hrs and (x - 5) × 400 hrs

3. $\dfrac{400}{x} \text{ hrs and } \dfrac{400}{x - 5}$ hrs

4. $\dfrac{800}{x(x - 5)}$ hrs

Answer

By formula,

Time = $\dfrac{\text{Distance}}{\text{Speed}}$

For train A :

Time taken = $\dfrac{400}{x}$ hrs.

For train B :

Time taken = $\dfrac{400}{x - 5}$ hrs.

Hence, Option 3 is the correct option.

A boy is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages.

Answer

Let the age of sister be x years.

It is given in question that the boy is twice as old as her sister.

⇒ Boy's age = 2x

Four years hence, the product of their ages = 160

⇒ (Sister's age + 4) x (Boy's age + 4) = 160

⇒ (x + 4) $\times$ (2x + 4) = 160

⇒ x $\times$ (2x + 4) + 4 $\times$ (2x + 4) = 160

⇒ 2x² + 4x + 8x + 16 = 160

⇒ 2x² + 12x + 16 - 160 = 0

⇒ 2x² + 12x - 144 = 0

⇒ x² + 6x - 72 = 0

⇒ x² + 12x - 6x - 72 = 0

⇒ x(x + 12) - 6(x + 12) = 0

⇒ (x + 12)(x - 6) = 0

⇒ (x + 12) = 0 or (x - 6) = 0

⇒ x = -12 or x = 6

Since age cannot be negative,

∴ Present age of sister = 6 years

Boy's age = 2 x 6 = 12 years

Thus, the present age of boy = 12 years and sister = 6 years.

Seven years ago, Rohit's age was five times the square of Geeta's age. 3 years hence, Geeta's age will be two fifths of Rohit's age. Find their ages.

Answer

Let the age of Geeta be x years and that of Rohit be y years.

It is given that 7 years ago, Rohit's age was five times the square of Geeta's age.

⇒ y - 7 = 5(x - 7)²

⇒ y - 7 = 5(x² + 49 - 14x)

⇒ y - 7 = 5x² + 245 - 70x

⇒ y = 5x² + 245 - 70x + 7

⇒ y = 5x² + 252 - 70x .......... (1)

And, 3 years hence, Geeta's age will be two fifths of Rohit's age.

⇒ (x + 3) = $\dfrac{2}{5}$ (y + 3)

⇒ 5(x + 3) = 2(y + 3)

⇒ 5x + 15 = 2y + 6

⇒ 5x + 15 - 6 = 2y

⇒ 5x + 9 = 2y .......... (2)

Substituting the value of y in the above equation,

⇒ 5x + 9 = 2(5x² + 252 - 70x)

⇒ 5x + 9 = 10x² + 504 - 140x

⇒ 10x² + 504 - 140x - 5x - 9 = 0

⇒ 10x² - 145x + 495 = 0

⇒ 2x² - 29x + 99 = 0

⇒ 2x² - 18x - 11x + 99 = 0

⇒ 2x(x - 9) - 11(x - 9) = 0

⇒ (x - 9)(2x - 11) = 0

⇒ (x - 9) = 0 or (2x - 11) = 0

⇒ x = 9 or 2x = 11

⇒ x = 9 or x = $\dfrac{11}{2}$

Since, age cannot be in fraction. So, the age of Geeta = 9 years.

Substituting the value of x in equation (2),

⇒ 5 $\times$ 9 + 9 = 2y

⇒ 45 + 9 = 2y

⇒ 54 = 2y

⇒ y = $\dfrac{54}{2}$ = 27

Thus, the age of Rohit = 27 years and that of Geeta = 9 years.

The sum of the reciprocals of Joseph's age 3 years ago and five years from now is $\dfrac{1}{3}$. Find his present age.

Answer

Let present age of Joseph be x years.

It is given that the sum of the reciprocals of Joseph's age 3 years ago and five years from now is $\dfrac{1}{3}$.

$\Rightarrow \dfrac{1}{x - 3} + \dfrac{1}{x + 5} = \dfrac{1}{3}\\[1em] \Rightarrow \dfrac{(x + 5) + (x - 3)}{(x - 3)(x + 5)} = \dfrac{1}{3}\\[1em] \Rightarrow \dfrac{2x + 2}{(x - 3)(x + 5)} = \dfrac{1}{3}\\[1em] \Rightarrow 3(2x + 2) = (x - 3)(x + 5)\\[1em] \Rightarrow 6x + 6 = x(x + 5) - 3(x + 5)\\[1em] \Rightarrow 6x + 6 = x^2 + 5x - 3x - 15\\[1em] \Rightarrow x^2 + 5x - 3x - 15 - 6x - 6 = 0\\[1em] \Rightarrow x^2 - 4x - 21 = 0\\[1em] \Rightarrow x^2 - 7x + 3x - 21 = 0\\[1em] \Rightarrow x(x - 7) + 3(x - 7) = 0\\[1em] \Rightarrow (x - 7)(x + 3) = 0\\[1em] \Rightarrow (x - 7) = 0 \text{ or } (x + 3) = 0\\[1em] \Rightarrow x = 7 \text{ or } x = -3\\[1em]$

Since, age cannot be negative.

Hence, the present age of Joseph = 7 years.

The diagonal of a rectangular field is 16 m more than the shorter side. If the longer side is 14 m more than the shorter side, find the length and the breadth of the rectangular field.

Answer

Let the shorter side of the rectangular field be x m.

It is given that the diagonal of a rectangular field is 16 m more than the shorter side.

⇒ d = x + 16

And, the longer side is 14 m more than the shorter side.

⇒ l = x + 14

As we know that angles of rectangle are 90°. Using Pythagoras theorem,

⇒ diagonal² = length² + breadth²

⇒ (x + 16)² = (x + 14)² + x²

⇒ x² + 16² + 32x = x² + 14² + 28x + x²

⇒ x² + 256 + 32x = 2x² + 196 + 28x

⇒ 2x² + 196 + 28x - x² - 256 - 32x = 0

⇒ x² - 4x - 60 = 0

⇒ x² - 10x + 6x - 60 = 0

⇒ x(x - 10) + 6(x - 10) = 0

⇒ (x - 10)(x + 6) = 0

⇒ (x - 10) = 0 or (x + 6) = 0

⇒ x = 10 or x = -6

As length of shorter side cannot be negative,

Length = 10 + 14 = 24 m

Hence, length and breath of the rectangle = 24 m and 10 m.

Sum of the areas of two squares is 260 m². If the difference of their perimeters is 24 m, find the sides of the two squares.

Answer

Let the sides of two squares be 'a' m and 'b' m.

As we know that area of square = (side)² and perimeter of square = 4 x side

It is given that sum of the areas of two squares is 260 m².

⇒ a² + b² = 260 .......... (1)

And, the difference of their perimeters is 24 m.

⇒ 4a - 4b = 24

⇒ 4(a - b) = 24

⇒ a - b = $\dfrac{24}{4}$

⇒ a - b = 6

⇒ a = 6 + b .......... (2)

Substituting the value of a in equation (1), we get

⇒ (6 + b)² + b² = 260

⇒ 36 + b² + 12b + b² = 260

⇒ 36 + 2b² + 12b - 260 = 0