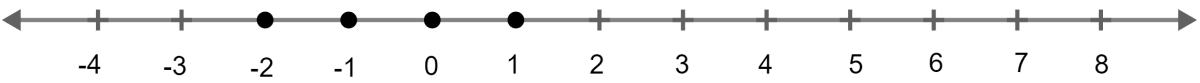Linear Inequations (In one variable)

For the replacement set = {-8, -6, -4, -2, 0, 2, 4, 6, 8}, which of the following is not a solution set ?

1. {-8, -6, -5, -4, 6}

2. {-6, -2, 0, 2, 6}

3. {-8, -4, -2, 0, 2}

4. {-2, 0, 4, 8}

Answer

For the replacement set = {-8, -6, -4, -2, 0, 2, 4, 6, 8}.

{-8, -6, -5, -4, 6} is not the solution set as the element -5 is not present in replacement set.

Hence, Option 1 is the correct option.

The value of x, for 4(2x - 5) < 2x + 28, x ∈ R, is :

1. x > 8

2. x < 8

3. x > -8

4. x < -8

Answer

Given,

⇒ 4(2x - 5) < 2x + 28

⇒ 8x - 20 < 2x + 28

⇒ 8x - 2x < 28 + 20

⇒ 6x < 48

⇒ x < $\dfrac{48}{6}$

⇒ x < 8.

Hence, Option 2 is the correct option.

The solution set for the inequation -2x + 7 ≤ 3, x ∈ R is :

1. {x : x ∈ R, x < 2}

2. {x : x ∈ R, x > 2}

3. {x : x ∈ R, x ≤ 2}

4. {x : x ∈ R, x ≥ 2}

Answer

Given,

⇒ -2x + 7 ≤ 3

⇒ 2x ≥ 7 - 3

⇒ 2x ≥ 4

⇒ x ≥ $\dfrac{4}{2}$

⇒ x ≥ 2.

Since, x ∈ R.

Solution set = {x : x ∈ R, x ≥ 2}

Hence, Option 4 is the correct option.

For 7 - 3x < x - 5, the solution set is :

1. x > 3

2. x < 3

3. x ≥ 3

4. x ≤ 3

Answer

Given,

⇒ 7 - 3x < x - 5

⇒ x + 3x > 7 + 5

⇒ 4x > 12

⇒ x > $\dfrac{12}{4}$

⇒ x > 3.

Hence, Option 1 is the correct option.

x(8 - x) > 0 and x ∈ N gives :

1. 0 ≤ x < 8

2. 1 < x ≤ 8

3. 0 < x < 8

4. 0 ≤ x ≤ 8

Answer

For x(8 - x) > 0

Either,

⇒ x > 0 and (8 - x) > 0

⇒ x > 0 and x < 8 ...........(1)

or,

⇒ x < 0 and (8 - x) < 0

⇒ x < 0 and x > 8 .............(2)

But both conditions of equation (2) are not possible simultaneously.

From equation (1),

Solution set = {0 < x < 8}.

Hence, Option 3 is the correct option.

State, true or false :

(i) x < -y ⇒ -x > y

(ii) -5x ≥ 15 ⇒ x ≥ -3

(iii) 2x ≤ -7 ⇒ $\dfrac{2x}{-4} \ge \dfrac{-7}{-4}$

(iv) 7 > 5 ⇒ $\dfrac{1}{7} \lt \dfrac{1}{5}$

Answer

(i) Given,

x < -y

∴ -x > y [Using rule 5]

Hence, the statement is True.

(ii) Given,

-5x ≥ 15

Dividing both sides of the above inequation by -5,

⇒ x ≤ -3 [Using rule 4]

Hence, the statement is False.

(iii) Given,

2x ≤ -7

Dividing both sides of the above inequation by -4,

⇒ $\dfrac{2x}{-4} \ge \dfrac{-7}{-4}$ [Using rule 4]

Hence, the statement is True.

(iv) Given,

7 > 5

Taking reciprocals,

$\dfrac{1}{7} \lt \dfrac{1}{5}$ [Using rule 6]

Hence, the statement is True.

State, whether the following statements are true or false.

(i) If a < b, then a - c < b - c

(ii) If a > b, then a + c > b + c

(iii) If a < b, then ac > bc

(iv) If a > b, then $\dfrac{a}{c} \lt \dfrac{b}{c}$

(v) If a - c > b - d; then a + d > b + c

(vi) If a < b, and c > 0, then a - c > b - c

where a, b, c, and d are real numbers c ≠ 0.

Answer

(i) Given,

a < b

Subtracting both sides by c,

a - c < b - c.

Hence, the statement is True.

(ii) Given,

a > b

Adding both sides by c,

a + c > b + c.

Hence, the statement is True.

(iii) Given,

a < b

If c is a positive number,

Multiplying both sides by c we get,

ac < bc

If c is a negative number,

Multiplying both sides by c we get,

ac > bc [Using rule 4]

Hence, the statement is False.

(iv) Given,

a > b

If c is a positive number,

Dividing both sides by c we get,

$\dfrac{a}{c} \gt \dfrac{b}{c}$

If c is a negative number,

Dividing both sides by c we get,

$\dfrac{a}{c} \lt \dfrac{b}{c}$ [Using rule 4]

Hence, the statement is False.

(v) Given,

a - c > b - d

Adding both sides by (c + d) we get,

⇒ a - c + (c + d) > b - d + (c + d)

⇒ a - c + c + d > b + c - d + d

⇒ a + d > b + c

Hence, the statement is True.

(vi) Given,

a < b and c > 0

Subtracting both sides by c we get,

a - c < b - c [As c is a positive number.]

Hence, the statement is False.

If x ∈ N, find the solution set of inequations.

(i) 5x + 3 ≤ 2x + 18

(ii) 3x - 2 < 19 - 4x

Answer

(i) 5x + 3 ≤ 2x + 18

⇒ 5x - 2x ≤ 18 - 3

⇒ 3x ≤ 15

Dividing both sides by 3

⇒ x ≤ 5

Since, x ∈ N

∴ Solution set = {1, 2, 3, 4, 5}.

(ii) 3x - 2 < 19 - 4x

⇒ 3x + 4x < 19 + 2

⇒ 7x < 21

Dividing both sides by 7 we get,

⇒ x < 3

Since, x ∈ N

∴ Solution set = {1, 2}.

If the replacement set is the set of whole numbers, solve :

(i) x + 7 ≤ 11

(ii) 3x - 1 > 8

(iii) 8 - x > 5

(iv) 7 - 3x ≥ $-\dfrac{1}{2}$

Answer

(i) x + 7 ≤ 11

⇒ x ≤ 11 - 7

⇒ x ≤ 4

Since, x ∈ W

∴ Solution set = {0, 1, 2, 3, 4}.

(ii) 3x - 1 > 8

⇒ 3x > 8 + 1

⇒ 3x > 9

Dividing both sides by 3 we get,

⇒ x > 3

Since, x ∈ W

∴ Solution set = {4, 5, 6, ........}.

(iii) 8 - x > 5

⇒ -x > 5 - 8

⇒ -x > -3

Multiplying both sides by (-1) we get,

⇒ x < 3 (As on multiplying by negative no. the sign reverses.)

Since, x ∈ W

∴ Solution set = {0, 1, 2}.

(iv) 7 - 3x ≥ $-\dfrac{1}{2}$

⇒ -3x ≥ $-\dfrac{1}{2} - 7$

⇒ -3x ≥ $-\dfrac{15}{2}$

Dividing both sides by (-3) we get,

⇒ x ≤ $\dfrac{5}{2}$ (As on dividing by negative no. the sign reverses.)

Since, x ∈ W

∴ Solution set = {0, 1, 2}.

Solve the inequation :

3 - 2x ≥ x - 12 given that x ∈ N.

Answer

Given,

⇒ 3 - 2x ≥ x - 12

⇒ x + 2x ≤ 3 + 12

⇒ 3x ≤ 15

Dividing both sides by 3 we get,

⇒ x ≤ 5

Since, x ∈ N

∴ Solution set = {1, 2, 3, 4, 5}.

If 25 - 4x ≤ 16, find :

(i) the smallest value of x when x is a real number,

(ii) the smallest value of x when x is an integer.

Answer

Given,

⇒ 25 - 4x ≤ 16

⇒ -4x ≤ 16 - 25

⇒ -4x ≤ -9

Multiplying both sides by -1 we get,

⇒ 4x ≥ 9 (As on multiplying by negative no. the sign reverses.)

Dividing both sides by 4 we get,

⇒ x ≥ $\dfrac{9}{4}$

⇒ x ≥ 2.25

(i) Given,

x ≥ 2.25

Hence, smallest value of x when x is a real number is 2.25

(ii) Given,

x ≥ 2.25

Hence, smallest value of x when x is an integer is 3.

If the replacement set is the set of real numbers, solve :

(i) -4x ≥ -16

(ii) 8 - 3x ≤ 20

Answer

(i) -4x ≥ -16

$\Rightarrow \dfrac{-4x}{-4} \le \dfrac{-16}{-4} \\[1em] \Rightarrow x \le 4$

∴ Solution set = {x : x ∈ R and x ≤ 4}

(ii) 8 - 3x ≤ 20

⇒ -3x ≤ 20 - 8

⇒ -3x ≤ 12

Dividing both sides by -3 we get.

⇒ x ≥ -4 (As on dividing by negative no. the sign reverses.)

∴ Solution set = {x : x ∈ R and x ≥ -4}.

Find the smallest value of x for which 5 - 2x < $5\dfrac{1}{2} - \dfrac{5}{3}x$, where x is an integer.

Answer

Given,

$\Rightarrow 5 - 2x \lt 5\dfrac{1}{2} - \dfrac{5}{3}x \\[1em] \Rightarrow 5 - 2x \lt \dfrac{11}{2} - \dfrac{5}{3}x \\[1em] \Rightarrow 5 - \dfrac{11}{2} \lt -\dfrac{5}{3}x + 2x \\[1em] \Rightarrow \dfrac{10 - 11}{2} \lt \dfrac{-5x + 6x}{3} \\[1em] \Rightarrow -\dfrac{1}{2} \lt \dfrac{x}{3} \\[1em] \Rightarrow \dfrac{x}{3} \times 3 \gt -\dfrac{1}{2} \times 3 \\[1em] \Rightarrow x \gt -\dfrac{3}{2} \\[1em] \Rightarrow x \gt -1.5$

Since, x is an integer.

Hence, smallest value of x = -1.

Find the largest value of x for which

2(x - 1) ≤ 9 - x and x ∈ W.

Answer

Given,

⇒ 2(x - 1) ≤ 9 - x

⇒ 2x - 2 ≤ 9 - x

⇒ 2x + x ≤ 9 + 2

⇒ 3x ≤ 11

⇒ x ≤ $\dfrac{11}{3}$

⇒ x ≤ 3.67

Since, x ∈ W

Hence, largest value of x for which 2(x - 1) ≤ 9 - x is 3.

For the following real number line, the solution set is :

1. {x : x ∈ W and -2 ≤ x < 4}

2. {x : x ∈ N and -2 ≤ x ≤ -4}

3. {x : x ∈ R and -2 < x ≤ 4}

4. {x : x ∈ R and -2 ≤ x < 4}

Answer

From real number line, we get :

x ∈ R, x > -2 and x ≤ 4.

∴ Solution set = {x : x ∈ R and -2 < x ≤ 4}.

Hence, Option 3 is the correct option.

The solution set for the following number line is :

1. {x : x ∈ Z and -3 < x < 4}

2. {x : x ∈ Z and -3 ≤ x}

3. {x : x ∈ Z and -2 ≤ x ≤ 4}

4. {x : x ∈ Z and -3 ≤ x ≤ 4}

Answer

From number line :

x ∈ Integers (Z) and x ≥ -3.

Solution set = {x : x ∈ Z and -3 ≤ x}.

Hence, Option 2 is the correct option.

The following number line represents :

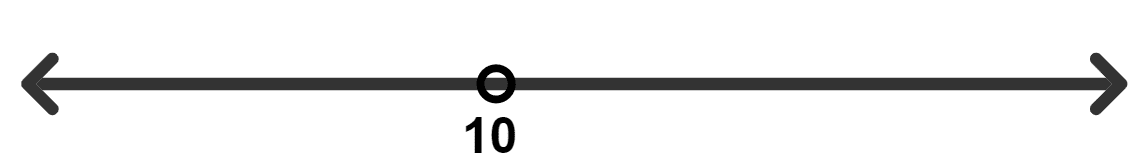
1. {x : x ∈ R and x = 10}

2. {(x < 10) ∪ (x > 10)}

3. {(10 > x) ∩ (x > 10)}

4. {x : x ∈ R and x < 10}

Answer

From the number line, we get :

Solution set = {{(x < 10) ∪ (x > 10)}}

Hence, Option 2 is the correct option.

The solution set for the following number line is :

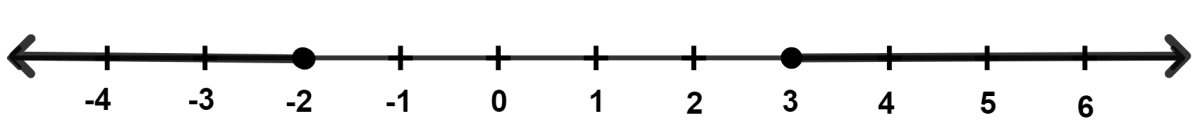
1. {x : x ∈ R, x < -2 and x > 3}

2. {x : x ∈ R and -2 < x < 3}

3. {x : x ∈ R, x < -2 or x < 3}

4. {x : x ∈ R, x ≤ -2 or x ≥ 3}

Answer

From number line, we get :

x ∈ R, x < -2 or x > 3.

∴ Solution set = {x : x ∈ R, x < -2 or x > 3}

Hence, Option 4 is the correct option.

The number line for the solution of inequation x > 5 and x < 10 (x ∈ R) is :

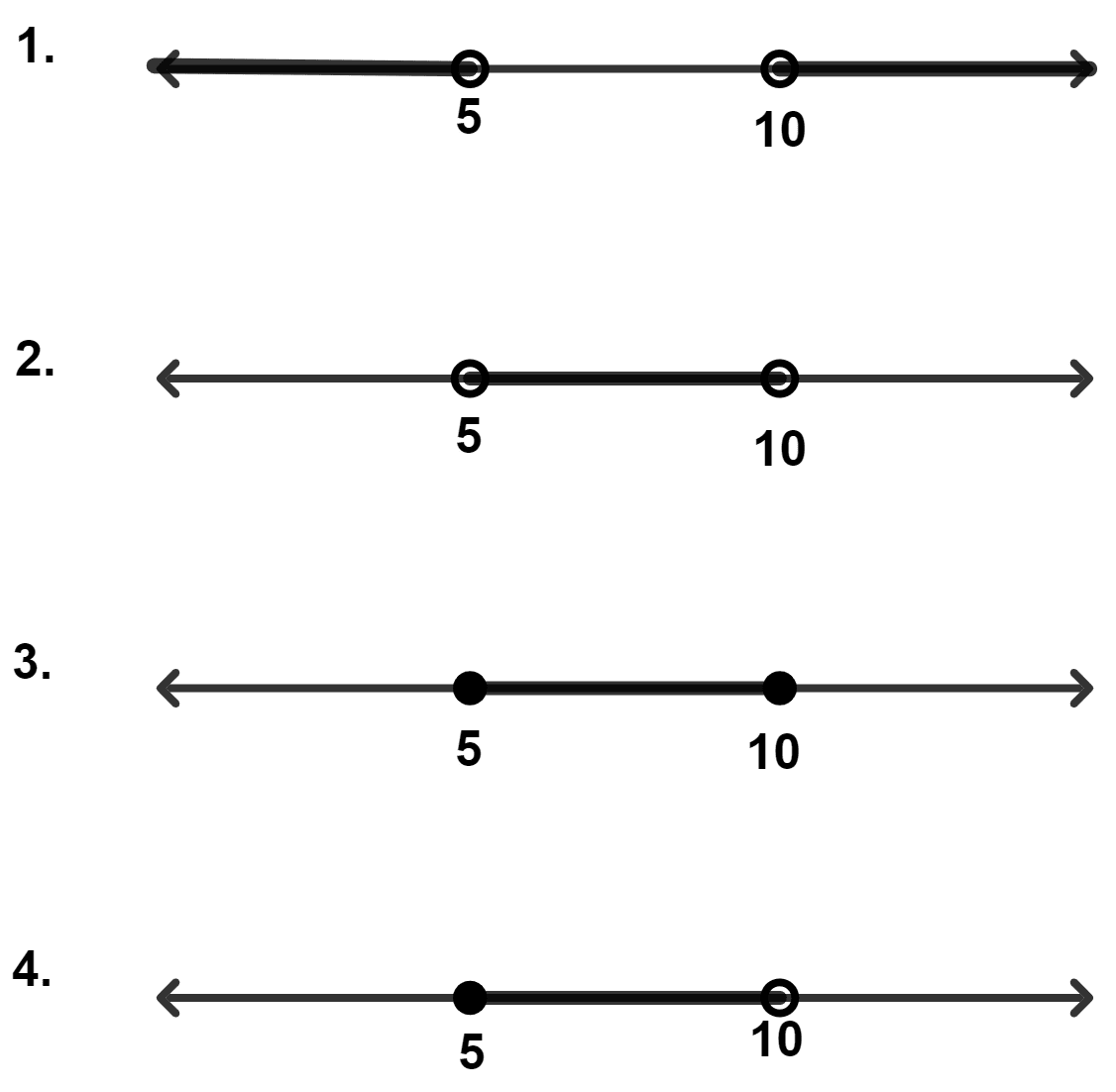
Answer

For x > 5, x < 10 and x ∈ R.

Solution set = {x : x ∈ R and 5 < x < 10}.

Hence, Option 2 is the correct option.

Represent the following inequalities on real number lines :

(i) 2x - 1 < 5

(ii) 3x + 1 ≥ -5

(iii) 2(2x - 3) ≤ 6

(iv) -4 < x < 4

(v) -2 ≤ x < 5

(vi) 8 ≥ x > -3

(vii) -5 < x ≤ -1

Answer

(i) 2x - 1 < 5

⇒ 2x < 5 + 1

⇒ 2x < 6

⇒ x < 3

Solution on the number line is :

(ii) 3x + 1 ≥ -5

⇒ 3x ≥ -5 - 1

⇒ 3x ≥ -6

Dividing both sides by 3 we get,

⇒ x ≥ -2

Solution on the number line is :

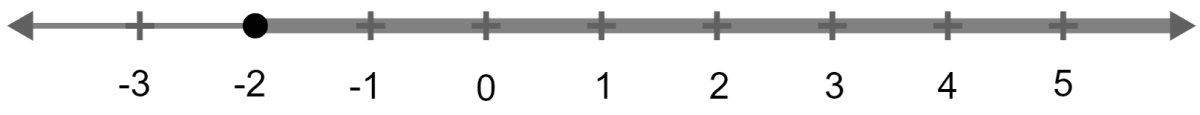
(iii) 2(2x - 3) ≤ 6

⇒ 4x - 6 ≤ 6

⇒ 4x ≤ 6 + 6

⇒ 4x ≤ 12

Dividing both sides by 4 we get,

⇒ x ≤ 3

Solution on the number line is :

(iv) -4 < x < 4

Solution on the number line is :

(v) -2 ≤ x < 5

Solution on the number line is :

(vi) 8 ≥ x > -3

Solution on the number line is :

(vii) -5 < x ≤ -1

Solution on the number line is :

For each graph given alongside, write an inequation taking x as the variable :

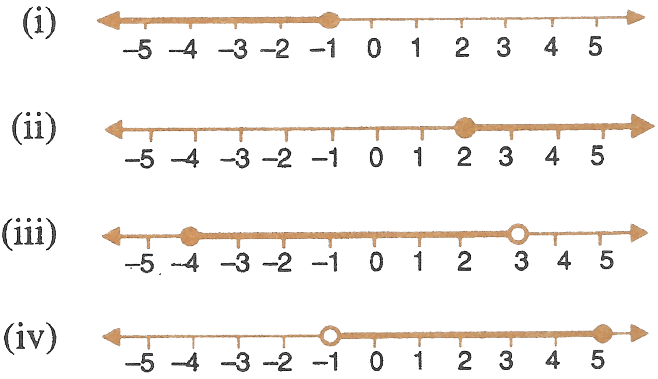
Answer

(i) From graph we get,

x ≤ -1 and x ∈ R.

(ii) From graph we get,

x ≥ 2 and x ∈ R.

(iii) From graph we get,

-4 ≤ x < 3 and x ∈ R.

(iv) From graph we get,

-1 < x ≤ 5 and x ∈ R.

For the following inequations, graph the solution set on the real number line :

-4 ≤ 3x - 1 < 8

Answer

-4 ≤ 3x - 1 < 8

Solving L.H.S. of the equation,

⇒ -4 ≤ 3x - 1

⇒ 3x ≥ -4 + 1

⇒ 3x ≥ -3

⇒ x ≥ -1 .........(i)

Solving R.H.S. of the equation,

⇒ 3x - 1 < 8

⇒ 3x < 8 + 1

⇒ 3x < 9

⇒ x < 3 .........(ii)

From (i) and (ii) we get,

-1 ≤ x < 3.

∴ Solution set = {-1 ≤ x < 3 : x ∈ R }

Solution on the number line is :

For the following inequations, graph the solution set on the real number line :

x - 1 < 3 - x ≤ 5

Answer

x - 1 < 3 - x ≤ 5

Solving L.H.S. of the equation,

⇒ x - 1 < 3 - x

⇒ x + x < 3 + 1

⇒ 2x < 4

⇒ x < 2 .........(i)

Solving R.H.S. of the equation,

⇒ 3 - x ≤ 5

⇒ x ≥ 3 - 5

⇒ x ≥ -2 .........(ii)

From (i) and (ii) we get,

-2 ≤ x < 2.

∴ Solution set = {-2 ≤ x < 2 : x ∈ R}

Solution on the number line is :

Represent the solution set of each of the following inequalities on the real number line :

4x - 1 > x + 11

Answer

Given,

⇒ 4x - 1 > x + 11

⇒ 4x - x > 11 + 1

⇒ 3x > 12

Dividing both sides by 3 we get,

⇒ x > 4.

∴ Solution set = {x : x ∈ R and x > 4}.

Solution on the number line is :

Represent the solution set of each of the following inequalities on the real number line :

7 - x ≤ 2 - 6x

Answer

Given,

⇒ 7 - x ≤ 2 - 6x

⇒ -x + 6x ≤ 2 - 7

⇒ 5x ≤ -5

Dividing both sides by 5 we get,

⇒ x ≤ -1.

∴ Solution set = {x : x ∈ R and x ≤ -1}.

Solution on the number line is :

Represent the solution set of each of the following inequalities on the real number line :

x + 3 ≤ 2x + 9

Answer

Given,

⇒ x + 3 ≤ 2x + 9

⇒ x - 2x ≤ 9 - 3

⇒ -x ≤ 6

⇒ x ≥ -6

∴ Solution set = { x ≥ -6 : x ∈ R }.

Solution on the number line is :

Represent the solution set of each of the following inequalities on the real number line :

$\dfrac{2x + 5}{3} \gt 3x - 3$

Answer

Given,

⇒ $\dfrac{2x + 5}{3} \gt 3x - 3$

⇒ 2x + 5 > 3(3x - 3)

⇒ 2x + 5 > 9x - 9

⇒ 9x - 2x < 5 + 9

⇒ 7x < 14

Dividing both sides by 7 we get,

⇒ x < 2

∴ Solution set = { x < 2 : x ∈ R }

Solution on the number line is :

x ∈ {real numbers} and -1 < 3 - 2x ≤ 7, evaluate x and represent it on a number line.

Answer

Given,

-1 < 3 - 2x ≤ 7

Solving L.H.S. of the equation,

⇒ -1 < 3 - 2x

⇒ -1 - 3 < -2x

⇒ -4 < -2x

Dividing both sides by -2 we get,

⇒ 2 > x (As sign reverses on dividing by negative no.)

⇒ x < 2 .........(i)

Solving R.H.S. of the equation,

⇒ 3 - 2x ≤ 7

⇒ 3 - 7 ≤ 2x

⇒ -4 ≤ 2x

Dividing both sides by 2 we get,

⇒ -2 ≤ x

⇒ x ≥ -2 .........(ii)

From (i) and (ii) we get,

-2 ≤ x < 2

∴ Solution set = {x : x ∈ R and -2 ≤ x < 2}

Solution on the number line is :

List the elements of the solution set of inequation -3 < x - 2 ≤ 9 - 2x; x ∈ N.

Answer

Given,

⇒ -3 < x - 2 ≤ 9 - 2x

Solving L.H.S. of the equation,

⇒ -3 < x - 2

⇒ x > -3 + 2

⇒ x > -1 .......(i)

Solving R.H.S. of the equation,

⇒ x - 2 ≤ 9 - 2x

⇒ x + 2x ≤ 9 + 2

⇒ 3x ≤ 11

⇒ x ≤ $\dfrac{11}{3}$ .........(ii)

From (i) and (ii) we get,

⇒ -1 < x ≤ $\dfrac{11}{3}$.

Since, x ∈ N

∴ Solution set = {1, 2, 3}.

Find the range of values of x which satisfies

$-2\dfrac{2}{3} \le x + \dfrac{1}{3} \lt 3\dfrac{1}{3}$, x ∈ R.

Graph these values on number line.

Answer

Given,

$\Rightarrow -2\dfrac{2}{3} \le x + \dfrac{1}{3} \lt 3\dfrac{1}{3} \\[1em] \Rightarrow -\dfrac{8}{3} \le x + \dfrac{1}{3} \lt \dfrac{10}{3} \\[1em]$

Solving L.H.S. of the equation,

$\Rightarrow -\dfrac{8}{3} \le x + \dfrac{1}{3} \\[1em] \Rightarrow x \ge -\dfrac{8}{3} - \dfrac{1}{3} \\[1em] \Rightarrow x \ge -\dfrac{9}{3} \\[1em] \Rightarrow x \ge -3 ........(i)$

Solving R.H.S. of the equation,

$\Rightarrow x + \dfrac{1}{3} \lt \dfrac{10}{3} \\[1em] \Rightarrow x \lt \dfrac{10}{3} - \dfrac{1}{3} \\[1em] \Rightarrow x \lt \dfrac{9}{3} \\[1em] \Rightarrow x \lt 3 ..........(ii)$

From (i) and (ii) we get,

-3 ≤ x < 3.

Solution set = {x : x ∈ R and -3 ≤ x < 3}.

Solution on the number line is :

Find the values of x, which satisfy the inequation :

$-2 \le \dfrac{1}{2} - \dfrac{2x}{3} \le 1\dfrac{5}{6}$, x ∈ N.

Graph the solution on the number line.

Answer

Given,

$\Rightarrow -2 \le \dfrac{1}{2} - \dfrac{2x}{3} \le 1\dfrac{5}{6} \\[1em] \Rightarrow -2 \le \dfrac{3 - 4x}{6} \le \dfrac{11}{6} \\[1em]$

Solving L.H.S. of the equation,

$\Rightarrow -2 \le \dfrac{3 - 4x}{6} \\[1em] \Rightarrow -12 \le 3 - 4x \\[1em] \Rightarrow 4x \le 3 + 12 \\[1em] \Rightarrow x \le \dfrac{15}{4} ........(i)$

Solving R.H.S. of the equation,

$\Rightarrow \dfrac{1}{2} - \dfrac{2x}{3} \le \dfrac{11}{6} \\[1em] \Rightarrow \dfrac{2x}{3} \ge \dfrac{1}{2} - \dfrac{11}{6} \\[1em] \Rightarrow \dfrac{2x}{3} \ge \dfrac{3 - 11}{6} \\[1em] \Rightarrow \dfrac{2x}{3} \ge -\dfrac{8}{6} \\[1em] \Rightarrow x \ge -\dfrac{8}{6} \times \dfrac{3}{2} \\[1em] \Rightarrow x \ge -2 .........(ii)$

From (i) and (ii) we get,

$-2 \le x \le \dfrac{15}{4}$

Since, x ∈ N,

∴ Solution set = {1, 2, 3}.

Solution on the number line is :

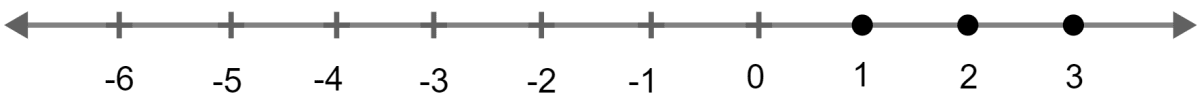
Given x ∈ {real numbers}, find the range of values of x for which -5 ≤ 2x - 3 < x + 2 and represent it on a real number line.

Answer

Given,

-5 ≤ 2x - 3 < x + 2

Solving L.H.S. of the equation,

⇒ -5 ≤ 2x - 3

⇒ 2x ≥ -5 + 3

⇒ 2x ≥ -2

Dividing both sides by 2 we get,

⇒ x ≥ -1 ........(i)

Solving R.H.S. of the equation,

⇒ 2x - 3 < x + 2

⇒ 2x - x < 2 + 3

⇒ x < 5 ........(ii)

From (i) and (ii) we get,

-1 ≤ x < 5.

∴ Solution set = {x : x ∈ R and -1 ≤ x < 5}.

Solution on the number line is :

If 5x - 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.

Answer

Given,

⇒ 5x - 3 ≤ 5 + 3x ≤ 4x + 2

Solving L.H.S. of the equation,

⇒ 5x - 3 ≤ 5 + 3x

⇒ 5x - 3x ≤ 5 + 3

⇒ 2x ≤ 8

⇒ x ≤ 4 ........(i)

Solving R.H.S. of the equation,

⇒ 5 + 3x ≤ 4x + 2

⇒ 3x - 4x ≤ 2 - 5

⇒ -x ≤ -3

⇒ x ≥ 3 .......(ii)

From (i) and (ii) we get,

3 ≤ x ≤ 4

Comparing above equation with a ≤ x ≤ b we get,

a = 3 and b = 4.

Hence, a = 3 and b = 4.

Solve the following inequation and graph the solution set on the number line :

2x - 3 < x + 2 ≤ 3x + 5; x ∈ R.

Answer

Given,

2x - 3 < x + 2 ≤ 3x + 5

Solving L.H.S. of the equation,

⇒ 2x - 3 < x + 2

⇒ 2x - x < 2 + 3

⇒ x < 5 ...........(i)

Solving R.H.S. of the equation,

⇒ x + 2 ≤ 3x + 5

⇒ x - 3x ≤ 5 - 2

⇒ -2x ≤ 3

⇒ 2x ≥ -3

Dividing both sides by 2 we get,

⇒ x ≥ -1.5 .........(ii)

From (i) and (ii) we get,

-1.5 ≤ x < 5

∴ Solution set = {x : x ∈ R and -1.5 ≤ x < 5}.

Solution on the number line is :

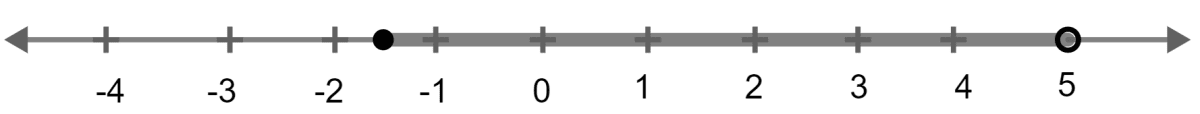
Solve and graph the solution set of :

2x - 9 < 7 and 3x + 9 ≤ 25; x ∈ R.

Answer

Given,

2x - 9 < 7 and 3x + 9 ≤ 25

Solving, 2x - 9 < 7

⇒ 2x < 7 + 9

⇒ 2x < 16

⇒ x < 8 .........(i)

Solving, 3x + 9 ≤ 25

⇒ 3x ≤ 25 - 9

⇒ 3x ≤ 16

⇒ x ≤ $\dfrac{16}{3}$

⇒ x ≤ $5\dfrac{1}{3}$ ........(ii)

From (i) and (ii) we get,

⇒ x ≤ $5\dfrac{1}{3}$

∴ Solution set = {x : x ≤ $5\dfrac{1}{3}$ and x ∈ R}.

Solution on the number line is :

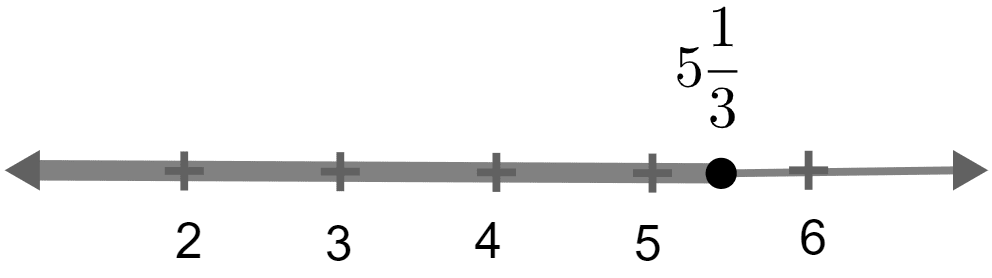
Solve and graph the solution set of :

2x - 9 ≤ 7 and 3x + 9 > 25; x ∈ I

Answer

Given,

2x - 9 ≤ 7 and 3x + 9 > 25

Solving, 2x - 9 ≤ 7

⇒ 2x ≤ 7 + 9

⇒ 2x ≤ 16

⇒ x ≤ 8 .........(i)

Solving, 3x + 9 > 25

⇒ 3x > 25 - 9

⇒ 3x > 16

⇒ x > $\dfrac{16}{3}$

⇒ x > $5\dfrac{1}{3}$ ........(ii)

From (i) and (ii) we get,

⇒ $5\dfrac{1}{3} \lt x \le 8$

Since, x ∈ I,

∴ Solution set = {6, 7, 8}.

Solution on the number line is :

Solve and graph the solution set of :

x + 5 ≥ 4(x - 1) and 3 - 2x < -7; x ∈ R.

Answer

Given,

x + 5 ≥ 4(x - 1) and 3 - 2x < -7

Solving, x + 5 ≥ 4(x - 1)

⇒ x + 5 ≥ 4x - 4

⇒ 4x - x ≤ 5 + 4

⇒ 3x ≤ 9

Dividing both sides by 3 we get,

⇒ x ≤ 3 .......(i)

Solving, 3 - 2x < -7

⇒ 2x > 3 + 7

⇒ 2x > 10

⇒ x > 5 .......(ii)

From (i) and (ii) we get,

x ≤ 3 and x > 5

There is no number possible which is less than or equal to 3 and greater than 5 hence, no solution.

Hence, solution set is an empty set.

Solve and graph the solution set of :

3x - 2 > 19 or 3 - 2x ≥ -7; x ∈ R

Answer

Given,

3x - 2 > 19 or 3 - 2x ≥ -7

Solving, 3x - 2 > 19

⇒ 3x > 19 + 2

⇒ 3x > 21

⇒ x > 7

Solving, 3 - 2x ≥ -7

⇒ 2x ≤ 3 + 7

⇒ 2x ≤ 10

⇒ x ≤ 5.

Hence, x > 7 or x ≤ 5.

Solution on the number line is :

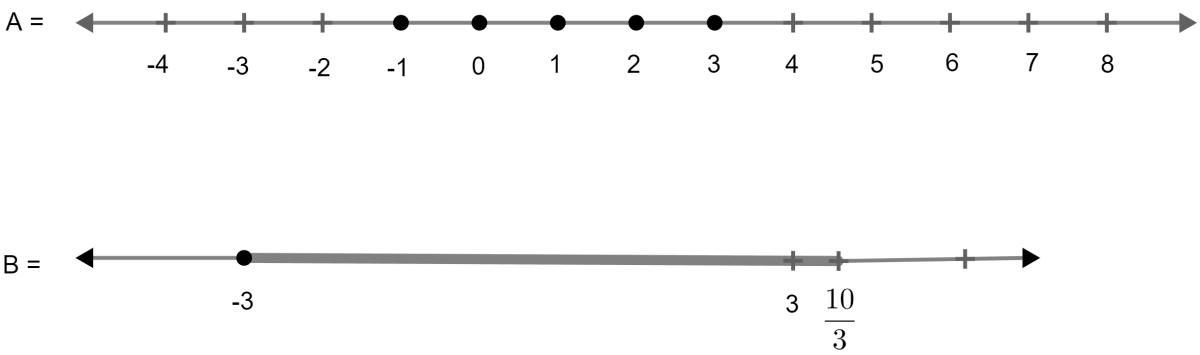
The diagram represents two inequations A and B on a real number lines :

(i) Write down A and B in set builder notation.

(ii) Represent A ∩ B and A ∩ B' on two different number lines.

Answer

(i) A = {x : -2 ≤ x < 5 and x ∈ R}

B = {x : -4 ≤ x < 3 and x ∈ R}

(ii) A ∩ B = Numbers common to both A and B

= {x : -2 ≤ x < 3}

A ∩ B' = Numbers which belong to A but do not belong to B

= {x : 3 ≤ x < 5}

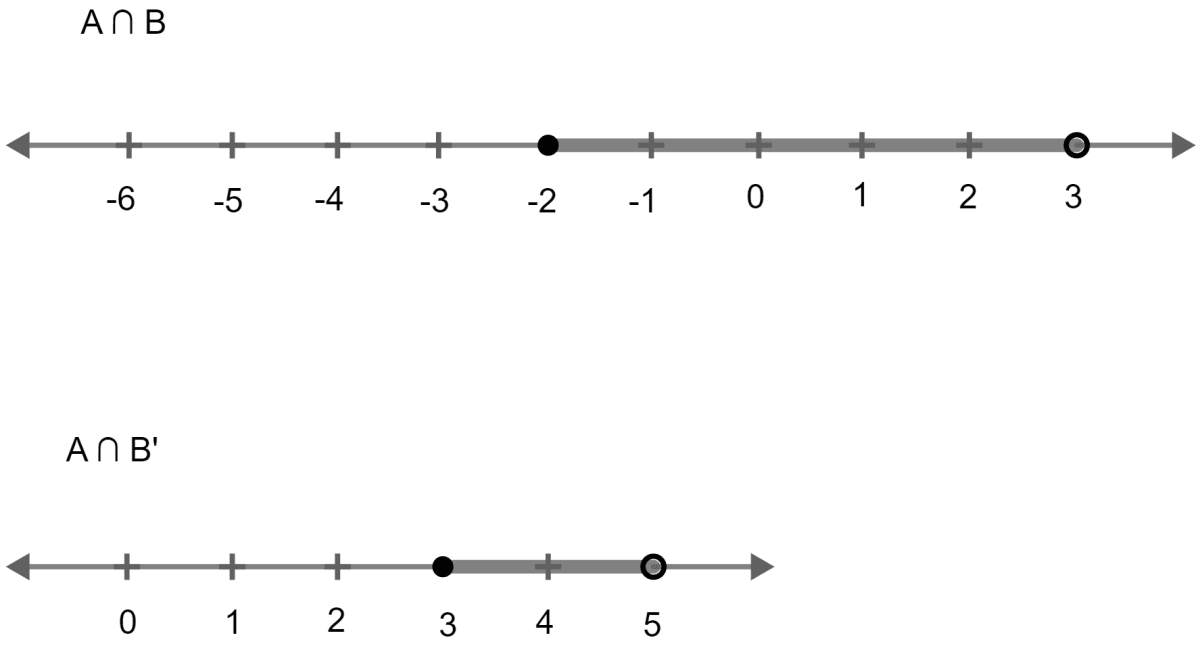
Given A = {x : -1 < x ≤ 5, x ∈ R} and B = {x : -4 ≤ x < 3, x ∈ R}

Represent on different number lines :

(i) A ∩ B

(ii) A' ∩ B

(iii) A - B

Answer

A = {x : -1 < x ≤ 5, x ∈ R} and B = {x : -4 ≤ x < 3, x ∈ R}

(i) A ∩ B = Numbers common to both A and B.

= {x : -1 < x < 3, x ∈ R}

Solution on the number line is :

(ii) A' ∩ B = Numbers which do not belong to A but belong to B

= {x : -4 ≤ x ≤ -1, x ∈ R}

Solution on the number line is :

(iii) A - B = Numbers which belong to A but do not belong to B

= {x : 3 ≤ x ≤ 5}

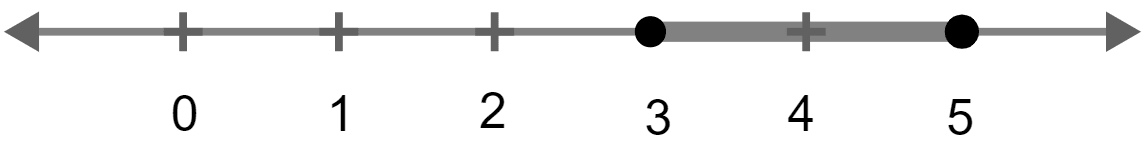
Find the range of values of x, which satisfy :

$-\dfrac{1}{3} \le \dfrac{x}{2} + 1\dfrac{2}{3} \lt 5\dfrac{1}{6}$

Graph, in each of the following cases, the values of x on different real number lines:

(i) x ∈ W

(ii) x ∈ Z

(iii) x ∈ R

Answer

Given,

$\Rightarrow -\dfrac{1}{3} \le \dfrac{x}{2} + 1\dfrac{2}{3} \lt 5\dfrac{1}{6}$

Solving L.H.S of the above equation,

$\Rightarrow -\dfrac{1}{3} \le \dfrac{x}{2} + 1\dfrac{2}{3} \\[1em] \Rightarrow -\dfrac{1}{3} \le \dfrac{x}{2} + \dfrac{5}{3} \\[1em] \Rightarrow \dfrac{x}{2} \ge -\dfrac{1}{3} - \dfrac{5}{3} \\[1em] \Rightarrow \dfrac{x}{2} \ge -\dfrac{6}{3} \\[1em] \Rightarrow \dfrac{x}{2} \ge -2 \\[1em] \Rightarrow x \ge -2 \times 2 \\[1em] \Rightarrow x \ge -4 \space .......(i)$

Solving R.H.S of the above equation,

$\Rightarrow \dfrac{x}{2} + 1\dfrac{2}{3} \lt 5\dfrac{1}{6} \\[1em] \Rightarrow \dfrac{x}{2} + \dfrac{5}{3} \lt \dfrac{31}{6} \\[1em] \Rightarrow \dfrac{x}{2} \lt \dfrac{31}{6} - \dfrac{5}{3} \\[1em] \Rightarrow \dfrac{x}{2} \lt \dfrac{31 - 10}{6} \\[1em] \Rightarrow \dfrac{x}{2} \lt \dfrac{21}{6} \\[1em] \Rightarrow x \lt 2 \times \dfrac{21}{6} \\[1em] \Rightarrow x \lt \dfrac{42}{6} \\[1em] \Rightarrow x \lt 7 \space .......(ii)$

From (i) and (ii) we get,

⇒ -4 ≤ x < 7

(i) In this case x ∈ W

∴ Solution set = {0, 1, 2, 3, 4, 5, 6}

Solution on the number line is :

(ii) In this case x ∈ Z

∴ Solution set = {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}

Solution on the number line is :

(iii) In this case x ∈ R

∴ Solution set = {x : -4 ≤ x < 7, x ∈ R}

Solution on the number line is :

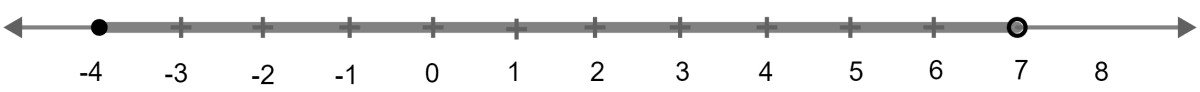
Given : A = {x : -8 < 5x + 2 ≤ 17, x ∈ I}

B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}

Where R = {real numbers} and I = {integers}

Represent A and B on two different numbers lines. Write down elements of A ∩ B.

Answer

Given,

A = {x : -8 < 5x + 2 ≤ 17, x ∈ I}

Solving L.H.S. of the equation,

⇒ -8 < 5x + 2

⇒ 5x > -8 - 2

⇒ 5x > -10

⇒ x > -2 ......(i)

Solving R.H.S. of the equation,

⇒ 5x + 2 ≤ 17

⇒ 5x ≤ 17 - 2

⇒ 5x ≤ 15

⇒ x ≤ 3 .......(ii)

From (i) and (ii) we get,

-2 < x ≤ 3

Since, x ∈ I

∴ Solution set = {-1, 0, 1, 2, 3}

Given,

B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}

Solving L.H.S. of the equation,

⇒ -2 ≤ 7 + 3x

⇒ 3x ≥ -2 - 7

⇒ 3x ≥ -9

⇒ x ≥ -3 .......(iii)

Solving R.H.S. of the equation,

⇒ 7 + 3x < 17

⇒ 3x < 17 - 7

⇒ 3x < 10

⇒ x < $\dfrac{10}{3}$ ........(iv)

From (iii) and (iv) we get,

-3 ≤ x < $\dfrac{10}{3}$

A ∩ B = Elements common to both A and B,

Hence, A ∩ B ={-1, 0, 1, 2, 3}.

Solve the following inequation and represent the solution set on the number line 2x - 5 ≤ 5x + 4 < 11, where x ∈ I.

Answer

Given,

2x - 5 ≤ 5x + 4 < 11

Solving L.H.S. of the equation,

⇒ 2x - 5 ≤ 5x + 4

⇒ 5x - 2x ≥ -5 - 4

⇒ 3x ≥ -9

⇒ x ≥ -3 .......(i)

Solving R.H.S. of the equation,

⇒ 5x + 4 < 11

⇒ 5x < 11 - 4

⇒ 5x < 7

⇒ x < $\dfrac{7}{5}$ .......(ii)

From (i) and (ii) we get,

-3 ≤ x < $\dfrac{7}{5}$

Since, x ∈ I

∴ Solution set = {-3, -2, -1, 0, 1}.

Solution on the number line is :

Given that x ∈ I, solve the inequation and graph the solution on number line :

3 ≥ $\dfrac{x - 4}{2} + \dfrac{x}{3} \ge 2$

Answer

Given,

3 ≥ $\dfrac{x - 4}{2} + \dfrac{x}{3} \ge 2$

Solving L.H.S. of the inequation,

$\Rightarrow 3 \ge \dfrac{x - 4}{2} + \dfrac{x}{3} \\[1em] \Rightarrow \dfrac{3(x - 4) + 2x}{6} \le 3 \\[1em] \Rightarrow 3x - 12 + 2x \le 18 \\[1em] \Rightarrow 5x \le 18 + 12 \\[1em] \Rightarrow 5x \le 30 \\[1em] \Rightarrow x \le 6 ........(i)$

Solving R.H.S. of the inequation,

$\Rightarrow \dfrac{x - 4}{2} + \dfrac{x}{3} \ge 2 \\[1em] \dfrac{3(x - 4) + 2x}{6} \ge 2 \\[1em] 3x - 12 + 2x \ge 12 \\[1em] 5x \ge 24 \\[1em] x \ge \dfrac{24}{5} .......(ii)$

From (i) and (ii) we get,

$\dfrac{24}{5} \le x \le 6$

∴ Solution set = {5, 6}.

Solution on the number line is :

The maximum value of x for the inequation 4x ≤ 12 + x is :

1. 5

2. 4

3. 3

4. 2.4

Answer

Given,

⇒ 4x ≤ 12 + x

⇒ 4x - x ≤ 12

⇒ 3x ≤ 12

⇒ x ≤ $\dfrac{12}{3}$

⇒ x ≤ 4

∴ Maximum value of x will be 4.

Hence, Option 2 is the correct option.

The minimum value of x for the inequation 5x - 4 ≥ 18 - 6x is :

1. 2

2. 22

3. -22

4. -2

Answer

Given,

⇒ 5x - 4 ≥ 18 - 6x

⇒ 5x + 6x ≥ 18 + 4

⇒ 11x ≥ 22

⇒ x ≥ $\dfrac{22}{11}$

⇒ x ≥ 2

∴ Minimum value of x will be 2.

Hence, Option 1 is the correct option.

The value of x for the inequation 3x + 5 < 5x + 13, x ∈ Z is :

1. x > 1

2. x < 1

3. x = 1

4. x ≥ 1

Answer

Given,

⇒ 3x + 5 < 5x + 13

⇒ 5x - 3x > 13 - 5

⇒ 2x > 8

⇒ x > $\dfrac{8}{2}$

⇒ x > 4.

Since, x > 4 so it is also greater than 1.

⇒ x > 1.

Hence, Option 1 is the correct option.

The real number lines for two inequations A and B are as given below, A ∩ B is :

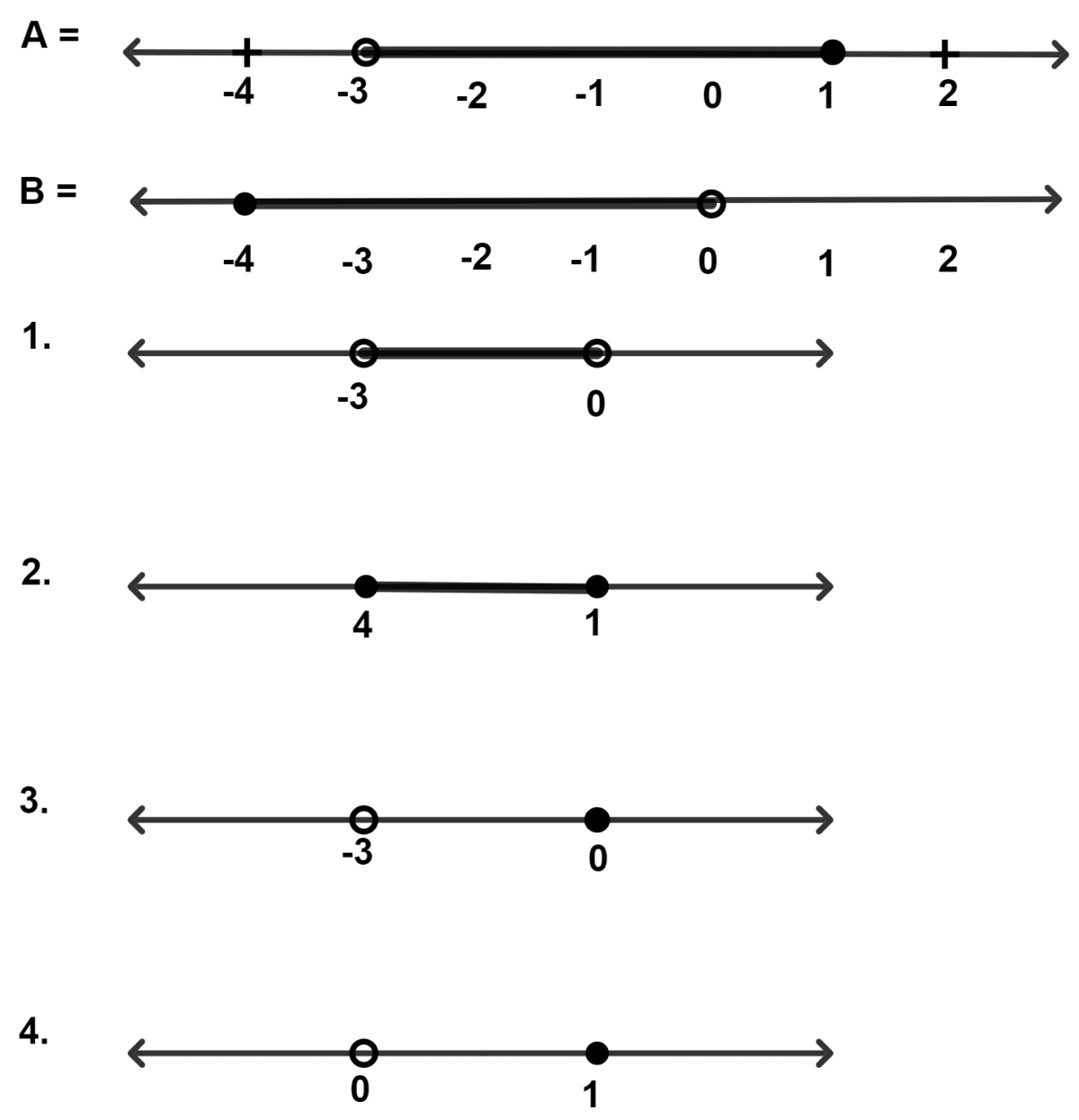
Answer

A = {x : x ∈ R and -3 < x ≤ 1}

B = {x : x ∈ R and -4 ≤ x < 0}

A ∩ B = {x : x ∈ R and -3 < x < 0}

Hence, Option 1 is the correct option.

For the inequations A and B [as given above in part (d)], A ∪ B is :

Answer

A = {x : x ∈ R and -3 < x ≤ 1}

B = {x : x ∈ R and -4 ≤ x < 0}

A ∪ B = {x : x ∈ R and -4 ≤ x ≤ 1}

Hence, Option 1 is the correct option.

$-\dfrac{3}{2} \le -\dfrac{2x}{3}$ where x ∈ R.

Assertion (A): The largest value of x is $\dfrac{9}{4}$.

Reason (R): When the signs of both the sides of an inequalities are changed, the sign of inequality reverses.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is the correct reason for A.

4. Both A and R are true and R is the incorrect reason for A.

Answer

Both A and R are true and R is the correct reason for A.

Reason

According to the assertion:

$\Rightarrow -\dfrac{3}{2} \le -\dfrac{2x}{3}\\[1em] \Rightarrow \dfrac{3}{2} \ge \dfrac{2x}{3}\\[1em] \Rightarrow x \le \dfrac{3 \times 3}{2 \times 2}\\[1em] \Rightarrow x \le \dfrac{9}{4}$

So, Assertion (A) is true.

According to the reason:

When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign must be reversed to maintain the validity of the inequality

So, Reason (R) is true.

Hence, option 3 is correct.

Inequation 5 - 2x ≥ x - 10, where x ∈ N (Natural numbers)

Assertion (A): 5 - 2x ≥ x - 10 ⇒ -3x ≥ -15 ⇒ x ≥ 5

∴ Solution set = {5, 6, 7, 8, ..........}

Reason (R): 5 - 2x ≥ x - 10 ⇒ 5 + 10 ≥ 3x ⇒ x ≤ 5

∴ Solution set = {1, 2, 3, 4, 5}

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

A is false, R is true.

Reason

According to Assertion: 5 - 2x ≥ x - 10

⇒ 5 - 2x + 10 ≥ x

⇒ -2x + 15 ≥ x

⇒ 15 ≥ x + 2x

⇒ 15 ≥ 3x

⇒ x ≤ $\dfrac{15}{3}$

⇒ x ≤ 5

∴ Solution set = {1, 2, 3, 4, 5}

So, Assertion (A) is false.

According to Reason:

Solution set = {1, 2, 3, 4, 5}

So, Reason (R) is true.

Hence, A is false, R is true.

x ∈ W, x ≥ -3 and x < 5.

Statement (1) : There will be no solution for the given inequalities.

Statement (2) : The real number line for the given inequations is :

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Statement 1 is false, and statement 2 is true.

Reason

x ≥ -3

Solution set of x = {-3, -2, -1, 0, 1, 2, ..........} .......... (1)

And, x < 5

Solution set of x = {.........., 1, 2, 3, 4} .......... (2)

From (1) and (2), we get

Solution set = {-3, -2, -1, 0, 1, 2, 3, 4}

So, statement 1 is false.

The real number for the given inequations is :

So, statement 2 is true.

Hence, option 4 is correct.

5 + x ≤ 2x < x - 2, x ∈ R.

Statement (1) : There is no value of x ∈ R that satisfies the given inequation.

Statement (2) : 5 + x - x ≤ 2x - x < x - 2 - x ⇒ 5 ≤ x < -2

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Statement 1 is false, and statement 2 is true.

Reason

Given,

5 + x ≤ 2x

⇒ 5 ≤ 2x - x

⇒ 5 ≤ x .......... (1)

And, 2x < x - 2

⇒ 2x - x < -2

⇒ x < -2 .......... (2)

From (1) and (2), we get

⇒ 5 ≤ x < -2

From solving the above inequation, we get a solution set for x. So, statement 1 is false and statement 2 is true.

Hence, option 4 is correct.

Solve the inequation :

$12 + 1\dfrac{5}{6}x \le 5 + 3x$ and x ∈ R.

Answer

Given,

$\Rightarrow 12 + 1\dfrac{5}{6}x \le 5 + 3x \\[1em] \Rightarrow 12 + \dfrac{11}{6}x \le 5 + 3x \\[1em] \Rightarrow 3x - \dfrac{11}{6}x \ge 12 - 5 \\[1em] \Rightarrow \dfrac{18x - 11x}{6} \ge 7 \\[1em] \Rightarrow \dfrac{7x}{6} \ge 7 \\[1em] \Rightarrow x \ge \dfrac{7 \times 6}{7} \\[1em] \Rightarrow x \ge 6.$

∴ Solution set = {x : x ∈ R and x ≥ 6}.

Given x ∈ {whole numbers}, find the solution set of :

-1 ≤ 3 + 4x < 23

Answer

Given,

-1 ≤ 3 + 4x < 23

Solving L.H.S. of the equation,

⇒ -1 ≤ 3 + 4x

⇒ 4x ≥ -1 - 3

⇒ 4x ≥ -4

⇒ x ≥ -1 ........(i)

Solving R.H.S. of the equation,

⇒ 3 + 4x < 23

⇒ 4x < 23 - 3

⇒ 4x < 20

⇒ x < 5 .........(ii)

From (i) and (ii) we get,

-1 ≤ x < 5

Since, x ∈ {whole numbers},

∴ Solution set = {0, 1, 2, 3, 4}.

Find the set of values of x, satisfying :

7x + 3 ≥ 3x - 5 and $\dfrac{x}{4} - 5 \le \dfrac{5}{4} - x$, where x ∈ N.

Answer

Solving,

⇒ 7x + 3 ≥ 3x - 5

⇒ 7x - 3x ≥ -5 - 3

⇒ 4x ≥ -8

⇒ x ≥ -2 .......(i)

Solving,

$\Rightarrow \dfrac{x}{4} - 5 \le \dfrac{5}{4} - x \\[1em] \Rightarrow \dfrac{x}{4} + x \le \dfrac{5}{4} + 5 \\[1em] \dfrac{x + 4x}{4} \le \dfrac{25}{4} \\[1em] \dfrac{5x}{4} \le \dfrac{25}{4} \\[1em] x \le \dfrac{25}{4} \times \dfrac{4}{5} \\[1em] x \le 5 ........(ii)$

From (i) and (ii) we get,

-2 ≤ x ≤ 5

Since, x ∈ N

∴ Solution set = {1, 2, 3, 4, 5}.

Solve :

(i) $\dfrac{x}{2} + 5 \le \dfrac{x}{3} + 6$, where x is a positive odd integer

(ii) $\dfrac{2x + 3}{3} \ge \dfrac{3x - 1}{4}$, where x is a positive even integer

Answer

(i) Solving,

$\Rightarrow \dfrac{x}{2} + 5 \le \dfrac{x}{3} + 6 \\[1em] \Rightarrow \dfrac{x}{2} - \dfrac{x}{3} \le 6 - 5 \\[1em] \Rightarrow \dfrac{3x - 2x}{6} \le 1 \\[1em] \Rightarrow \dfrac{x}{6} \le 1 \\[1em] \Rightarrow x \le 6.$

Since, x is a positive odd integer

∴ Solution set = {1, 3, 5}.

(ii) Solving,

$\Rightarrow \dfrac{2x + 3}{3} \ge \dfrac{3x - 1}{4} \\[1em] \Rightarrow \dfrac{2x + 3}{3} - \dfrac{3x - 1}{4} \ge 0 \\[1em] \Rightarrow \dfrac{4(2x + 3) - 3(3x - 1)}{12} \ge 0 \\[1em] \Rightarrow 8x + 12 - 9x + 3 \ge 0 \\[1em] \Rightarrow -x + 15 \ge 0 \\[1em] \Rightarrow x \le 15.$

Since, x is a positive even integer

∴ Solution set = {2, 4, 6, 8, 10, 12, 14}.

Solve the inequation :

$-2\dfrac{1}{2} + 2x \le \dfrac{4x}{5} \le \dfrac{4}{3} + 2x$, x ∈ W.

Graph the solution set on the number line.

Answer

Given,

$-2\dfrac{1}{2} + 2x \le \dfrac{4x}{5} \le \dfrac{4}{3} + 2x$

Solving L.H.S. of the equation,

$\Rightarrow -2\dfrac{1}{2} + 2x \le \dfrac{4x}{5} \\[1em] \Rightarrow -\dfrac{5}{2} + 2x \le \dfrac{4x}{5} \\[1em] \Rightarrow 2x - \dfrac{4x}{5} \le \dfrac{5}{2} \\[1em] \Rightarrow \dfrac{10x - 4x}{5} \le \dfrac{5}{2} \\[1em] \Rightarrow \dfrac{6x}{5} \le \dfrac{5}{2} \\[1em] \Rightarrow x \le \dfrac{5}{2} \times \dfrac{5}{6} \\[1em] \Rightarrow x \le \dfrac{25}{12} \\[1em] \Rightarrow x \le 2\dfrac{1}{12} ........(i)$

Solving R.H.S. of the equation,

$\Rightarrow \dfrac{4x}{5} \le \dfrac{4}{3} + 2x \\[1em] \Rightarrow \dfrac{4x}{5} - 2x \le \dfrac{4}{3} \\[1em] \Rightarrow \dfrac{4x - 10x}{5} \le \dfrac{4}{3} \\[1em] \Rightarrow -\dfrac{6x}{5} \le \dfrac{4}{3} \\[1em] \Rightarrow \dfrac{6x}{5} \ge -\dfrac{4}{3} \\[1em] \Rightarrow x \ge -\dfrac{4}{3} \times \dfrac{5}{6} \\[1em] \Rightarrow x \ge -\dfrac{10}{9} \\[1em] \Rightarrow x \ge -1\dfrac{1}{9} .......(ii)$

From (i) and (ii) we get,

$-1\dfrac{1}{9} \le x \le 2\dfrac{1}{12}$

Since, x ∈ W

∴ Solution set = {0, 1, 2}.

Solution on the number line is :

Find three consecutive largest positive integers such that the sum of one-third of first, one-fourth of second and one-fifth of third is at most 20.

Answer

Let three consecutive positive integers be x, x + 1 and x + 2.

Given, sum of one-third of first, one-fourth of second and one-fifth of third is at most 20

$\therefore \dfrac{1}{3}x + \dfrac{1}{4}(x + 1) + \dfrac{1}{5}(x + 2) \le 20 \\[1em] \Rightarrow \dfrac{x}{3} + \dfrac{x + 1}{4} + \dfrac{x + 2}{5} \le 20 \\[1em] \Rightarrow \dfrac{20x + 15(x + 1) + 12(x + 2)}{60} \le 20 \\[1em] \Rightarrow \dfrac{20x + 15x + 15 + 12x + 24}{60} \le 20 \\[1em] \Rightarrow 47x + 39 \le 1200 \\[1em] \Rightarrow 47x \le 1161 \\[1em] \Rightarrow x \le \dfrac{1161}{47} \\[1em] \Rightarrow x \le 24.702$

∴ x = 24, x + 1 = 25, x + 2 = 26.

Hence, three consecutive numbers are 24, 25 and 26.

Solve the following inequation and represent the solution set on the number line :

4x - 19 < $\dfrac{3x}{5} - 2 \le -\dfrac{2}{5} + x$, x ∈ R

Answer

Given,

4x - 19 < $\dfrac{3x}{5} - 2 \le -\dfrac{2}{5} + x$

Solving L.H.S. of the equation,

$\Rightarrow 4x - 19 \lt \dfrac{3x}{5} - 2 \\[1em] \Rightarrow 4x - 19 \lt \dfrac{3x - 10}{5} \\[1em] \Rightarrow 5(4x - 19) \lt 3x - 10 \\[1em] \Rightarrow 20x - 95 \lt 3x - 10 \\[1em] \Rightarrow 20x - 3x \lt 95 - 10 \\[1em] \Rightarrow 17x \lt 85 \\[1em] \Rightarrow x \lt 5 ........(i)$

Solving R.H.S. of the equation,

$\Rightarrow \dfrac{3x}{5} - 2 \le -\dfrac{2}{5} + x \\[1em] \Rightarrow x - \dfrac{3x}{5} \ge -2 + \dfrac{2}{5} \\[1em] \Rightarrow \dfrac{5x - 3x}{5} \ge \dfrac{-10 + 2}{5} \\[1em] \Rightarrow \dfrac{2x}{5} \ge \dfrac{-8}{5} \\[1em] \Rightarrow x \ge -\dfrac{8}{5} \times \dfrac{5}{2} \\[1em] \Rightarrow x \ge -4 ........(ii)$

From (i) and (ii) we get,

-4 ≤ x < 5

∴ Solution set = {x : -4 ≤ x < 5, x ∈ R}.

Solution on the number line is :

Solve the following inequation and write the solution set :

13x - 5 < 15x + 4 < 7x + 12, x ∈ R

Represent the solution on a real number line.

Answer

Given,

13x - 5 < 15x + 4 < 7x + 12

Solving L.H.S. of the inequation

⇒ 13x - 5 < 15x + 4

⇒ 15x - 13x > -5 - 4

⇒ 2x > -9

⇒ x > $-\dfrac{9}{2}$

⇒ x > -4.5 .........(i)

Solving R.H.S. of the inequation

⇒ 15x + 4 < 7x + 12

⇒ 15x - 7x < 12 - 4

⇒ 8x < 8

⇒ x < 1 ........(ii)

From (i) and (ii) we get,

-4.5 < x < 1

∴ Solution set = {x : -4.5 < x < 1, x ∈ R}

Solution on the number line is :

Solve the following inequation and represent the solution set on a number line.

$-8\dfrac{1}{2} \lt -\dfrac{1}{2} - 4x \le 7\dfrac{1}{2}$, x ∈ I

Answer

Given,

$-\dfrac{17}{2} \lt -\dfrac{1}{2} - 4x \le \dfrac{15}{2}$

Solving L.H.S. of the inequation,

$\Rightarrow -\dfrac{17}{2} \lt -\dfrac{1}{2} - 4x \\[1em] \Rightarrow 4x \lt -\dfrac{1}{2} + \dfrac{17}{2} \\[1em] \Rightarrow 4x \lt \dfrac{16}{2} \\[1em] \Rightarrow 4x \lt 8 \\[1em] \Rightarrow x \lt 2 ......(i)$

Solving R.H.S. of the inequation,

$\Rightarrow -\dfrac{1}{2} - 4x \le 7\dfrac{1}{2} \\[1em] \Rightarrow \dfrac{-1 - 8x}{2} \le \dfrac{15}{2} \\[1em] \Rightarrow -8x \le 15 + 1 \\[1em] \Rightarrow 8x \ge -16 \\[1em] \Rightarrow x \ge -2 .......(ii)$

From (i) and (ii) we get,

-2 ≤ x < 2

Since, x ∈ I

∴ Solution set = {-2, -1, 0, 1}.

Solution on the number line is :