Median, Quartiles and Mode

Find the median of each of the following sets of numbers:

(i) 25, 6, 13, 20, 15, 8, 22, 9, 16, 21, 18

(ii) 15, 32, 41, 13, 51, 35, 0, 18, 56, 39, 37

(iii) 40, 31, 25, 36, 27, 38, 28, 35

(iv) 56, 81, 51, 42, 69, 85, 72, 35, 66, 92

(v) 15, 9, 47, 12, 48, 10, 75, 3, 17, 81, 4, 27

Answer

(i) By arranging data in ascending order, we get:

6, 8, 9, 13, 15, 16, 18, 20, 21, 22, 25

Number of observations, n = 11, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{11 + 1}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{12}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 6 \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 16.$

Hence, median = 16.

(ii) By arranging data in ascending order, we get:

0, 13, 15, 18, 32, 35, 37, 39, 41, 51, 56

Number of observations, n = 11, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{11 + 1}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{12}{2} \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 6 \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 35$

Hence, median = 35.

(iii) By arranging data in ascending order, we get:

25, 27, 28, 31, 35, 36, 38, 40

Number of observations, n = 8, which is even.

By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{8}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{8}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{4\text{th} \text{ term} + (4 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{4\text{ th} \text{ term} + 5\text{ th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{31 + 35}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{66}{2} \\[1em] \Rightarrow \text{Median} = 33$

Hence, median = 33.

(iv) By arranging data in ascending order, we get:

35, 42, 51, 56, 66, 69, 72, 81, 85, 92

Number of observations, n = 10, which is even.

By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{10}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{10}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{5\text{th} \text{ term} + (5 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{5\text{th} \text{ term} + 6\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{66 + 69}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{135}{2} \\[1em] \Rightarrow \text{Median} = 67.5$

Hence, median = 67.5.

(v) By arranging data in ascending order, we get:

3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81

Number of observations, n = 12, which is even.

By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{12}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{12}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{6\text{th} \text{ term} + (6 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{6\text{ th} \text{ term} + 7\text{ th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{15 + 17}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{32}{2} \\[1em] \Rightarrow \text{Median} = 16$

Hence, median = 16.

The marks of 15 students in an examination are given below :

17, 35, 21, 17, 19, 25, 29, 23, 24, 31, 40, 19, 22, 20, 26.

Find the median score.

Answer

By arranging data in ascending order, we get:

17, 17, 19, 19, 20, 21, 22, 23, 24, 25, 26, 29, 31, 35, 40

Number of observations, n = 15, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{15 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{16}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 8 \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 23$

Hence, median score = 23.

The heights (in cm) of 9 girls in a class are given below:

148.5, 143.7, 152.1, 150, 149.6, 144.2, 145, 147.3, 146.5

Find the median height.

Answer

By arranging data in ascending order, we get:

143.7, 144.2, 145, 146.5, 147.3, 148.5, 149.6, 150, 152.1

Number of observations, n = 9, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{9 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{10}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 5 \text{ th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 147.3$

Hence, median height = 147.3 cm.

The weights (in kg) of 8 children are given below:

10.6, 12.7, 9.8, 17.2, 13.4, 15, 16.5, 14.3

Find the median weight.

Answer

By arranging data in ascending order, we get:

9.8, 10.6, 12.7, 13.4, 14.3, 15, 16.5, 17.2

Number of observations, n = 8, which is even.

By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{8}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{8}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{4\text{th} \text{ term} + (4 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{4\text{ th} \text{ term} + 5\text{ th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{13.4 + 14.3}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{27.7}{2} \\[1em] \Rightarrow \text{Median} = 13.85$

Hence, median weight = 13.85 kg.

(i) The median of the observations 11, 12, 14, 18, (x + 4), 30, 32, 35, 41 arranged in ascending order is 24. Find the value of x.

(ii) If 10, 13, 15, 18, x + 1, x + 3, 31, 36, 38, 42 are the observations arranged in ascending order with median 28, find the value of x.

Answer

(i) Set of numbers are arranged in ascending order,

11, 12, 14, 18, (x + 4), 30, 32, 35, 41

Given,

Median = 24.

Here,

Number of observations (n) = 9, which is odd.

$\Rightarrow \text{Median} = \dfrac{9 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow 24 = \dfrac{10}{2} \text{th} \text{ observation} \\[1em] \Rightarrow 24 = 5 \text{ th} \text{ observation} \\[1em] \Rightarrow 24 = \text{x} + 4 \\[1em] \Rightarrow \text{x} = 24 - 4 \\[1em] \Rightarrow \text{x} = 20$

Hence, the value of x = 20.

(ii) Set of numbers are arranged in ascending order,

10, 13, 15, 18, x + 1, x + 3, 31, 36, 38, 42

Given,

Median = 28.

Here,

Number of observations (n) = 10, which is even.

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow 28 = \dfrac{\Big(\dfrac{10}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{10}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow 28 = \dfrac{5 \text{th} \text{ term} + (5 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow 28 = \dfrac{5 \text{th} \text{ term} + 6\text{th} \text{ term}}{2} \\[1em] \Rightarrow 28 \times 2 = (\text{x} + 1) + (\text{x} + 3) \\[1em] \Rightarrow 56 = 4 + 2\text{x} \\[1em] \Rightarrow 2\text{x} = 56 - 4 \\[1em] \Rightarrow 2\text{x} = 52 \\[1em] \Rightarrow \text{x} = \dfrac{52}{2} \\[1em] \Rightarrow \text{x} = 26.$

Hence, the value of x = 26.

Calculate the median of the following frequency distribution:

Answer

Cumulative frequency distribution table :

Here number of observations, n = 41, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{41 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{42}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 21 \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \text{Weight of 21 st student}$

From the above table, weight of each student from 20th to 28th are 50.

∴ Weight of 21st student = 50.

Hence, median weight = 50 kg.

Find the median of the following frequency distribution:

Answer

The given varieties are arranged in ascending order.

Cumulative frequency distribution table :

Here number of observations, n = 37, which is odd.

By formula,

$\Rightarrow \text{Median} = \dfrac{37 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{38}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 19 \text{ th} \text{ observation}$

From the above table, variate corresponding to a cumulative frequency from 18th to 21st are 22.

∴ 19th observation = 22.

Hence, median = 22.

50 persons were examined through X-ray and observations were noted as under:

Find :

(i) The mean diameter of heart,

(ii) The median diameter of heart.

Answer

(i) We know that,

$\Rightarrow \text{Mean} = \dfrac{\text{Σfx}}{\text{Σf}} \\[1em] \Rightarrow \text{Mean} = \dfrac{6133}{50} \\[1em] \Rightarrow \text{Mean} = 122.66 \text{ mm}.$

Hence, mean diameter of heart = 122.66 mm.

(ii) Here,

Number of observations (n) = 50, which is even.

By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{50}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{50}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{25 \text{th} \text{ term} + (25 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{25 \text{ th} \text{ term} + 26\text{ th} \text{ term}}{2}$

From table,

Diameter of heart corresponding to 25th term is 122

Diameter of heart corresponding to 26th term is 123

$\Rightarrow \text{Median} = \dfrac{25 \text{th} \text{ term} + 26\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{122 + 123}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{245}{2} \\[1em] \Rightarrow \text{Median} = 122.5 \text{ mm}.$

Hence, median diameter of heart = 122.5 mm.

The marks scored by 15 students in a class test are:

14, 20, 8, 17, 25, 27, 20, 16, 25, 0, 5, 19, 17, 30, 6

Find :

(i) Median

(ii) Lower quartile (Q₁)

(iii) Upper quartile (Q₃)

(iv) Interquartile range

(v) Semi-interquartile range

Answer

By arranging data in ascending order, we get:

0, 5, 6, 8, 14, 16, 17 17, 19, 20, 20, 25, 25, 27, 30

Number of observations, n = 15, which is odd.

(i) By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{15 + 1}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = \dfrac{16}{2} \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 8 \text{th} \text{ observation} \\[1em] \Rightarrow \text{Median} = 17$

Hence, median = 17.

(ii) By formula,

Lower Quartile = $\Big(\dfrac{\text{n} + 1}{4}\Big)$ th term

= $\Big(\dfrac{15 + 1}{4}\Big) = \dfrac{16}{4}$ th term

= 4th term

= 8

Hence, lower quartile (Q₁) = 8.

(iii) By formula,

Upper Quartile (Q₃) = $\Big(\dfrac{3(\text{n} + 1)}{4}\Big)$ th term

= $\Big(\dfrac{3 \times (15 + 1)}{4}\Big)$ th term

= $\Big(\dfrac{3 \times 16}{4}\Big) = \dfrac{48}{4}$ th term

= 12th term

= 25.

Hence, Upper Quartile (Q₃) = 25.

(iv) By formula,

Inter quartile range = Upper quartile - Lower quartile

= 25 - 8

= 17

Hence, the inter-quartile range is 17.

(v) By formula,

Semi-interquartile range = $\dfrac{1}{2}$ × Inter quartile range

= $\dfrac{1}{2} \times 17$

= 8.5

Hence, semi-interquartile range = 8.5.

Find :

(i) Median

(ii) Lower quartile (Q₁)

(iii) Upper quartile (Q₃)

(iv) Interquartile range

(v) Semi-interquartile range for the following series :

5, 23, 9, 16, 0, 14, 19, 8, 2, 26, 13, 18

Answer

By arranging data in ascending order, we get:

0, 2, 5, 8, 9, 13, 14, 16, 18, 19, 23, 26

Number of observations, n = 12, which is even.

(i) By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{12}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{12}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{6 \text{th} \text{ term} + (6 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{6 \text{th} \text{ term} + 7\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{13 + 14}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{27}{2} \\[1em] \Rightarrow \text{Median} = 13.5$

Hence, Median = 13.5.

(ii) By formula,

Lower Quartile = $\Big(\dfrac{\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{12}{4}\Big)$ th term

= 3 rd term

= 5.

Hence, lower quartile (Q₁) = 5.

(iii) By formula,

Upper Quartile (Q₃) = $\Big(\dfrac{3\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{3 \times 12}{4}\Big)$ th term

= $\Big(\dfrac{36}{4}\Big)$ th term

= 9 th term

= 18.

Hence, Upper Quartile (Q₃) = 18.

(iv) By formula,

Inter quartile range = Upper quartile - Lower quartile

= 18 - 5

= 13.

Hence, the inter-quartile range is 13.

(v) By formula,

Semi-interquartile range = $\dfrac{1}{2}$ × Inter quartile range

= $\dfrac{1}{2} \times 13$

= 6.5

Hence, semi-interquartile range = 6.5.

From the following frequency distribution, find:

(i) Median

(ii) Lower quartile

(iii) Upper quartile

(iv) Semi-interquartile range

Answer

The given varieties are arranged in ascending order.

Cumulative frequency distribution table :

Here number of observations, n = 60, which is even.

(i) By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{60}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{60}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{30 \text{th} \text{ term} + (30 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{30 \text{th} \text{ term} + 31\text{th} \text{ term}}{2}$

From table,

30th term is 20

31st term is 22 (All observations from 31st to 46th term = 22)

$\Rightarrow \text{Median} = \dfrac{30 \text{th} \text{ term} + 31 \text{st} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{20 + 22}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{42}{2} \\[1em] \Rightarrow \text{Median} = 21$

Hence, median = 21.

(ii) By formula,

Lower Quartile = $\Big(\dfrac{\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{60}{4}\Big)$ th term

= 15 th term

= 18.

Hence, lower quartile = 18.

(iii) By formula,

Upper Quartile = $\Big(\dfrac{3\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{3 \times 60}{4}\Big)$ th term

= $\Big(\dfrac{180}{4}\Big)$ th term

= 45 th term

= 22

Hence, Upper Quartile = 22.

(iv) By formula,

Semi-interquartile range = $\dfrac{1}{2}$ × (Upper quartile - Lower quartile)

= $\dfrac{1}{2} \times (22 - 18) = \dfrac{1}{2} \times 4$

= 2

Hence, semi-interquartile range = 2.

The heights (in nearest cm) of 63 students of a certain school are given in the following frequency distribution table:

Find :

(i) Median

(ii) Lower quartile (Q₁)

(iii) Upper quartile (Q₃)

(iv) Interquartile range from the above data.

Answer

The given varieties are arranged in ascending order.

Cumulative frequency distribution table :

Here number of observations, n = 63, which is odd.

(i) By formula,

$\Rightarrow \text{Median} = \dfrac{\text{n} + 1}{2} \text{th} \text{observation} \\[1em] \Rightarrow \text{Median} = \dfrac{63 + 1}{2} \text{th} \text{observation} \\[1em] \Rightarrow \text{Median} = \dfrac{64}{2} \text{th} \text{observation} \\[1em] \Rightarrow \text{Median} = 32 \text{th} \text{observation}$

From table,

32 nd term is 153.

Hence, median = 153.

(ii) By formula,

Lower Quartile = $\Big(\dfrac{\text{n} + 1}{4}\Big)$ th term

= $\Big(\dfrac{63 + 1}{4}\Big) = \dfrac{64}{4}$ th term

= 16 th term

From table,

16 th term is 151.

Hence, lower quartile = 151.

(iii) By formula,

Upper Quartile = $\Big(\dfrac{3(\text{n} + 1)}{4}\Big)$ th term

= $\Big(\dfrac{3 \times (63 + 1)}{4}\Big)$ th term

= $\Big(\dfrac{3 \times 64}{4}\Big) = \dfrac{192}{4}$ th term

= 48th term

From table,

48 th term is 154.

Hence, Upper Quartile = 154.

(iv) By formula,

Inter quartile range = Upper quartile - Lower quartile

= 154 - 151

= 3.

Hence, the inter-quartile range is 3.

From the following frequency distribution find :

(i) Median

(ii) Lower quartile (Q₁)

(iii) Upper quartile (Q₃)

(iv) Interquartile range

Answer

The given varieties are arranged in ascending order.

Cumulative frequency distribution table :

Here number of observations, n = 60, which is even.

(i) By formula,

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{\text{n}}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{\text{n}}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{\Big(\dfrac{60}{2}\Big) \text{th} \text{ term} + \Big(\dfrac{60}{2} + 1\Big)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{30 \text{th} \text{ term} + (30 + 1)\text{th} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{30 \text{th} \text{ term} + 31\text{th} \text{ term}}{2}$

From table,

30th term = 20

31st term = 23

$\Rightarrow \text{Median} = \dfrac{30 \text{ th} \text{ term} + 31 \text { st} \text{ term}}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{20 + 23}{2} \\[1em] \Rightarrow \text{Median} = \dfrac{43}{2} \\[1em] \Rightarrow \text{Median} = 21.5$

Hence, median = 21.5.

(ii) By formula,

Lower Quartile = $\Big(\dfrac{\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{60}{4}\Big)$ th term

= 15 th term

= 18.

Hence, lower quartile = 18.

(iii) By formula,

Upper Quartile = $\Big(\dfrac{3\text{n}}{4}\Big)$ th term

= $\Big(\dfrac{3 \times 60}{4}\Big)$ th term

= $\Big(\dfrac{180}{4}\Big)$ th term

= 45 th term

= 28.

Hence, Upper Quartile = 28.

(iv) By formula,

Interquartile range = Upper quartile - Lower quartile

= 28 - 18

= 10

Hence, interquartile range = 10.

The following table shows the weights (in gm) of a sample of 100 apples, taken from a large consignment:

(i) Construct the cumulative frequency table

(ii) Draw the cumulative frequency curve on a graph paper and from it, determine the median weight of the apples.

Answer

(i) The cumulative frequency distribution table is as follows:

(ii) Steps of construction :

1. Take 1 cm along x- axis = 10 grams

2. Take 1 cm along y- axis = 10 units

3. A kink is drawn near x-axis to show that the scale starts from 50 and not zero. Plot the point (50, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (60, 8), (70, 18), (80, 30), (90, 46), (100, 64), (110, 78), (120, 90), (130, 100)

5. Joint the points by a free hand curve.

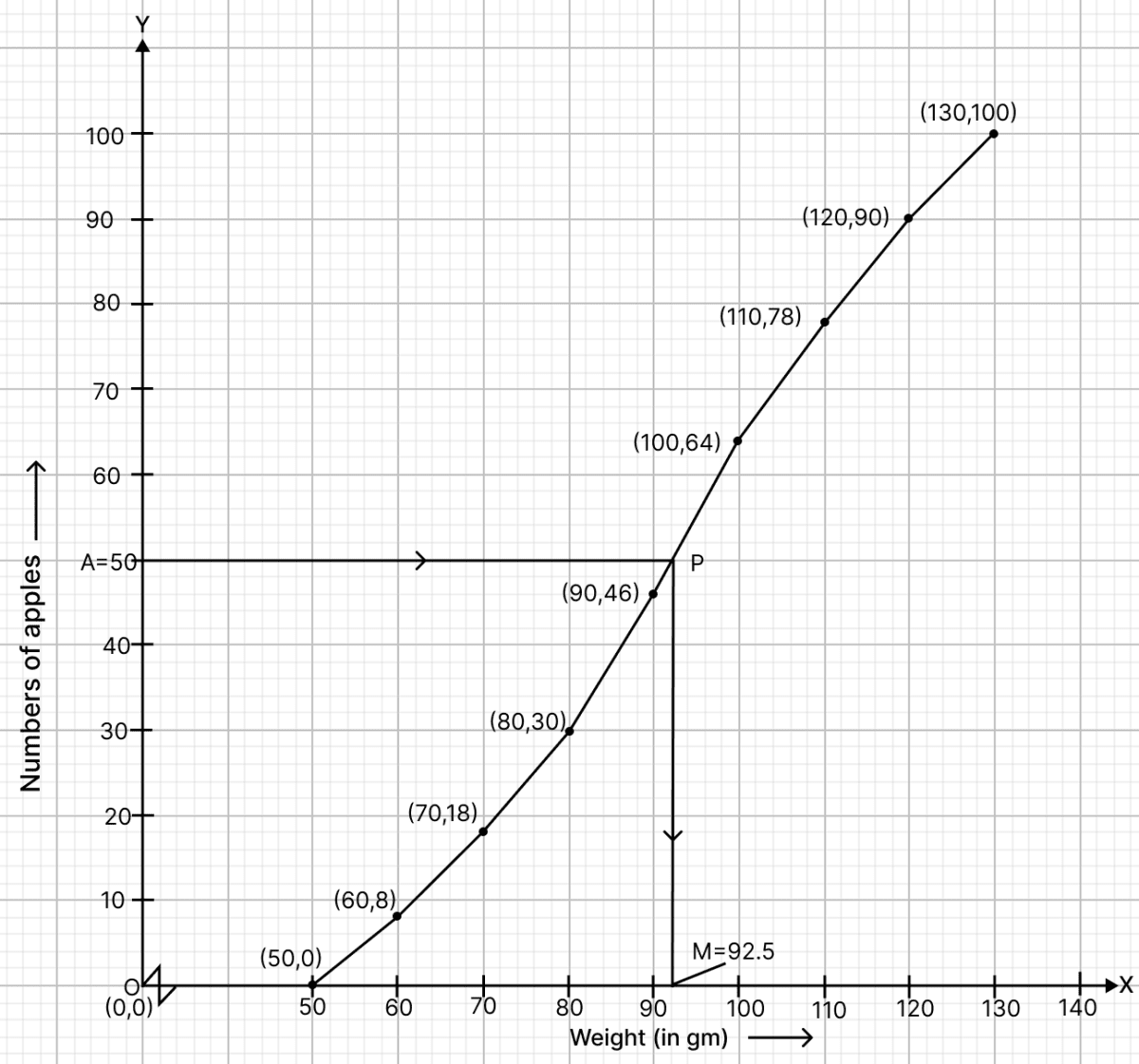
Here, n (no, of students) = 100.

To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{100}{2}$ = 50.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 92.5.

Hence, the median weight is 92.5 gm.

Marks obtained by 200 students in an examination are given below:

Draw an ogive for the given distribution taking 1 cm = 10 marks on one axis and 2 cm = 20 students on other axis.

Using the graph, determine :

(i) The median marks

(ii) The number of students who failed, if minimum marks required to pass is 40.

(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.

Answer

The cumulative frequency distribution table is as follows:

Steps of construction :

1. Take 1 cm along x- axis = 10 marks

2. Take 2 cm along y- axis = 20 students

3. Plot the point (0, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (10, 5), (20, 16), (30, 26), (40, 46), (50, 74), (60, 111), (70, 151), (80, 180), (90, 194), (100, 200).

5. Joint the points by a free hand curve.

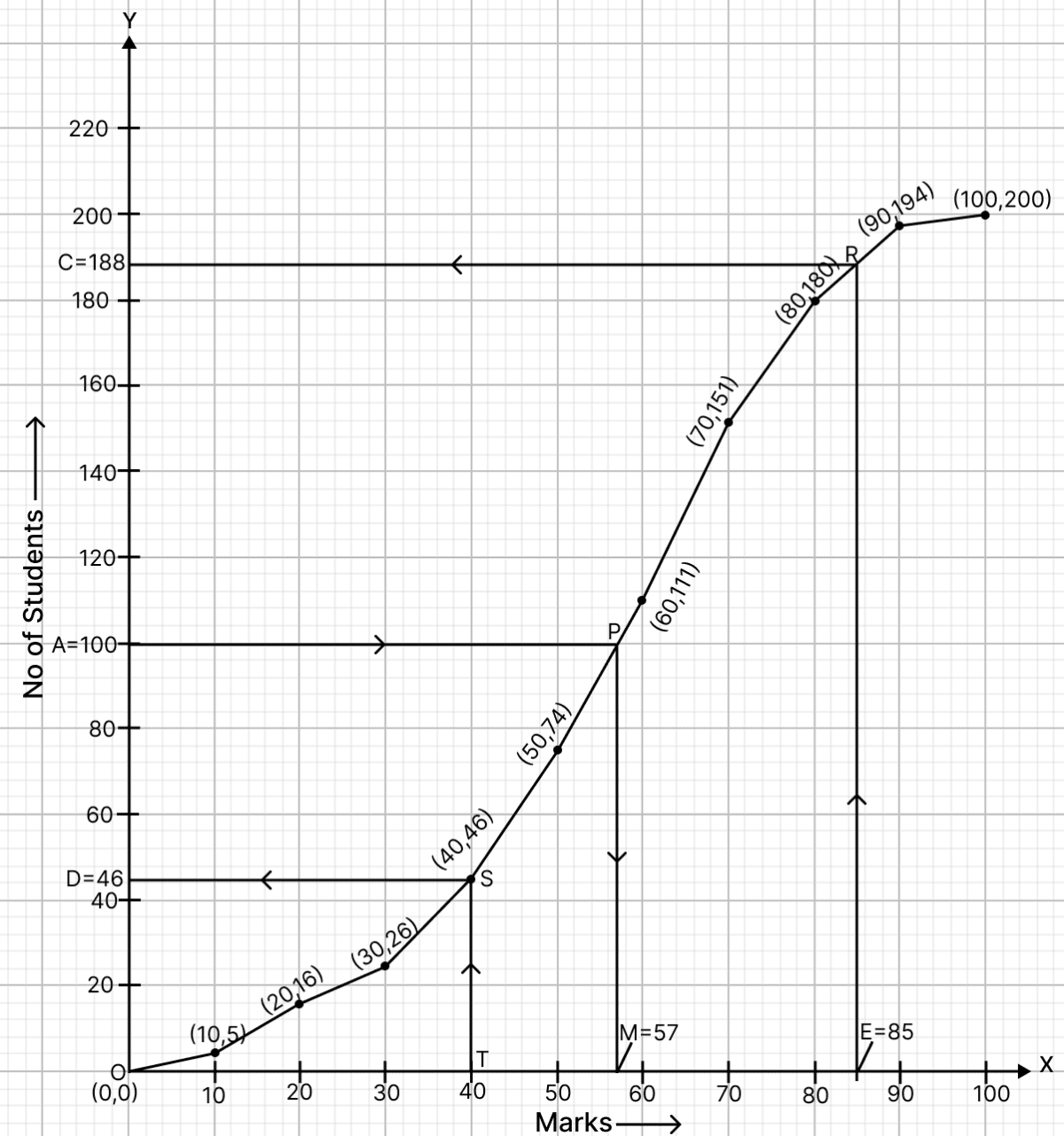
(i) Here, n (no, of students) = 200.

To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{200}{2}$ = 100.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 57.

Hence, the median marks is 57.

(ii) Minimum passing marks = 40

Let T be the point on x-axis representing marks = 40

Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at D.

D = 46

No. of students who scored less than 40 marks = 46

Hence, the no. of students who failed if the minimum marks required to pass is 40 = 46.

(iii) Total marks = 100.

Given, scoring 85 and more marks is considered as grade one.

Let E = 85.

Through E draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C.

C = 188.

Hence, 188 students score less than or equal to 85, so, students scoring more than 85 = 200 - 188 = 12.

Hence, the number of students who scored more than 85 marks in the examination is 12.

Marks obtained by 200 students in an examination are given below:

Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on other axis. From the graph, find:

(i) the median

(ii) the upper-quartile

(iii) number of students scoring more than 65 marks

(iv) if 10 students qualify for merit-scholarship, find the minimum marks required to qualify.

Answer

Cumulative frequency distribution table :

Here, n = 200, which is even.

Steps of construction:

1. Take 1 cm along x-axis = 10 marks

2. Take 2 cm along y-axis = 20 students

3. Plot the point (0, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (10, 5), (20, 15), (30, 29), (40, 50), (50, 75), (60, 109), (70, 145), (80, 172), (90, 188), (100, 200).

5. Joint the points by a free hand curve.

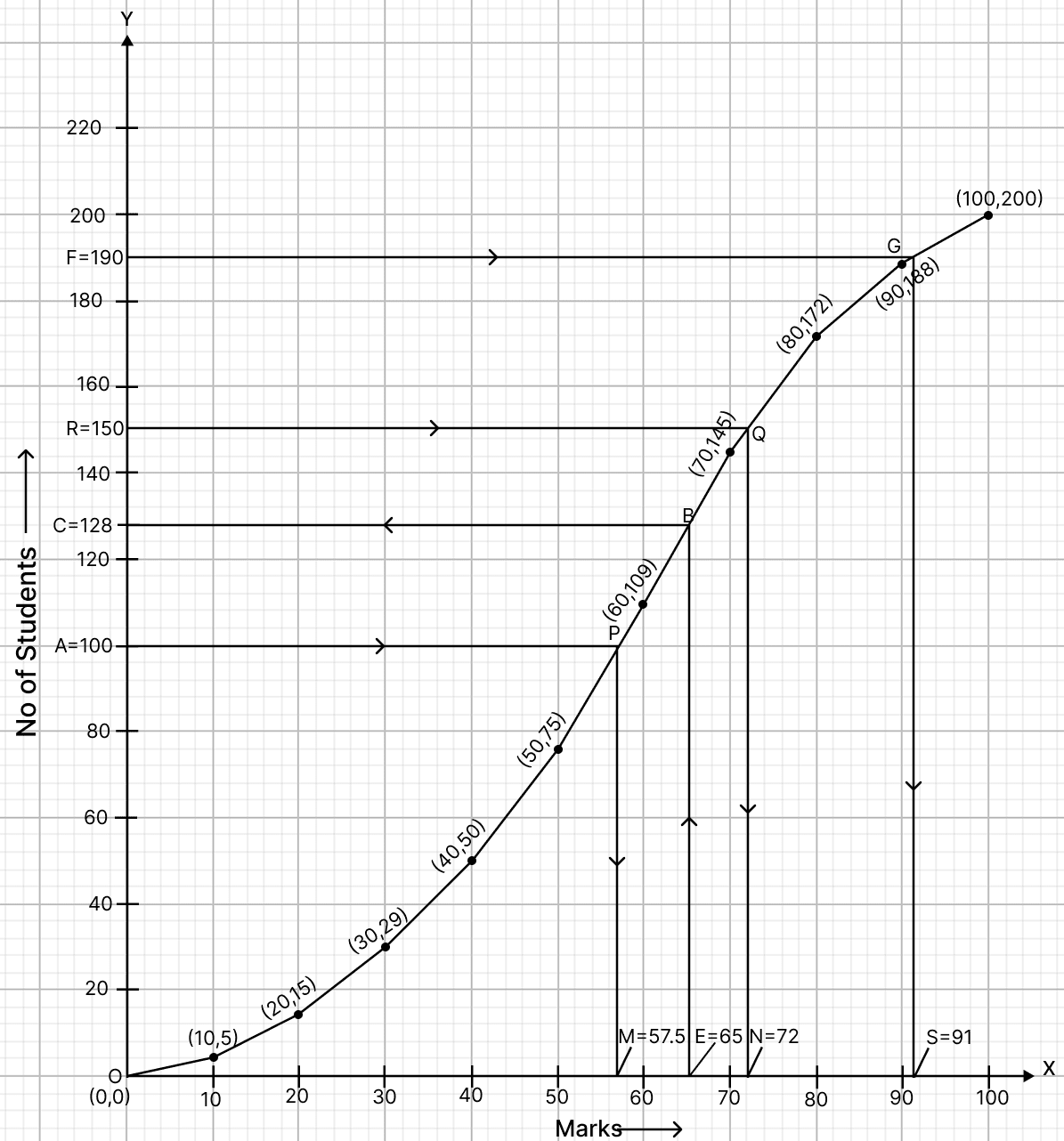
(i) To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{200}{2}$ = 100.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 57.5.

Hence, the median is 57.5.

(ii) By formula,

$\text{Upper quartile} = \Big(\dfrac{3\text{n}}{4}\Big)^ \text{th}\text{ term} \\[1em] \Rightarrow \text{Upper quartile} = \Big(\dfrac{(3 \times 200)}{4}\Big)^\text{th}\text{ term} \\[1em] \Rightarrow \text{Upper quartile} = \dfrac{600}{4}^\text{th}\text{ term} \\[1em] \Rightarrow \text{Upper quartile} = 150^\text{ th}\text{ term} \\[1em]$

Draw a line parallel to x-axis from point R (Number of students) = 150, touching the graph at point Q. From point Q draw a line parallel to y-axis touching x-axis at point N.

From graph,

N = 72

Hence, the upper quartile is 72.

(iii) Total marks = 100.

Let E be the point on x-axis representing marks = 65.

Through E draw a vertical line to meet the ogive at B. Through B, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 128.

Hence, 128 students score less than or equal to 65, so, students scoring more than 65 = 200 - 128 = 72.

Hence, the number of students who scored more than 65 marks is 72.

(iv) Given, 10 students qualify for merit-scholarship. This corresponds to 190th student. Since, 200 - 10 = 190

Draw a line parallel to x-axis from point F = 190, touching the graph at point G. From point G draw a line parallel to y-axis touching x-axis at point S.

From graph,

S = 91

Hence, the minimum marks required to qualify is 91.

The table below shows the distribution of the scores obtained by 120 shooters in shooting competition. Using a graph sheet, draw an ogive for the distribution.

Use your ogive to estimate :

(i) the median

(ii) the inter-quartile range

(iii) the number of shooters who obtained more than 75% score.

Answer

Cumulative frequency distribution table :

Here, n = 120, which is even.

(i) Steps of construction:

1. Take 1 cm along x-axis = 10 scores

2. Take 2 cm along y-axis = 20 shooters

3. Plot the point (0, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96), (70, 107), (80, 113), (90, 117), (100, 120)

5. Joint the points by a free hand curve.

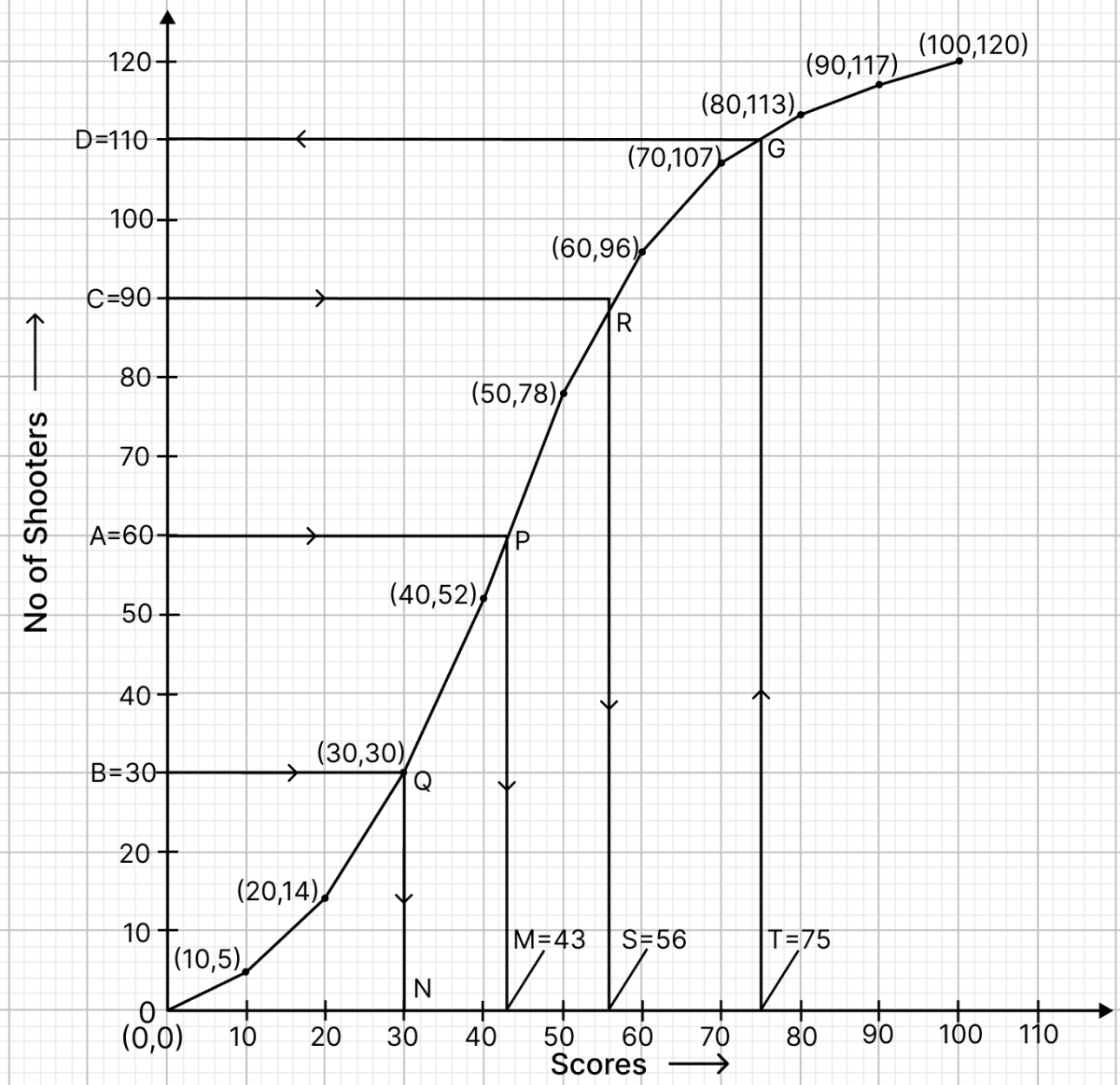
To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{120}{2}$ = 60.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 43.

Hence, the median is 43.

(ii) To find lower quartile:

Let B be the point on y-axis representing frequency = $\dfrac{\text{n}}{4} = \dfrac{120}{4}$ = 30.

Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 30.

To find upper quartile:

Let C be the point on y-axis representing frequency = $\dfrac{3\text{n}}{4} = \dfrac{3 \times 120}{4} = \dfrac{360}{4}$ = 90.

Through C, draw a horizontal line to meet the ogive at R. Through R, draw a vertical line to meet the x-axis at S. The abscissa of the point S represents 56.

Inter-quartile range = Upper quartile - Lower quartile = 56 - 30 = 26

Hence, the inter quartile range is = 26.

(iii) Total score = 100

So, more than 75% score mean more than 75 score.

Let T be the point on x-axis representing scores = 75

Through T, draw a vertical line to meet the ogive at G. Through G, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 110

Shooters who have scored less than 75% = 110

So, students scoring more than 75% = Total students - Students who have scored less = 120 - 110 = 10

Hence, there are 10 number of shooters who obtained more than 75% score.

The daily wages of 80 workers in a project are given below:

Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate:

(i) the median wage of the workers.

(ii) the lower quartile wage of the workers.

(iii) the number of workers who earn more than ₹ 625 daily.

Answer

Cumulative frequency distribution table :

Here, n = 80, which is even.

Steps of construction:

1. Take 2 cm along x-axis = ₹ 50

2. Take 2 cm along y-axis = 10 workers

3. Since, scale on x-axis starts at 400, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 400.

4. Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75), (750, 80) representing upper class limits and the respective cumulative frequencies. Also plot the point representing lower limit of the first class i.e, 400 - 450.

5. Joint the points by a free hand curve.

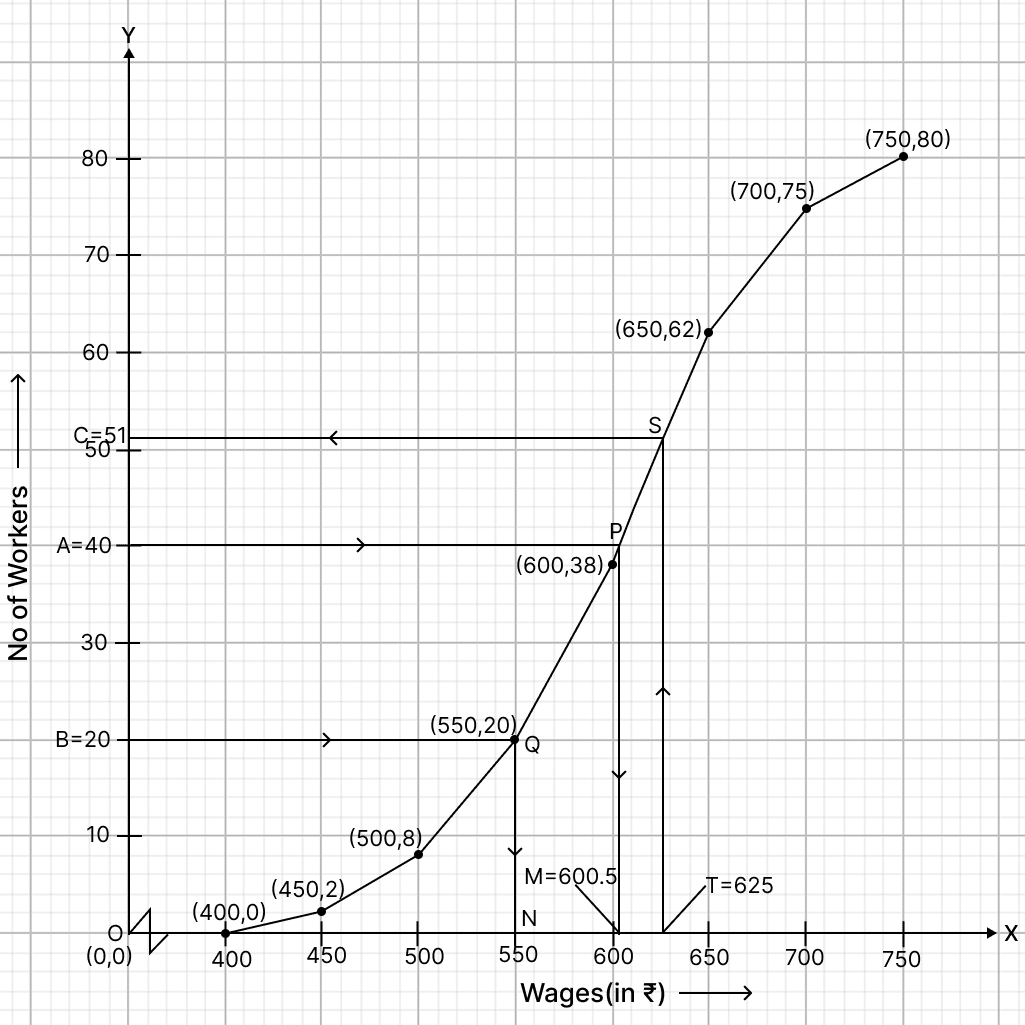
(i) Here, n = 80

To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{80}{2}$ = 40.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 600.5.

Hence, the median is ₹ 600.5.

(ii) To find lower quartile:

Let B be the point on y-axis representing frequency = $\dfrac{\text{n}}{4} = \dfrac{80}{4}$ = 20.

Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 550.

Hence, lower quartile wage = ₹ 550.

(iii) Let T be the point on x-axis representing wage = ₹ 625.

Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at C. The ordinate of the point C. The ordinate of point C represents 51.

Workers who earn less than ₹ 625 = 51.

So, workers earning more than ₹ 625 = Total workers - workers who earn less than ₹ 625 = 80 - 51 = 29.

Hence, there are 29 workers earning more than ₹ 625 daily.

Using a graph paper, draw an ogive for the following distribution which shows a record of the weight in kilograms of 200 students.

Use your ogive to estimate the following :

(i) the percentage of students weighing 55 kg or more

(ii) the weight above which the heaviest 30% of the students fall

(iii) the number of students who are (a) under weight and (b) Over-weight, if 55.70 kg is considered as standard weight.

Answer

Cumulative frequency distribution table :

Here, n = 200, which is even.

Steps of construction:

1. Take 2 cm along x-axis = 5 kg

2. Take 2 cm along y-axis = 20 units.

3. Since, scale on x-axis starts at 40, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 40.

4. Plot the point (40, 0) as ogive starts from x-axis representing lower limit of first class.

5. Plot the points (45, 5), (50, 22), (55, 44), (60, 89), (65, 140), (70, 171), (75, 191) and (80, 200).

6. Join the points by a free hand curve.

7. Draw a line parallel to y-axis from point J(weight) = 55, touching the graph at point Q. From point Q draw a line parallel to x-axis touching y-axis at point K.

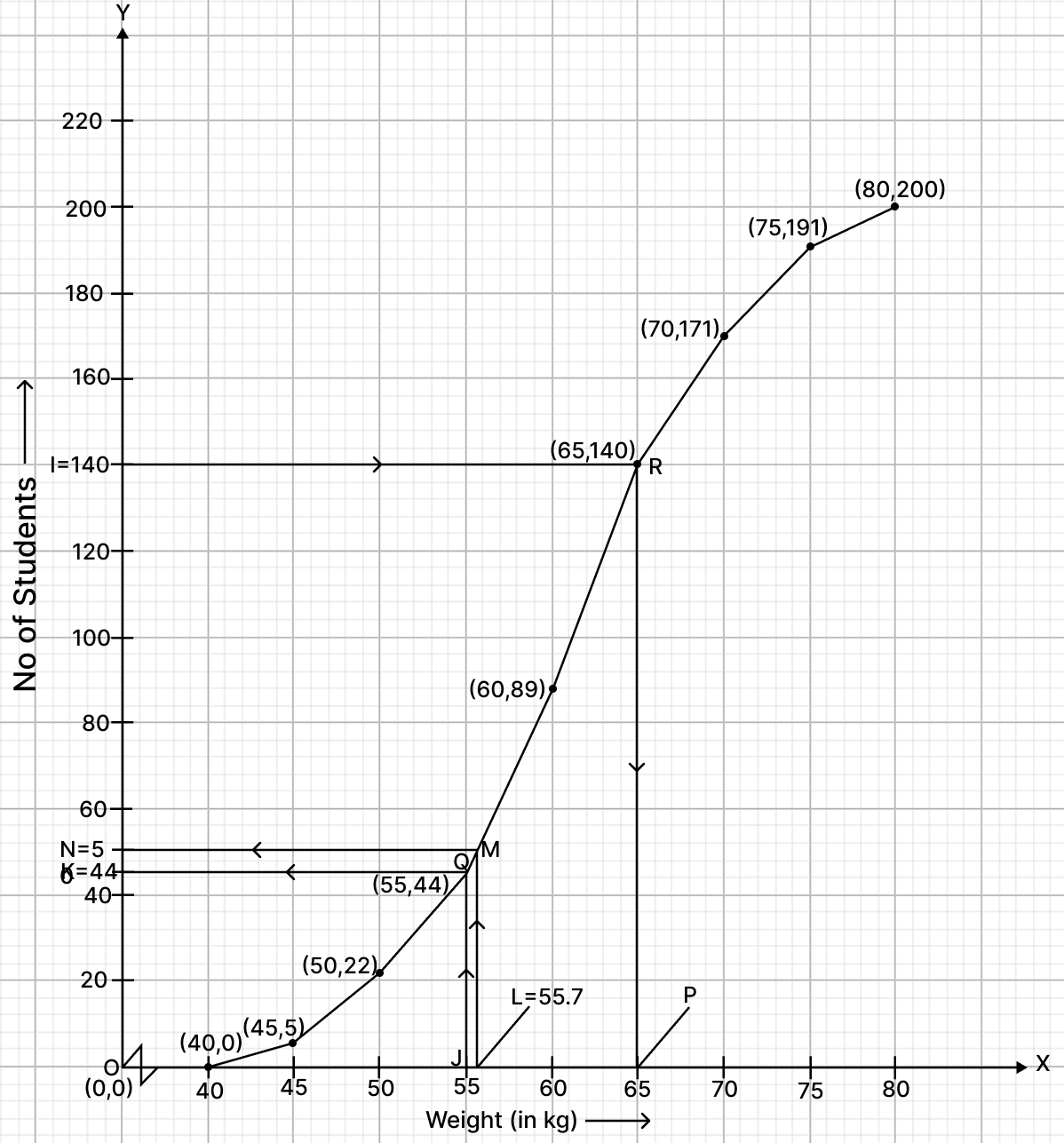
From graph, K = 44.

Hence, 44 students weight 55 kg or less.

Students weighing more than 55 kg = 200 - 44 = 156

Percentage of students weighing more than 55 kg = $\dfrac{156}{200} \times 100$ = 78%

Hence, percentage of students weighing more than 55 kg = 78%.

(ii) 30% of students = $\dfrac{30}{100} \times 200$ = 60.

Total students = 200

No. of students not in heaviest 30% = 200 - 60 = 140.

Draw a line parallel to x-axis from point I (no. of students) = 140, touching the graph at point R. From point R draw a line parallel to y-axis touching x-axis at point P.

From graph, P = 65

Hence, above 65 kg the heaviest 30% of the students fall.

(iii) Draw a line parallel to y-axis from point L (weight) = 55.70 kg, touching the graph at point M. From point M draw a line parallel to x-axis touching y-axis at point N.

(a) From graph,

N = 50.

∴ 50 students have weight less than 55.70 kg

Hence, 50 students are underweight.

(b) Since, 50 students have weight less than 55.70 kg

∴ 150 (200 - 50) students have weight more than 55.70 kg.

Hence, 150 students are overweight.

Using a graph paper, draw an ogive for the distribution which shows the marks obtained on the General knowledge paper by 100 students.

Use the ogive to estimate:

(i) the median

(ii) the number of students whose score is above 65.

Answer

Cumulative frequency distribution table :

Here, n = 100, which is even.

(i) Steps of construction:

1. Take 1 cm along x-axis = 10 marks

2. Take 2 cm along y-axis = 20 students

3. Plot the point (0, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (10, 5), (20, 15), (30, 35), (40, 60), (50, 75), (60, 87), (70, 96), (80, 100).

5. Joint the points by a free hand curve.

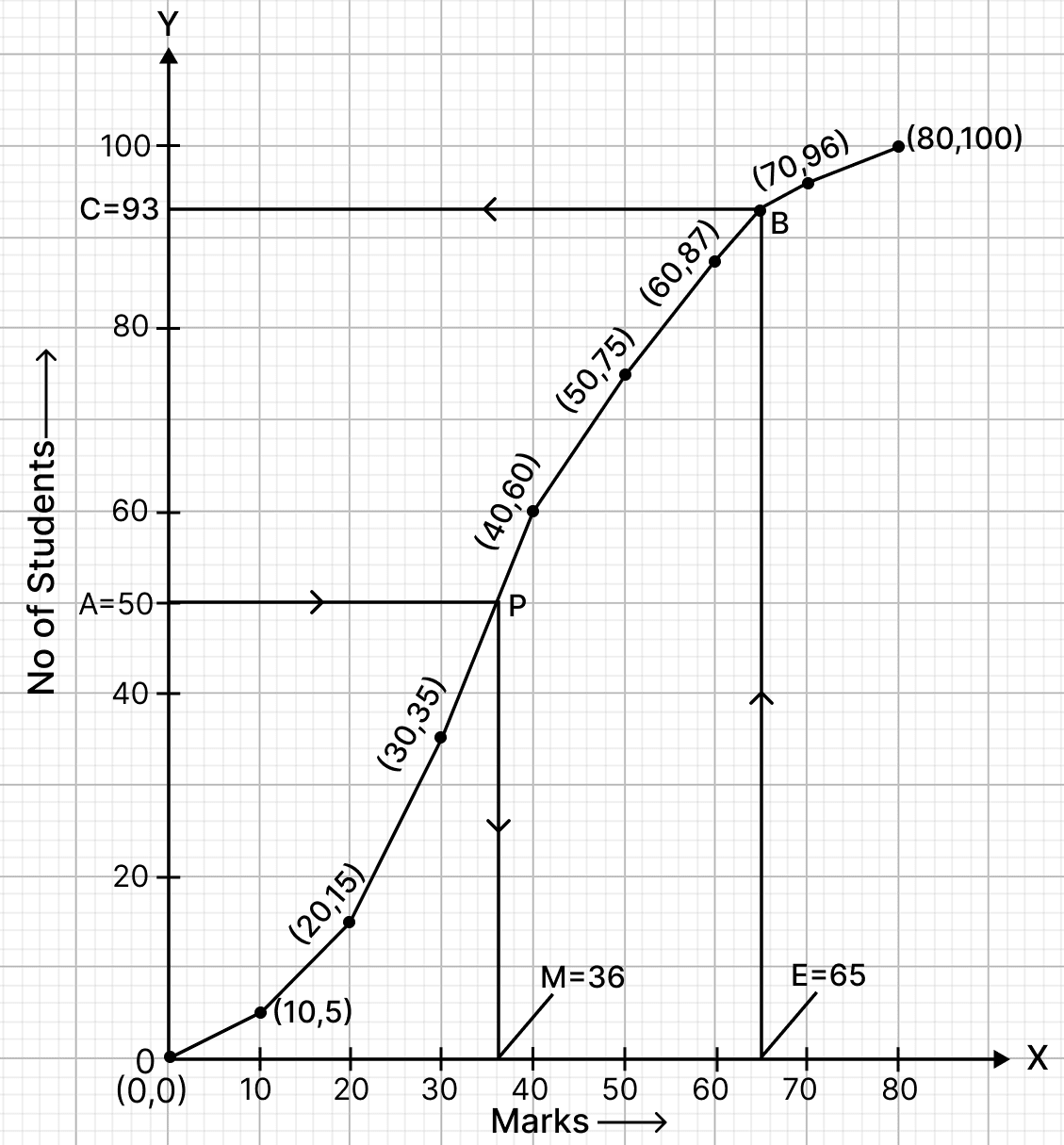
To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{100}{2}$ = 50.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 36.

Hence, the median is 36.

(ii) Total marks = 100.

Let E be the point on x-axis representing marks = 65.

Through E draw a vertical line to meet the ogive at B. Through B, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 93.

Hence, 93 students score less than or equal to 65, so, students scoring more than 65 = 100 - 93 = 7.

Hence, the number of students who scored more than 65 marks is 7.

The table shows the distribution of the scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution (take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis.)

Use your graph to estimate the following:

(i) the median

(ii) the inter-quartile range

(iii) the number of shooters who obtained a score of more than 85%

Answer

Cumulative frequency distribution table :

Here, n = 160, which is even.

(i) Steps of construction:

1. Take 1 cm along x-axis = 10 scores

2. Take 2 cm along y-axis = 20 shooters

3. Plot the point (0, 0) as ogive starts from x- axis representing lower limit of first class.

4. Plot the points (10, 9), (20, 22), (30, 42), (40, 68), (50, 98), (60, 120), (70, 135), (80, 145), (90, 153), (100, 160)

5. Joint the points by a free hand curve.

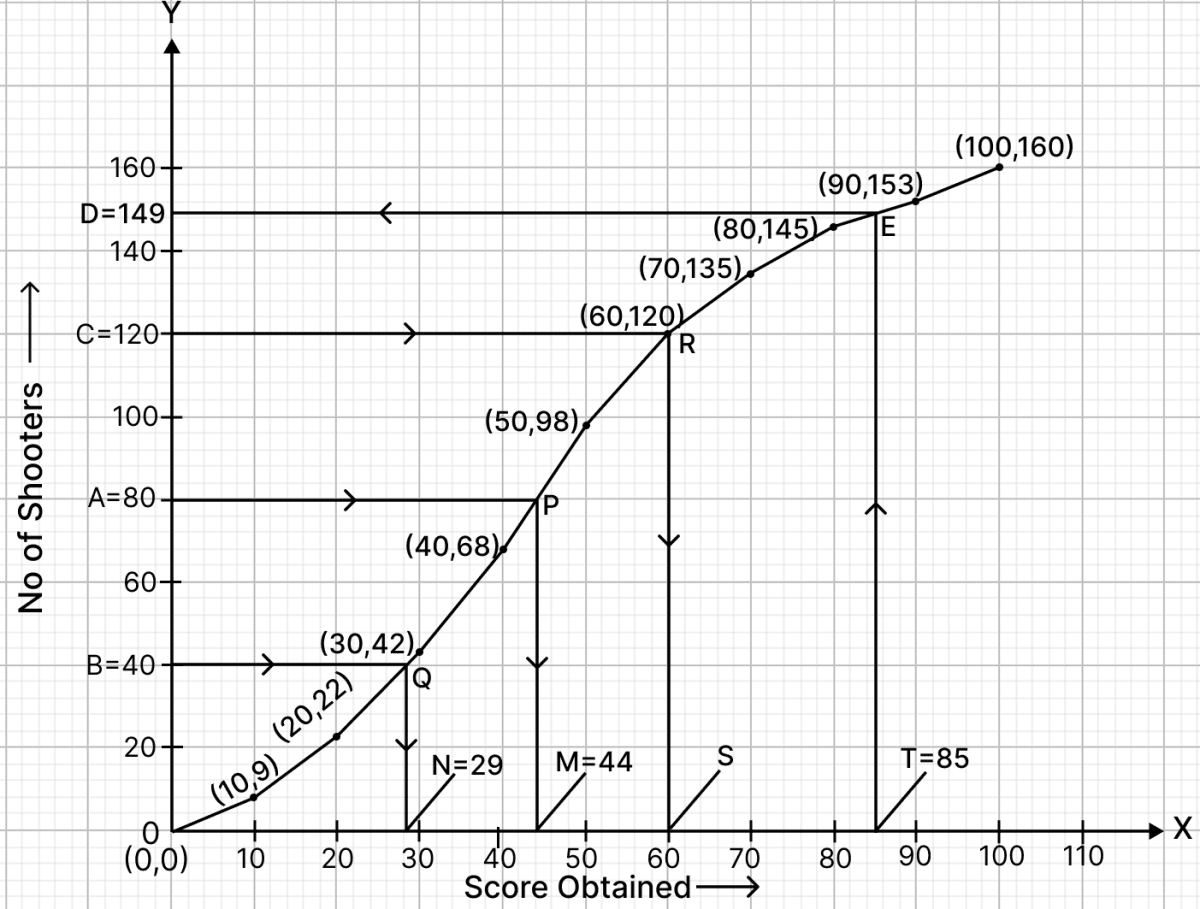
To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{160}{2}$ = 80.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the points M represents 44.

Hence, the median score is 44.

(ii) To find lower quartile:

Let B be the point on y-axis representing frequency = $\dfrac{\text{n}}{4} = \dfrac{160}{4}$ = 40.

Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 29.

To find upper quartile:

Let C be the point on y-axis representing frequency = $\dfrac{3\text{n}}{4} = \dfrac{3 \times 160}{4} = \dfrac{480}{4}$ = 120.

Through C, draw a horizontal line to meet the ogive at R. Through R, draw a vertical line to meet the x-axis at S. The abscissa of the point S represents 60.

Inter-quartile range = Upper quartile - Lower quartile = 60 - 29 = 31.

Hence, the inter quartile range is = 31.

(iii) Total score = 100

So, more than 85% score mean more than 85 score.

Let T be the point on x-axis representing scores = 85

Through T, draw a vertical line to meet the ogive at E. Through E, draw a horizontal line to meet the y-axis at D. The ordinate of the point D represents 149.

Shooters who have scored less than 85% = 149

So, students scoring more than 85% = Total students - Students who have scored less = 160 - 149 = 11.

Hence, there are 11 number of shooters who obtained more than 85% score.

A survey regarding height (in cm) of 60 boys belonging to class 10 of a school was conducted. The following data was recorded:

Taking 2 cm = height of 10 cm along one axis and 2 cm = 10 boys along the other axis, draw an ogive of the above distribution. Use the graph to estimate the following :

(i) the median

(ii) the lower quartile

(iii) if above 158 cm is considered as the tall boys of the class, find the number of boys in the class who are tall.

Answer

The cumulative frequency table for the given continuous distribution is :

1. Take 2 cm along x-axis = 5 cm (height)

2. Take 2 cm along y-axis = 10 (No. of boys)

3. Since, scale on x-axis starts at 135, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 135.

4. Plot the points (140, 4), (145, 12), (150, 32), (155, 46), (160, 53), (165, 59) and (170, 60) representing upper class limits and the respective cumulative frequencies.

Also plot the point (135, 0) representing lower limit of the first class i.e. 135 - 140.

5. Join these points by a freehand drawing.

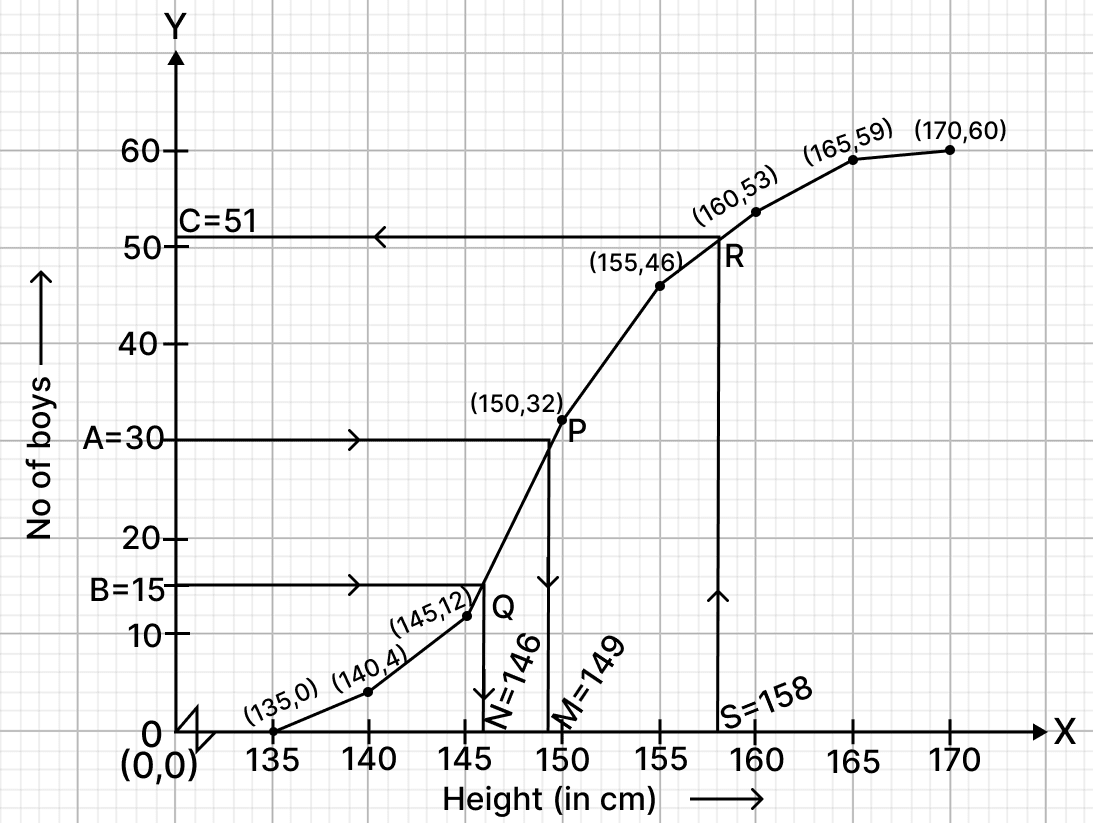
The required ogive is shown in figure above.

(i) Here, n (no. of students) = 60.

To find the median :

Let A be the point on y-axis representing frequency = $\dfrac{\text{n}}{2} = \dfrac{60}{2}$ = 30.

Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 149.

Hence, the median height = 149 cm.

(ii) To find lower quartile :

Let B be the point on y-axis representing frequency = $\dfrac{\text{n}}{4} = \dfrac{60}{4}$ = 15.

Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 146.

Hence, lower quartile = 146 cm.

(iii) Let S be the point on x-axis representing height = 158 cm.

Through S, draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 51.

No. of boys shorter than 158 cm = 51

So, no. of boys taller than 158 cm = Total boys - boys shorter than 158 cm = 60 - 51 = 9.

Hence, there are 9 tall boys in the class.

40 students enter for a game of shot put competition. The distance thrown (in metres) is recorded below.

Use a graph paper to draw an ogive for the above distribution.

Use a scale of 2 cm = 1 m on one axis and 2 cm = 5 students on the other axis. Hence using your graph, find

(i) the median

(ii) Upper quartile

(iii) Number of students who cover a distance which is above 16 $\dfrac{1}{2}$ m.

Answer

Cumulative frequency distribution table :

Steps of construction:

1. Since, the scale on x-axis starts at 12, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 12.

2. Take 2 cm along x-axis = 1 m.

3. Take 2 cm along y-axis = 5 students.

4. Plot the point (12, 0) as ogive starts from x-axis representing lower limit of first class.

5. Plot the points (13, 3), (14, 12), (15, 24), (16, 33), (17, 37), (18, 39) and (19, 40).

6. Join the points by a free hand curve.

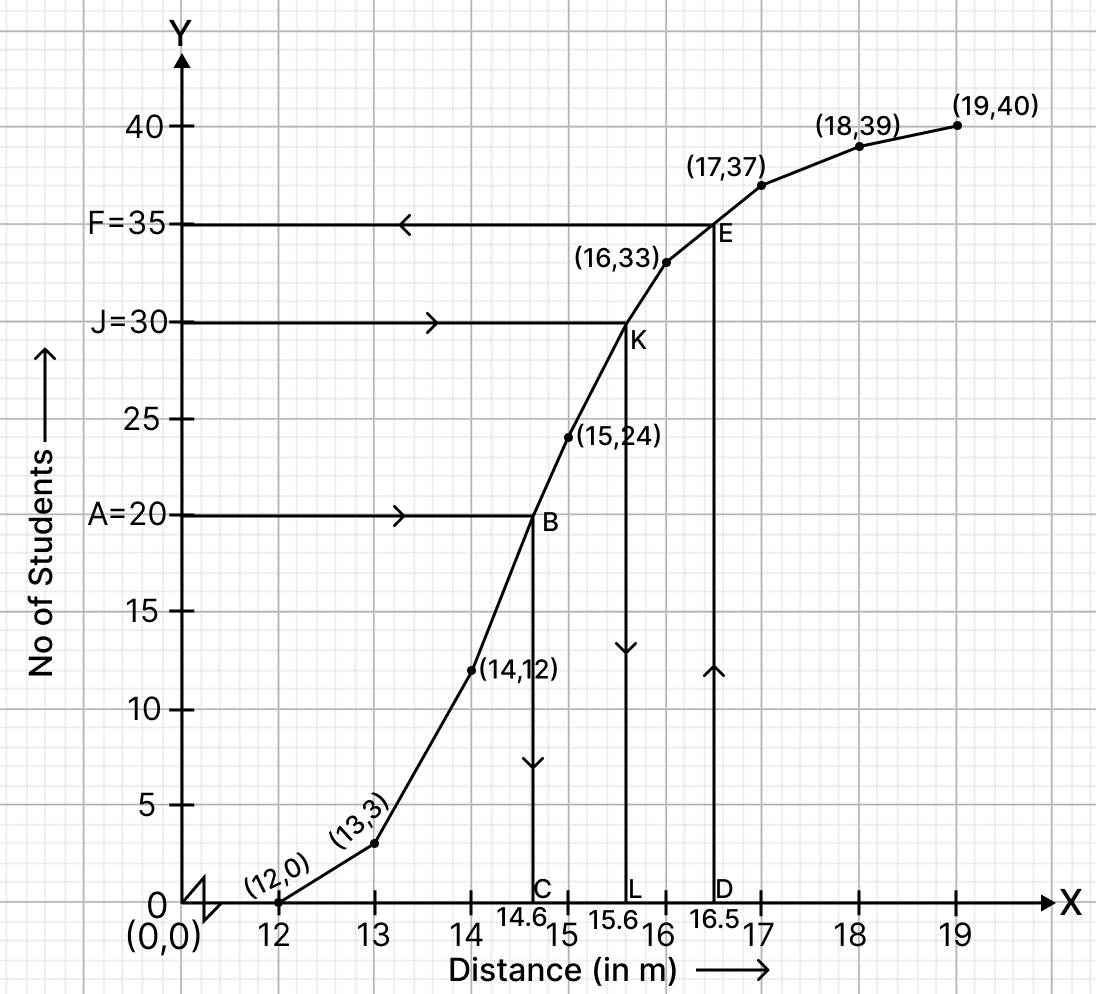
(i) The total number of students is N = 40. The median position is found at $\dfrac{\text{N}}{2} = \dfrac{40}{2}$ = 20.

Draw a line parallel to x-axis from point A (number of students) = 20, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.

From graph, C = 14.6

Hence, the median = 14.6 m.

(ii) Here, n = 40, which is even.

By formula,

Upper quartile = $\dfrac{3\text{N}}{4} = \dfrac{3 \times 40}{4} = \dfrac{120}{4}$ = 30.

Draw a line parallel to x-axis from point J (number of students) = 30, touching the graph at point K. From point K draw a line parallel to y-axis touching x-axis at point L.

From graph, L = 15.6

Hence, the upper quartile = 15.6 m.

(iii) Draw a line parallel to y-axis from point D (Distance) = $16\dfrac{1}{2}$ m = 16.5 m, touching the graph at point E. From point E draw a line parallel to x-axis touching y-axis at point F.

From graph, F = 35.

It means there are 35 students who cover a distance either less or equal to $16\dfrac{1}{2}$ m.

Number of student who cover a distance which is above $16\dfrac{1}{2}$ m = 40 - 35 = 5.

Hence, number of students who cover a distance above $16\dfrac{1}{2}$ m = 5.

Use graph paper to answer this question:

During a medical checkup of 60 students in a school, weights were recorded as follows:

Taking 2 cm = 2 kg along one axis and 2 cm = 10 students along the other axis, draw an ogive. Use your graph to find the:

(i) Median

(ii) Upper quartile

(iii) Number of students whose weight is above 37 kg

Answer

Cumulative frequency distribution table :

Here, n = 60, which is even.

(a) Median = $\dfrac{\text{n}}{2} \text{ th term} = \dfrac{60}{2}$ = 30th term.

Steps of construction :

1. Take 2 cm = 2 kg on x-axis.

2. Take 2 cm = 10 students on y-axis.

3. Since, x axis starts at 28 hence, a kink is drawn at the starting of x-axis. Plot the point (28, 0) as ogive starts on x-axis representing lower limit of first class.

4. Plot the points (30, 2), (32, 6), (34, 16), (36, 29), (38, 44), (40, 53), (42, 58) and (44, 60).

5. Join the points by a free-hand curve.

6. Draw a line parallel to x-axis from point A (no. of students) = 30, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.

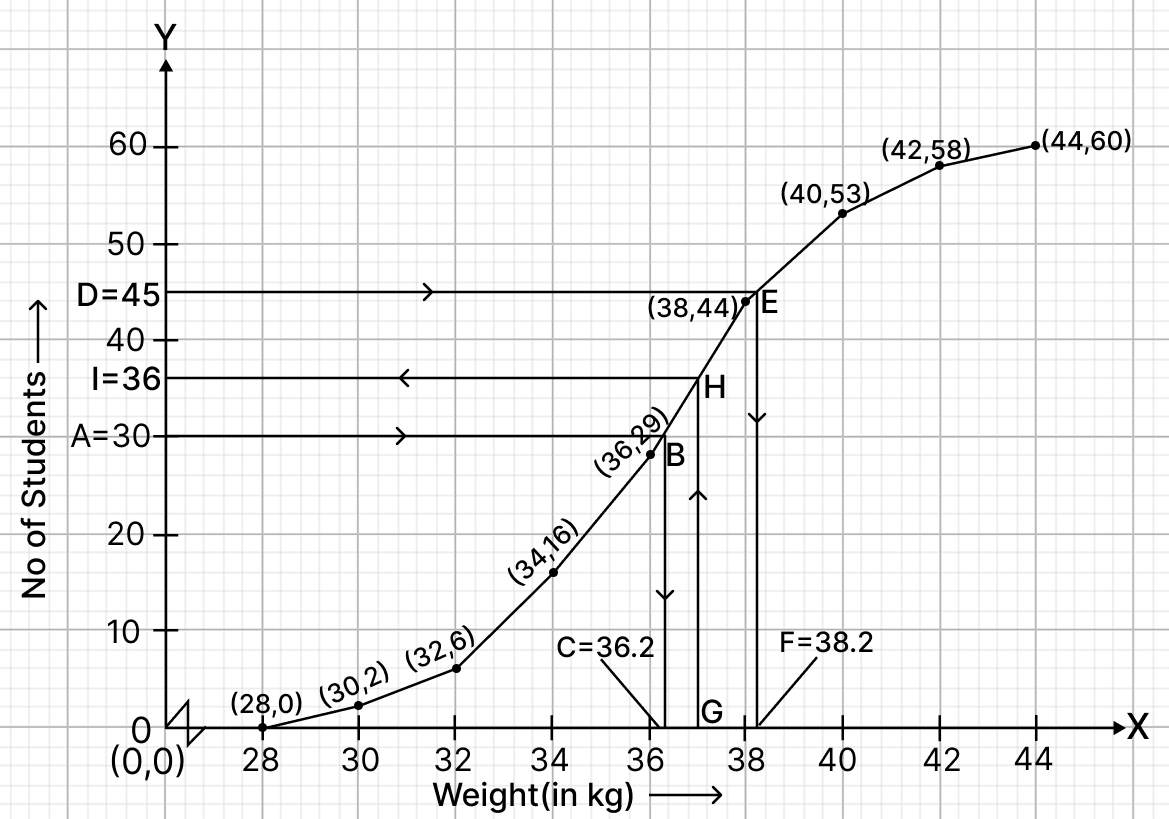
From graph, C = 36.2

Hence, median = 36.2 kg

(ii) Here, n = 60, which is even.

By formula,

Upper quartile = $\dfrac{3\text{n}}{4} = \dfrac{3 \times 60}{4} = \dfrac{180}{4}$ = 45 th term.

Draw a line parallel to x-axis from point D (no. of students) = 45, touching the graph at point E. From point E draw a line parallel to y-axis touching x-axis at point F.

From graph, F = 38.2 kg

Hence, upper quartile = 38.2 kg.

(iii) Draw a line parallel to y-axis from point G (weight) = 37 kg, touching the graph at point H. From point H draw a line parallel to x-axis touching y-axis at point I.

From graph, I = 36.

∴ 36 students have weight less than or equal to 36 kg.

No. of students whose weight is more than 36 kg = 60 - 36 = 24.

Hence, no. of students whose weight is more than 36 kg = 24.

Calculate the mean, median and mode of the following numbers:

(i) 17, 19, 11, 23, 19

(ii) 7, 9, 8, 11, 8, 12, 8, 9

(iii) 2, 1, 0, 3, 1, 2, 3, 4, 3, 5

(iv) 8, 10, 7, 6, 10, 11, 6, 13, 10

Answer

(i) Arranging given observations in ascending order:

11, 17, 19, 19, 23

Sum of observations = 17 + 19 + 11 + 23 + 19 = 89.

By formula,

Mean = $\dfrac{\text{Sum of observation}}{\text{No. of observation}} = \dfrac{89}{5}$ = 17.8

Here n = 5, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{5 + 1}{2} \text{ th observation} \\[1em] = \dfrac{6}{2} \text{ th observation} \\[1em] = 3 \text{ rd observation} \\[1em] = 19.$

From set of observations, we see that:

19 has the maximum frequency.

Hence, mean = 17.8, median = 19, mode = 19.

(ii) Arranging given observations in ascending order:

7, 8, 8, 8, 9, 9, 11, 12

Sum of observations = 7 + 8 + 8 + 8 + 9 + 9 + 11 + 12 = 72

By formula,

Mean = $\dfrac{\text{Sum of observation}}{\text{No. of observation}} = \dfrac{72}{8}$ = 9

Here n = 8, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{8}{2} \text{ th observation} + \Big(\dfrac{8}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + (4 + 1) \text{ th observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + 5 \text{ th observation}}{2} \\[1em] = \dfrac{8 + 9}{2} \\[1em] = \dfrac{17}{2} \\[1em] = 8.5.$

From set of observations, we see that :

8 has the maximum frequency.

Hence, mean = 9, median = 8.5, mode = 8.

(iii) Arranging given observations in ascending order:

0, 1, 1, 2, 2, 3, 3, 3, 4, 5

Sum of observations = 0 + 1 + 1 + 2 + 2 + 3 + 3 + 3 + 4 + 5 = 24

By formula,

Mean = $\dfrac{\text{Sum of observation}}{\text{No. of observation}} = \dfrac{24}{10}$ = 2.4

Here n = 10, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{10}{2} \text{ th observation} + \Big(\dfrac{10}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + (5 + 1) \text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + 6 \text{ th observation}}{2} \\[1em] = \dfrac{2 + 3}{2} \\[1em] = \dfrac{5}{2} \\[1em] = 2.5.$

From set of observations, we see that:

3 has the maximum frequency.

Hence, mean = 2.4, median = 2.5, mode = 3.

(iv) Arranging given observations in ascending order:

6, 6, 7, 8, 10, 10, 10, 11, 13

Sum of observations = 6 + 6 + 7 + 8 + 10 + 10 + 10 + 11 + 13 = 81

By formula,

Mean = $\dfrac{\text{Sum of observation}}{\text{No. of observation}} = \dfrac{81}{9}$ = 9

Here n = 9, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{9 + 1}{2} \text{ th observation} \\[1em] = \dfrac{10}{2} \text{ th observation} \\[1em] = 5 \text{ th observation} \\[1em] = 10.$

From set of observations, we see that:

10 has the maximum frequency.

Hence, mean = 9, median = 10, mode = 10.

The marks of 10 students of a class in an examination arranged in ascending order is as follows:

13, 35, 43, 46, x, x + 4, 55, 61, 71, 80

If the median marks is 48, find the value of x. Hence, find the mode of the given data.

Answer

Here, n = 10, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{10}{2} \text{ th observation} + \Big(\dfrac{10}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + (5 + 1) \text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + 6 \text{ th observation}}{2} \\[1em]$

Median = $\dfrac{x + (x + 4)}{2}$

$\Rightarrow 48 = \dfrac{\text{x + x + 4}}{2} \\[1em] \Rightarrow 48 = \dfrac{\text{2x + 4}}{2} \\[1em] \Rightarrow 48 \times 2 = \text{2x + 4}$

⇒ 96 = 2x + 4

⇒ 2x = 96 - 4

⇒ 2x = 92

⇒ x = $\dfrac{92}{2}$

⇒ x = 46

Set of observations : 13, 35, 43, 46, 46, 50, 55, 61, 71, 80

Here, 46 has the maximum frequency.

Hence, value of x = 46 and mode = 46.

The following sizes of shoes were sold by a shop on a particular day.

8, 9, 5, 6, 4, 9, 1, 9, 3, 6, 3, 9, 7, 1, 2, 9, 5

Find the modal size of the shoes sold.

Answer

In the given data : 8, 9, 5, 6, 4, 9, 1, 9, 3, 6, 3, 9, 7, 1, 2, 9, 5

9 is repeated more number of times than any other number.

Hence, modal size of the shoes sold = 9.

The following table shows the weights of 15 students :

Calculate :

(i) mean

(ii) median

(iii) mode

Answer

The variates are already in ascending order. We construct the cumulative frequency table as under:

Total number of observations = 15, which is odd.

(i) By formula,

$\Rightarrow \text{Mean} = \dfrac{\sum\text{fx}}{\sum\text{f}} \\[1em] \Rightarrow \text{Mean} = \dfrac{796}{15} \\[1em] \Rightarrow \text{Mean} = 53.06$

Hence, mean = 53.06.

(ii) By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{15 + 1}{2} \text{ th observation} \\[1em] = \dfrac{16}{2} \text{ th observation} \\[1em] = 8 \text{ th observation} \\[1em]$

Cumulative frequencies 8th and 9th corresponds to 53 kg.

Hence, median = 53 kg.

(iii) The highest frequency is 4.

4 corresponds to two weight = 47 kg and 60 kg.

Hence, mode = 47 kg and 60 kg.

Calculate the mean, median and mode of the following distribution:

Answer

The variates are already in ascending order. We construct the cumulative frequency table as under:

Total number of observations = 20, which is even.

By formula,

$\Rightarrow \text{Mean} = \dfrac{\sum\text{fx}}{\sum\text{f}} \\[1em] \Rightarrow \text{Mean} = \dfrac{390}{20} \\[1em] \Rightarrow \text{Mean} = 19.5$

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{20}{2} \text{ th observation} + \Big(\dfrac{20}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{10 \text{ th observation} + \Big(10 + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{10 \text{ th observation} + 11 \text{ th observation}}{2} \\[1em]$

All observations from 9th to 14th are equal, each = 20

Then,

Median = $\dfrac{20 + 20}{2} = \dfrac{40}{2}$ = 20.

As the variate 20 has maximum frequency 6, so mode = 20.

Hence, mean = 19.5, median = 20, mode = 20.

In a class of 40 students, marks obtained by the students in a class test (out of 10) are given below :

Calculate the following for the given distribution :

(i) Median

(ii) Mode

Answer

The variates are already in ascending order. We construct the cumulative frequency table as under:

Total number of observations = 40, which is even.

(i) By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{40}{2} \text{ th observation} + \Big(\dfrac{40}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{20 \text{ th observation} + \Big(20 + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{20 \text{ th observation} + 21 \text{ st observation}}{2} \\[1em]$

All observations from 16th to 25th are equal, each = 6

Then,

Median = $\dfrac{6 + 6}{2} = \dfrac{12}{2}$ = 6.

Hence, median = 6.

(ii) As the variate 6 has maximum frequency 10, so mode = 6.

Hence, mode = 6.

The following table gives the daily wages of workers in a factory :

Find :

(i) the mean

(ii) the modal class

(iii) the number of workers getting daily wages below ₹ 300

(iv) the number of workers getting ₹ 260 or more but less than ₹ 340 as daily wages.

Answer

(i) We construct the following table :

By formula,

$\Rightarrow \text{Mean} = \dfrac{Σ\text{f}_{i}\text{u}_{i}}{Σ\text{f}_{i}}\\[1em] \Rightarrow \text{Mean} = \dfrac{22080}{80}\\[1em] \Rightarrow \text{Mean} = 276$

Hence, the mean is ₹ 276.

(ii) The class 220 - 240 has maximum frequency 20.

Hence, modal class = 220 - 240.

(iii) From table,

Hence, the number of workers getting daily wages below ₹ 300 = 54.

(iv) From table,

Hence, the number of workers getting ₹ 260 or more but less than ₹ 340 as daily wages = 72 - 35 = 37.

For the following frequency distribution, draw a histogram. Hence, calculate the mode.

Answer

Steps :

1. Take 1 cm along x-axis = 5 marks and 1 cm along y-axis = 5 units (frequency).

2. Construct rectangles corresponding to the given data.

3. In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

4. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 21.50

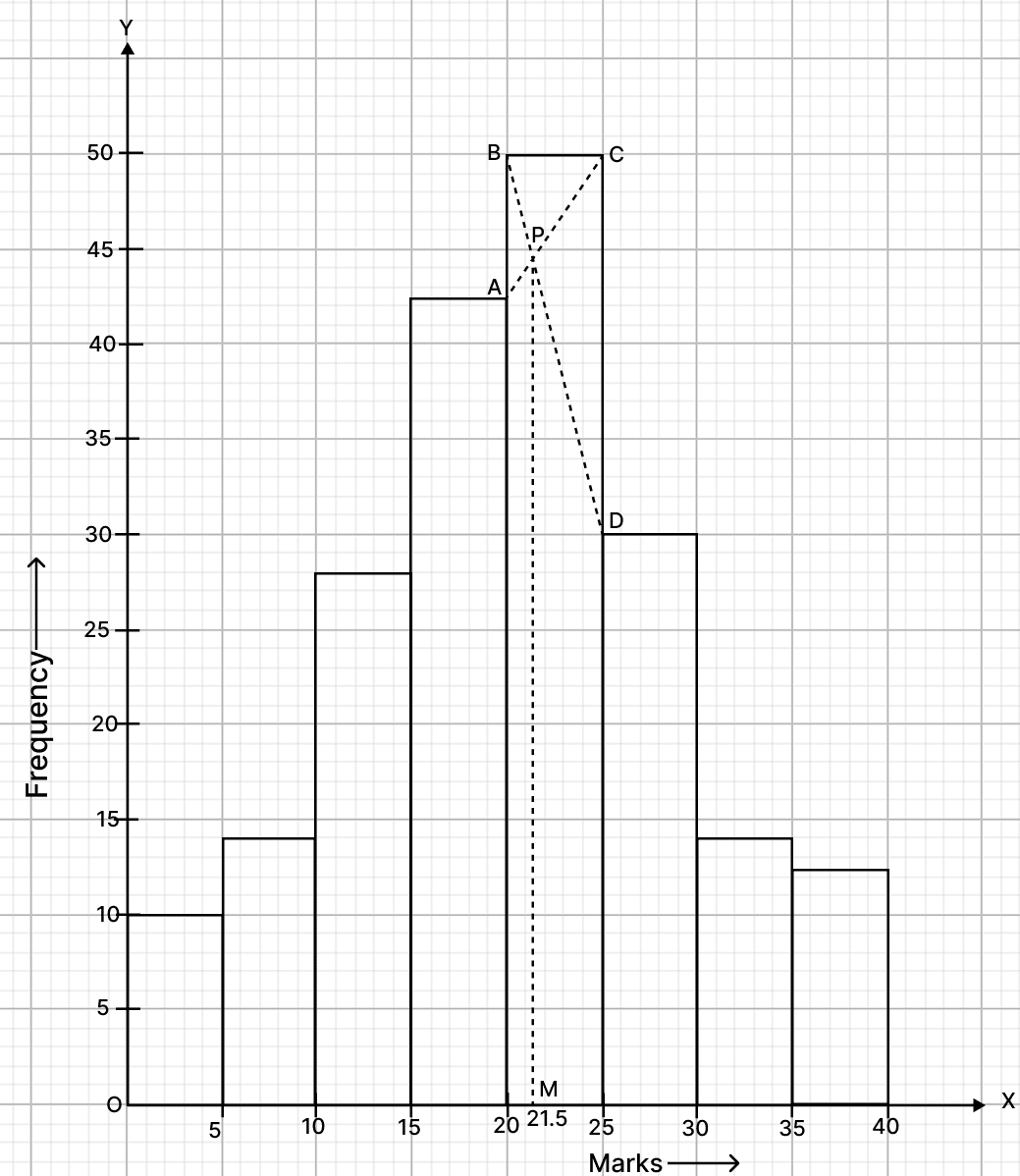
Hence, the required mode = 21.50.

Draw a histogram and hence estimate the mode for the following distribution.

Answer

Steps :

1. Take 1 cm along x-axis = 5 units and 1 cm along y-axis = 4 units.

2. Construct rectangles corresponding to the given data.

3. In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

4. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 14.

Hence, the required mode = 14.

IQ of 50 students was recorded as follows:

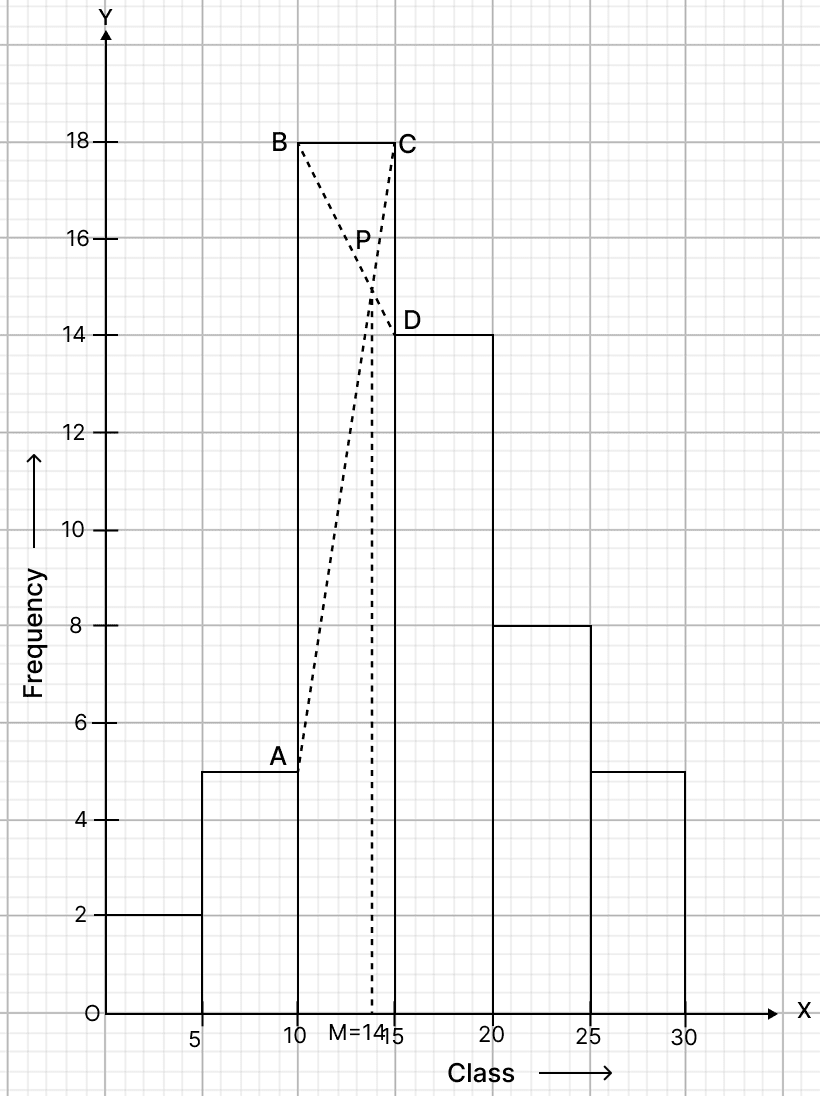
Draw a histogram for the above data and estimate the mode.

Answer

Steps :

1. Take 1 cm along x-axis = 10 scores and 1 cm along y-axis = 4 (students).

2. Since, the scale on x-axis starts at 80, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 80 and not at origin itself.

3. Construct rectangles corresponding to the given data.

4. In highest rectangle, draw two straight lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

5. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 107.

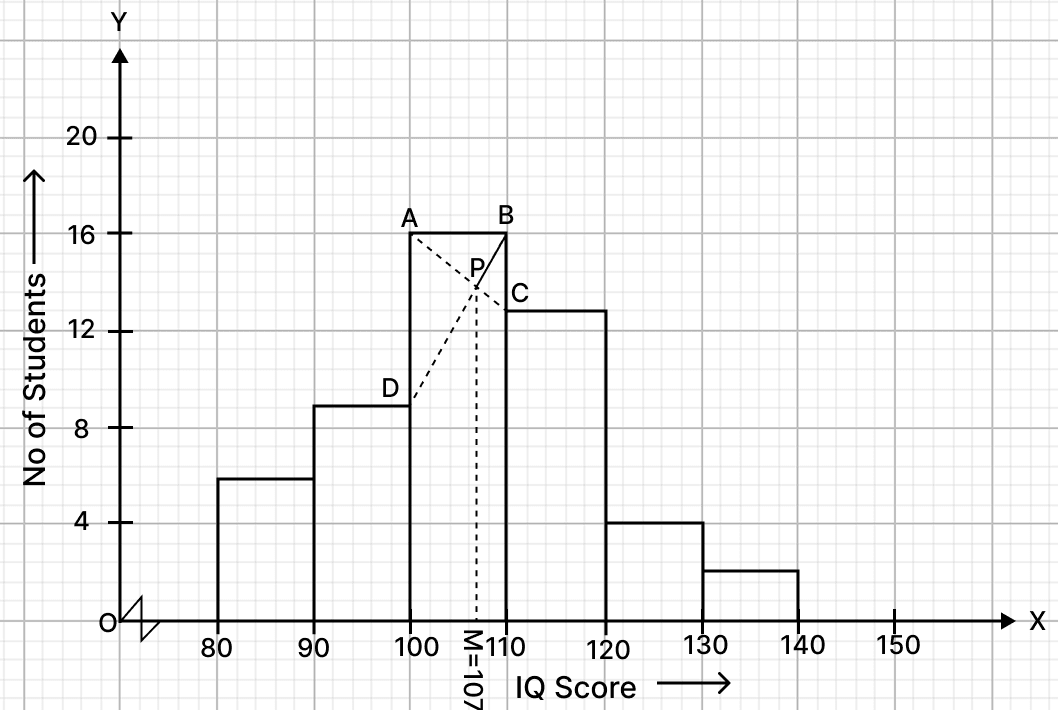
Hence, the required mode = 107.

For the following distribution, draw a histogram :

From the histogram, estimate the mode.

Answer

Steps :

1. The given frequency distribution is discontinuous, to convert it into continuous distribution,

Adjustment factor = $\dfrac{48 - 47}{2} = \dfrac{1}{2}$ = 0.5

We construct the continuous frequency table for the given data :

2. Take 2 cm along x-axis = 4 kg and 1 cm along y-axis = 4 (frequency).

3. Since, the scale on x-axis starts at 43.5, a break (zig-zag curve) is shown near the origin along x-axis to indicate that the graph is drawn to scale beginning at 43.5 and not at origin itself.

4. Construct rectangles corresponding to the given data.

5. In highest rectangle, draw two straight lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

6. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 53 kg.

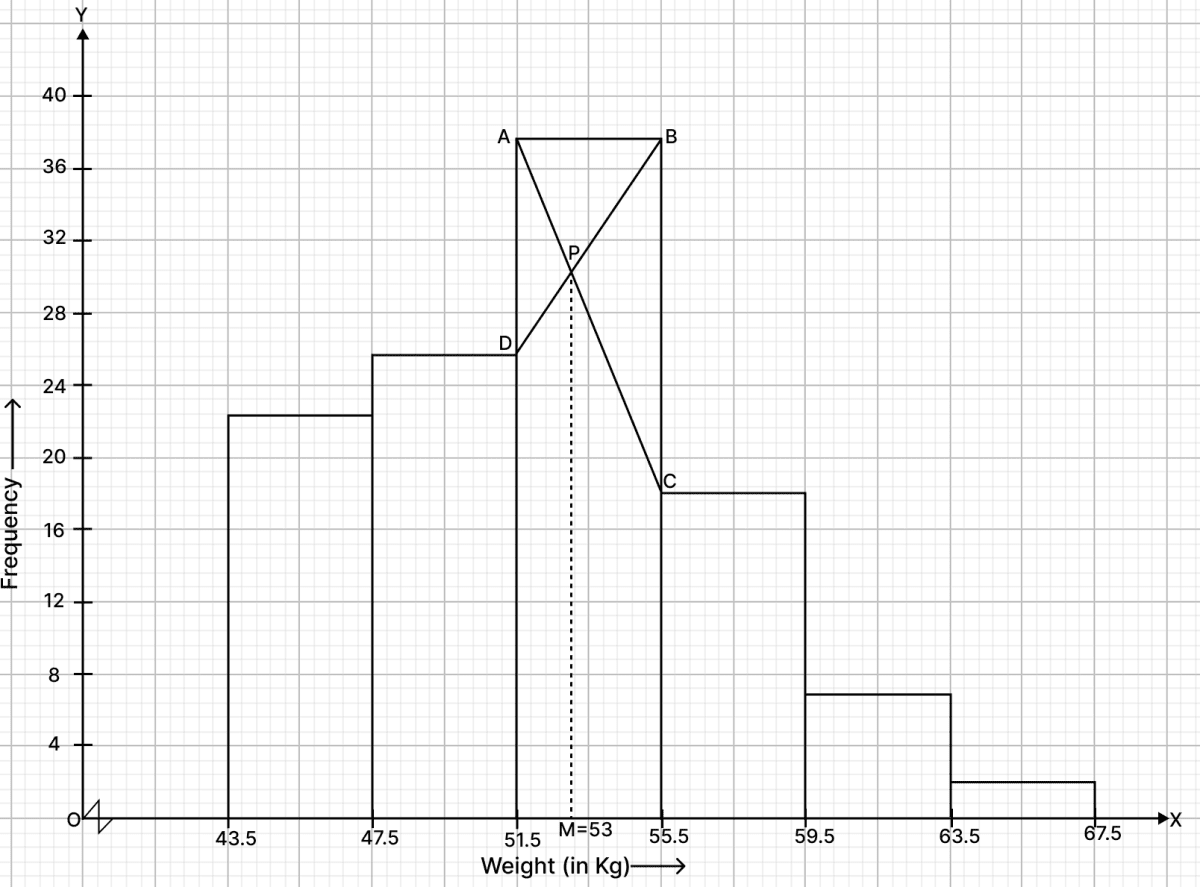
Hence, the required mode = 53.

Using a graph paper, draw a histogram for the given distribution showing the number of runs scored by 50 batsmen. From the histogram, estimate the mode of the data:

Answer

Steps :

1. Take 1 cm along x-axis = 1000 runs and 1 cm along y-axis = 4(batsman).

2. Construct rectangles corresponding to the given data.

3. In highest rectangle, draw two st. lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

4. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 4600.

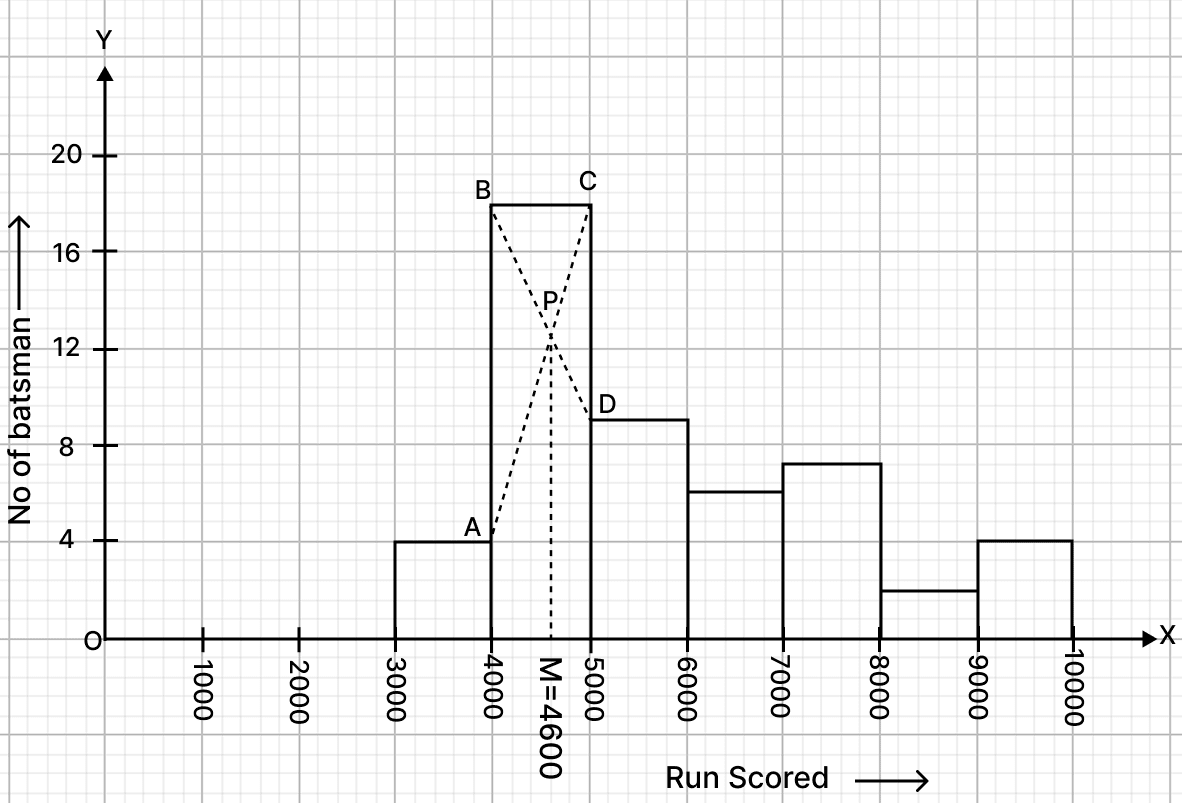
Hence, the required mode = 4600 runs.

Draw a histogram for the given data, using a graph paper.

Estimate the mode from the graph.

Answer

Steps :

1. Take 1 cm along x-axis = 1000 rupees and 1 cm along y-axis = 2 (No. of people).

2. Construct rectangles corresponding to the given data.

3. In highest rectangle, draw two straight lines AD and BC from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AD and BC.

4. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 5400.

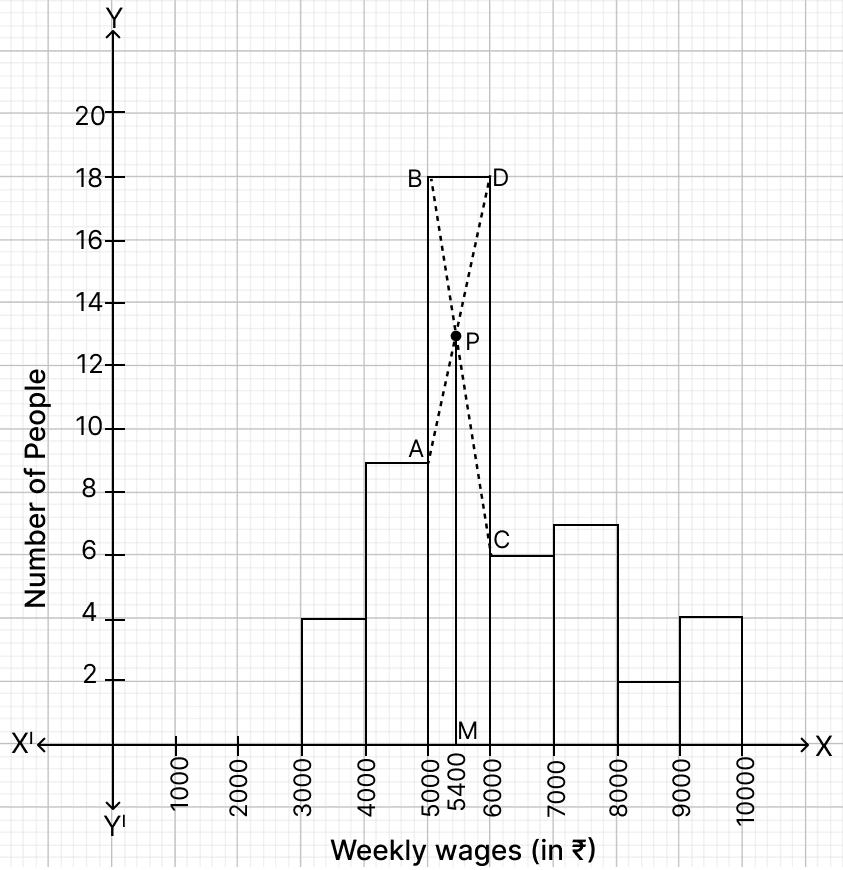
Hence, mode = ₹ 5,400.

Marks obtained by 100 students in an examination are given below:

Draw a histogram for the given data using a graph paper and find the mode. Take 2 cm = 10 marks along one axis and 2 cm = 10 students along the other axis.

Answer

Steps :

1. Take 2 cm along x-axis = 10 marks and 2 cm along y-axis = 10 students (frequency).

2. Construct rectangles corresponding to the given data.

3. In highest rectangle, draw two straight lines AC and BD from corners of the rectangles on either side of the highest rectangle to the opposite corners of the highest rectangle. Let P be the point of intersection of AC and BD.

4. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 35.

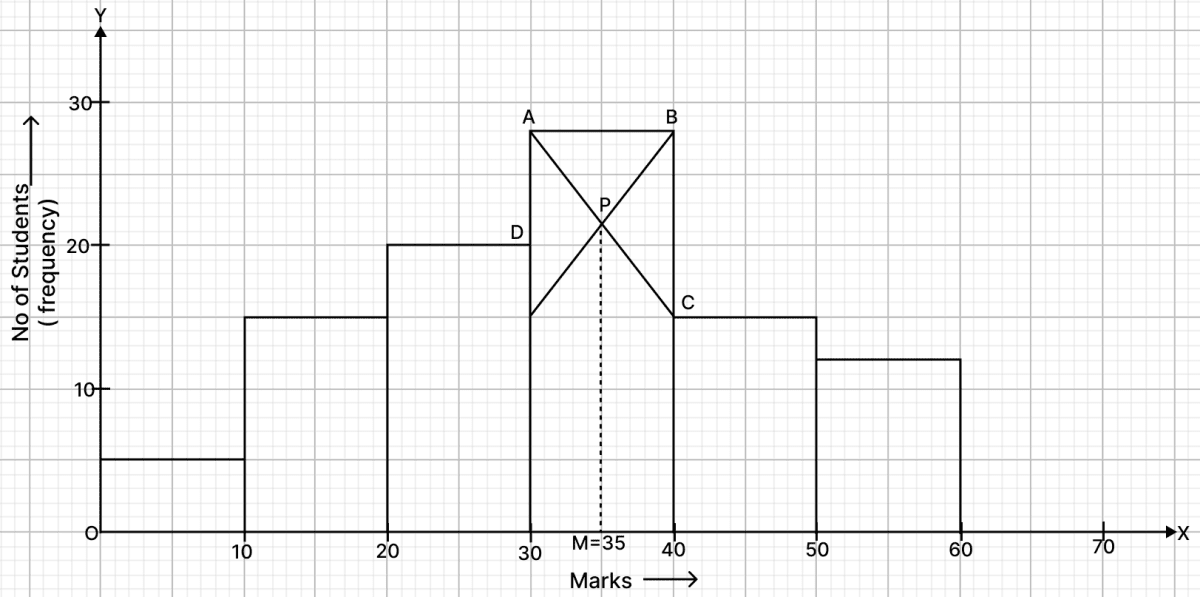
Hence, the required mode = 35.

The following distribution gives the daily wages of 60 workers of a factory.

Use graph paper to answer this question.

Take 2 cm = ₹ 100 along one axis and 2 cm = 2 workers along the other axis. Draw a histogram and hence find the mode of the given distribution.

Answer

Steps of construction :

1. Draw a histogram of the given distribution.

2. Inside the highest rectangle, which represents the maximum frequency (or modal class), draw two lines AC and BD diagonally from the upper corners C and D of adjacent rectangles.

3. Through the point K (the point of intersection of diagonals AC and BD), draw KL perpendicular to the horizontal axis.

4. The value of point L on the horizontal axis represents the value of mode.

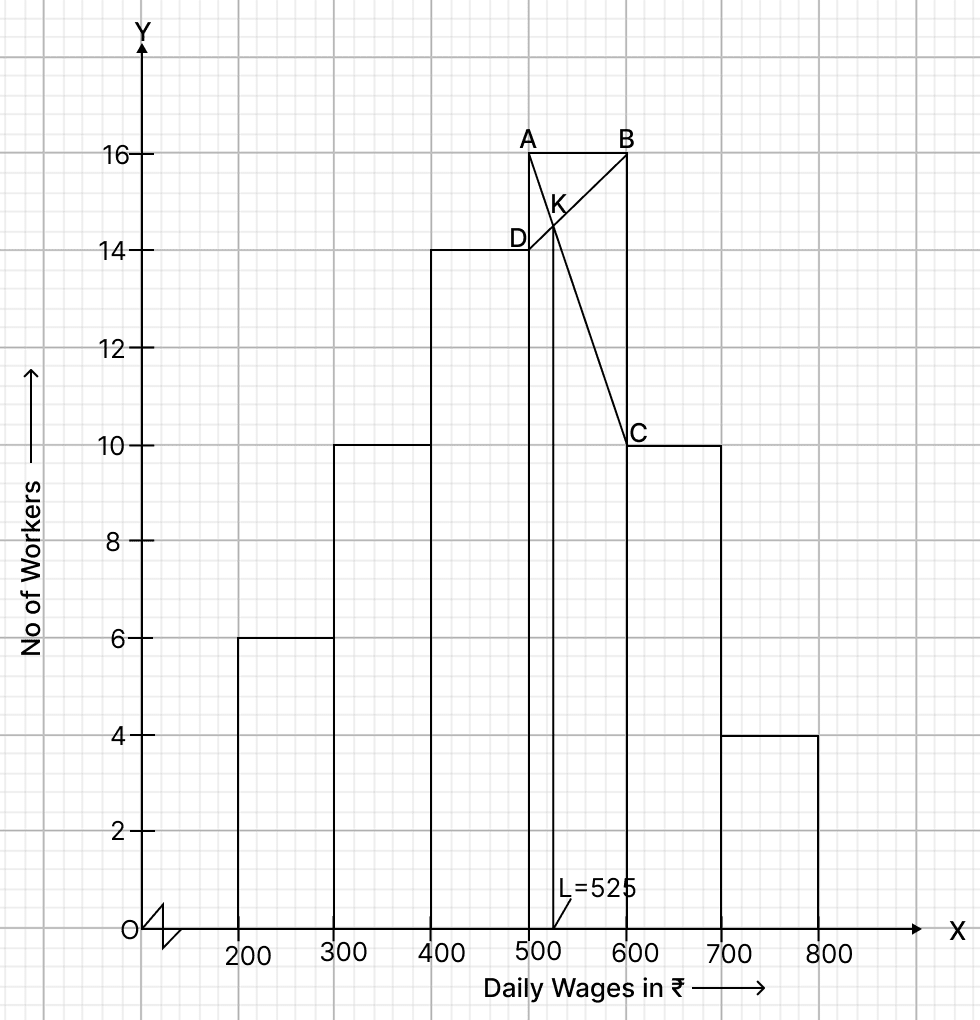
From graph,

L = ₹ 525

Hence, required mode = ₹ 525.

Choose the correct option :

A data has 35 observations arranged in a descending order. Which organization represents the median?

1. 16th

2. 17th

3. 18th

4. 19th

Answer

We know that,

The value of the middle-most observation obtained after arranging the data in an ascending order, is called median of the data.

Here no. of observations, n = 35

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{35 + 1}{2} \text{ th observation} \\[1em] = \dfrac{36}{2} \text{ th observation} \\[1em] = 18 \text{ th observation}$

Since, given data is arranged in descending order,

Median = 18 th observation.

Hence, Option 3 is the correct option.

The median of first 8 prime numbers is:

1. 7

2. 9

3. 11

4. 13

Answer

Prime numbers : 2, 3, 5, 7, 11, 13, 17, 19

No. of terms (n) = 8, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

Substituting values we get:

$= \dfrac{\dfrac{8}{2} \text{ th observation} + \Big(\dfrac{8}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + \Big(4 + 1\Big) \text{ rth observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + 5 \text{ th observation}}{2} \\[1em] = \dfrac{7 + 11}{2} \\[1em] = \dfrac{18}{2} \\[1em] = 9.$

Hence, Option 2 is the correct option.

If the median height of the students of a class is 105 cm, it means that

1. the average height of the students of the class is 105 cm

2. maximum number of students in the class are 105 cm tall

3. there are as many students in the class, taller than 105 cm as are shorter than 105 cm

4. none of these

Answer

We know that,

The value of the middle-most observation obtained after arranging the data in an ascending order, is called median of the data.

Hence, Option 3 is the correct option.

If the median of the data 4, 7, x - 1, x - 3, 16, 25, written in ascending order, is 13, then x is equal to :

1. 13

2. 14

3. 15

4. 16

Answer

Here, n = 6, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$\Rightarrow 13 = \dfrac{\dfrac{6}{2} \text{ th observation} + \Big(\dfrac{6}{2} + 1\Big) \text{ th observation}}{2} \\[1em] \Rightarrow 13 = \dfrac{3 \text{ rd observation} + \Big(3 + 1\Big) \text{ th observation}}{2} \\[1em] \Rightarrow 13 \times 2 = 3 \text{ rd observation} + 4 \text{ th observation} \\[1em]$

⇒ 26 = (x - 1) + (x - 3)

⇒ 26 = 2x - 4

⇒ 2x = 26 + 4

⇒ 2x = 30

⇒ x = $\dfrac{30}{2}$

⇒ x = 15.

Hence, Option 3 is the correct option.

If 25 is removed from the data 20, 24, 25, 26, 27, 28, 29, 30, then the median increases by:

1. 0.5

2. 1

3. 1.5

4. 2

Answer

Set of observations = 20, 24, 25, 26, 27, 28, 29, 30

Here, n = 8, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{8}{2} \text{ th observation} + \Big(\dfrac{8}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + \Big(4 + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{4 \text{ th observation} + 5 \text{ th observation}}{2} \\[1em] = \dfrac{26 + 27}{2} \\[1em] = \dfrac{53}{2} \\[1em] = 26.5$

If 25 is removed from given set, then we get:

Set of observations = 20, 24, 26, 27, 28, 29, 30

Here, n = 7, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{7 + 1}{2} \text{ th observation} \\[1em] = \dfrac{8}{2} \text{ th observation} \\[1em] = 4 \text{ th observation} \\[1em] = 27$

Difference between median = 27 - 26.5 = 0.5

Hence, Option 1 is the correct option.

The mean of 4, 5, 1, 3, 7, 4 is x. The numbers 2, 4, 3, 2, 3, y, 3 have mean x - 1 and median z. Then, y + z = ?

options

1. 4

2. 5

3. 6

4. 7

Answer

Given,

Mean of 4, 5, 1, 3, 7, 4 is x.

Sum of observations = 4 + 5 + 1 + 3 + 7 + 4 = 24

Mean (x) = $\dfrac{\text{Sum of observations}}{\text{No. of observations}} = \dfrac{24}{6}$ = 4.

Given,

Numbers 2, 4, 3, 2, 3, y, 3 have mean x - 1 = 4 - 1 = 3.

Sum of observations = 2 + 4 + 3 + 2 + 3 + y + 3 = 17 + y

Mean (x) = $\dfrac{\text{Sum of observations}}{\text{No. of observations}} = \dfrac{17 + \text{y}}{7}$

$\Rightarrow 3 = \dfrac{17 + \text{y}}{7}$

⇒ 7 × 3 = 17 + y

⇒ 21 = 17 + y

⇒ y = 21 - 17

⇒ y = 4

Observations in ascending order are = 2, 2, 3, 3, 3, 4, 4

Here, n = 7, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{7 + 1}{2} \text{ th observation} \\[1em] = \dfrac{8}{2} \text{ th observation} \\[1em] = 4 \text{ th observation} \\[1em] = 3$

∴ z = 3.

y + z = 4 + 3 = 7.

Hence, Option 4 is the correct option.

Which measure of central tendency would be the most appropriate for a shoe dealer to determine the quantity of different sizes that he should order?

1. Mean

2. Median

3. Mode

4. Any of these

Answer

Mode represents the value that occurs most frequently in a dataset.

The mode will determine the most frequently sold shoe size in the shop.

Hence, Option 3 is the correct option.

Which of the following cannot be determined graphically?

1. Mean

2. Median

3. Mode

4. None of these

Answer

We know that,

To determine mean we do not need any graphical method, since, it relies on the exact numerical value of every single observation in a dataset and graphs like histograms or frequency polygons represent data in ranges, specific individual values to determine mean is not possible.

Hence, Option 1 is the correct option.

The median of a frequency distribution is found graphically with the help of

1. Ogive

2. Histogram

3. Frequency polygon

4. Bar graph

Answer

The median of a grouped frequency distribution is typically found graphically using a cumulative frequency curve, also known as an ogive.

Hence, Option 1 is the correct option.

The median of 0, 2, 2, 2, -3, 5, -1, 5, 5, -3, 6, 6, 5, 6 is :

1. -1.5

2. 0

3. 2

4. 3.5

Answer

Given,

Set of observations = 0, 2, 2, 2, -3, 5, -1, 5, 5, -3, 6, 6, 5, 6

Arranging the numbers in ascending order :

-3, -3, -1, 0, 2, 2, 2, 5, 5, 5, 5, 6, 6, 6.

Here n = 14, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{14}{2} \text{ th observation} + \Big(\dfrac{14}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{7 \text{ th observation} + \Big(7 + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{7 \text{ th observation} + 8 \text{ th observation}}{2} \\[1em] = \dfrac{2 + 5}{2} \\[1em] = \dfrac{7}{2} \\[1em] = 3.5$

Hence, Option 4 is the correct option.

The median of the following data is:

1. 30

2. 31

3. 35

4. 40

Answer

Cumulative frequency distribution table is:

Here, n = 11, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{11 + 1}{2} \text{ th observation} \\[1em] = \dfrac{12}{2} \text{ th observation} \\[1em] = 6 \text{ th observation}$

From table,

6th observation corresponds to 30.

∴ Median = 30

Hence, Option 1 is the correct option.

Consider the following table :

The median of the above frequency distribution is :

1. 122 mm

2. 122.5 mm

3. 122.75 mm

4. 123 mm

Answer

Cumulative frequency distribution table is as follows :

Here n = 50, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{50}{2} \text{ th observation} + \Big(\dfrac{50}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{25 \text{ th observation} + \Big(25 + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{25 \text{ th observation} + 26 \text{ th observation}}{2} \\[1em] = \dfrac{122 + 122}{2} \\[1em] = \dfrac{244}{2} \\[1em] = 122 \text{ mm}.$

Since, all observations from 25th to 26th corresponds to 122 mm.

Hence, Option 1 is the correct option.

Consider the following table:

The upper limit of the median class is :

1. 10

2. 15

3. 20

4. 25

Answer

We construct the cumulative frequency distribution table as under :

Here n = 70, which is even.

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{ th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{ th observation}}{2}$

$= \dfrac{\dfrac{70}{2} \text{ th observation} + \Big(\dfrac{70}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{35 \text{ th observation} + \Big(35 + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{35 \text{th observation} + 36 \text{ th observation}}{2}$

As observation from 19th to 37th lies in the class 10 - 15

∴ Median class = 10 - 15, with upper limit = 15

Hence, Option 2 is the correct option.

The marks secured (out of 10) by a student in 15 unit tests are as follows:

5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 8, 7, 9, 10, 8

The mode of the above data is :

1. 5

2. 7

3. 8

4. 10

Answer

From above set of numbers : 8 occurs most of the time.

Mode = 8.

Hence, Option 3 is the correct option.

Average value of the median of 2, 8, 3, 7, 4, 6, 1 and the mode of 2, 9, 3, 4, 9, 6, 9 is:

1. 6

2. 6.5

3. 8

4. 9

Answer

Arranging set of observations in ascending order : 1, 2, 3, 4, 6, 7, 8

Here, n = 7, which is odd.

By formula,

Median = $\dfrac{\text{n} + 1}{2} \text{ th observation}$

$= \dfrac{7 + 1}{2} \text{ th observation} \\[1em] = \dfrac{8}{2} \text{ th observation} \\[1em] = 4 \text{ th observation} \\[1em] = 4$

Given,

2, 9, 3, 4, 9, 6, 9

From above set of numbers : 9 occurs most of the time.

Mode = 9.

Average of median and mode = $\dfrac{9 + 4}{2} = \dfrac{13}{2}$ = 6.5

Hence, Option 2 is the correct option.

The mode of a frequency distribution can be determined graphically from :

1. Histogram

2. Frequency polygon

3. Ogive

4. Bar graph

Answer

The mode of a frequency distribution can be determined graphically from Histogram.

Hence, Option 1 is the correct option.

If the mode of the following data is 7, the value of k is :

2, 4, 6, 7, 5, 6, 10, 6, 7, 2k + 1, 9, 7, 13

1. 2

2. 3

3. 4

4. 7

Answer

Given, mode = 7

From above set of numbers : 6 and 7 occurs most of the time (3 times each). For 7 to be the mode, its frequency must be greater than that of 6.

Therefore, the unknown expression 2k + 1 must be equal to 7.

⇒ 2k + 1 = 7

⇒ 2k = 7 - 1

⇒ 2k = 6

⇒ k = $\dfrac{6}{2}$

⇒ k = 3.

Hence, Option 2 is the correct option.

The lower limit of the modal class of the following data is:

1. 10

2. 20

3. 30

4. 40

Answer

Since the class 20 - 30 has highest frequency i.e. 13.

∴ Modal class = 20 - 30.

The lower limit of the modal class = 20.

Hence, Option 2 is the correct option.

Consider the following distribution :

The sum of lower limits of the median class and the modal class is :

1. 15

2. 25

3. 30

4. 35

Answer

We construct the cumulative frequency distribution table as under :

Here n (total no. of observations) = 66.

As n is even,

By formula,

Median = $\dfrac{\dfrac{\text{n}}{2} \text{th observation} + \Big(\dfrac{\text{n}}{2} + 1\Big) \text{th observation}}{2}$

$= \dfrac{\dfrac{66}{2} \text{th observation} + \Big(\dfrac{66}{2} + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{33 \text{th observation} + \Big(33 + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{33 \text{th observation} + 34 \text{th observation}}{2}$