The square of -8 is:
-16
16
-64
64
Answer
Hence, option 4 is the correct option.
is equal to:
4
-4
2
0
Answer
Hence, option 2 is the correct option.
Square root of 2.50 x 103 is:
5
125
50
none of the above
Answer
Hence, option 3 is the correct option.
The smallest natural number which on multiplying with 48 gives a perfect square number is:
12
3
none of the above
Answer
Finding prime factors of 48
48 = (2 x 2) x (2 x 2) x 3
Since the prime factor 3 is not in pair.
The given number should be multiplied by 3.
Hence, option 2 is the correct option.
The smallest natural number by which should 175 be divided to get a perfect square number is:
5
7
15
none of the above
Answer
Finding prime factors of 175
175 = (5 x 5) x 7
Since the prime factor 7 is not in pair.
The given number should be divided by 7.
Hence, option 2 is the correct option.
Find the square of 59.
Answer
Find the square of 6.3.
Answer
Find the square of
Answer
By splitting into prime factors, find the square root of 11025.
Answer
Square root of 11025 is 105.
By splitting into prime factors, find the square root of 396900.
Answer
Square root of 396900 is 630.
By splitting into prime factors, find the square root of 194481.
Answer
Square root of 194481 is 441.
Find the smallest number by which 2592 be multiplied so that the product is a perfect square.
Answer
Finding prime factors of 2592
Since the prime factor 2 is not in pair.
2 should be multiplied with 2592 so that the product is a perfect square.
Find the smallest number by which 12748 be multiplied so that the product is a perfect square.
Answer
Finding prime factors of 12748
Since the prime factor 3187 is not in pair.
3187 should be multiplied with 12748 so that the product is a perfect square.
Find the smallest number by which 10368 be divided so that the result is a perfect square. Also, find the square root of the resulting number.
Answer
Finding prime factors of 10368
Since the prime factor 2 is not in pair.
2 should be divided by 10368 so that the 5184 is a perfect square and square root of 5184 is 72.
Find the square root of 0.1764.
Answer
Find the square root of .
Answer
Find the square root of 0.0169.
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
Evaluate:
Answer
LCM of 4 and 10 is 2 x 2 x 5 = 20.
Evaluate:
Answer
A man, after a tour, finds that he had spent every day as many rupees as the number of days he had been on tour. How long did his tour last, if he had spent in all ₹1,296?
Answer
Let number of days he had been on tour be .
Rupees spent every day = number of days he had been on tour =
Total rupees spent = ₹1,296
Hence,
So, the man was on tour for 36 days.
Out of 745 students, maximum are to be arranged in the school field for a P.T. display, such that the number of rows is equal to the number of columns. Find the number of rows if 16 students were left out after the arrangement.
Answer
Let the number of columns be .
The number of rows = the number of columns =
Students arranged in P.T. display = 745 - 16 = 729
Hence,
Hence, the number of rows = 27.
13 and 31 is a strange pair of numbers such that their square 169 and 961 are also mirror images of each other. Find two more such pairs.
Answer
12 and 21 are mirror images of each other.
And, 144 and 441 are mirror images of each other.
102 and 201 are mirror images of each other.
And, 10404 and 40401 are mirror images of each other.
12 and 21; 102 and 201 are 2 such pairs.
Find the smallest perfect square divisible by 3, 4, 5 and 6.
Answer
LCM of 3, 4, 5 and 6 is 2 x 2 x 3 x 5 = 60
As 3 and 5 are not in pair. To make it a perfect square, it must be multiplied with 3 x 5 = 15.
So, required perfect square = .
If , find the value of
Answer
.
If , find the value of
Answer
If ; the value of is:
1.12
4.48
2.24 x 4
none of the above
Answer
If , then
Hence, option 2 is the correct option.
If ; the value of is:
527
52.7
0.527
none of the above
Answer
If , then
Hence, option 2 is the correct option.
n is the least natural number that must be added to 23 so that the resulting number is a perfect square, the value of n is:
7
2
5
-7
Answer
Since 42 < 23 < 52,
The least number that must be added to 23 to make the resulting number a perfect square = 52 - 23 = 25 - 23 = 2.
Hence, option 2 is the correct option.
n is the least natural number that must be subtracted from 23 so that the resulting number is a perfect square, the value of n is:
7
2
5
-7
Answer
Since 42 < 23 < 52,
The least number that must be subtracted from 23 to make the resulting number a perfect square = 23 - 42 = 23 - 16 = 7.
Hence, option 1 is the correct option.
Find the square root of 4761.
Answer
Square root of 4761 by division method:
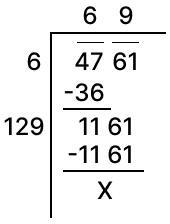
Find the square root of 7744.
Answer
Square root of 7744 by division method:
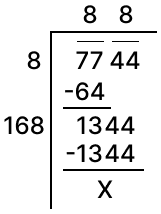
Find the square root of 15129.
Answer
Square root of 15129 by division method:
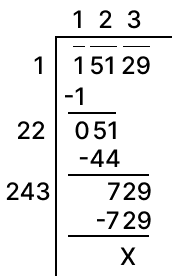
Find the square root of 0.2916.
Answer
Square root of 0.2916 by division method:
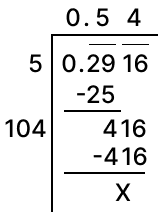
Find the square root of 0.001225.
Answer
Square root of 0.001225 by division method:
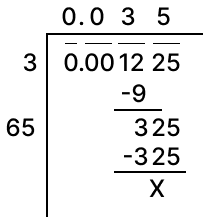
Find the square root of 0.023104.
Answer
Square root of 0.023104 by division method:
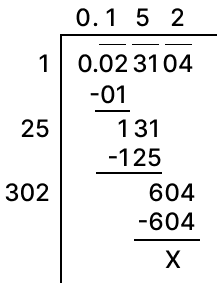
Find the square root of 27.3529.
Answer
Square root of 27.3529 by division method:
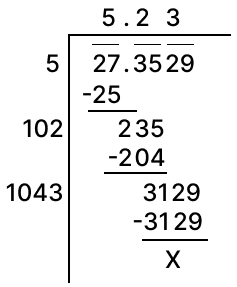
Find the square root of 4.2025.
Answer
Square root of 4.2025 by division method:
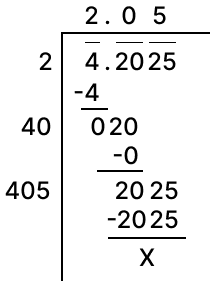
Find the square root of 531.7636.
Answer
Square root of 531.7636 by division method:
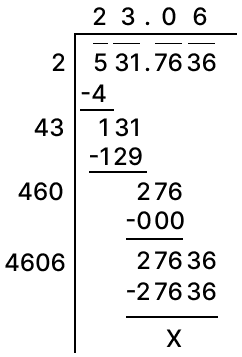
Find the square root of 0.007225.
Answer
Square root of 0.007225 by division method:

Find the square root of 245 correct to two places of decimal.
Answer
Square root of 245 correct to two places of decimal by division method:
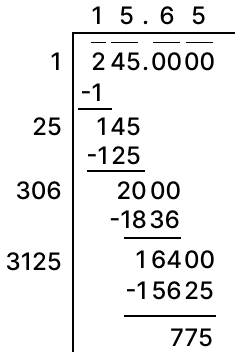
Find the square root of 496 correct to three places of decimal.
Answer
Square root of 496 correct to three places of decimal by division method:

Find the square root of 82.6 correct to two places of decimal.
Answer
Square root of 82.6 correct to two places of decimal by division method:

Find the square root of 0.065 correct to three places of decimal.
Answer
Square root of 0.065 correct to three places of decimal by division method:
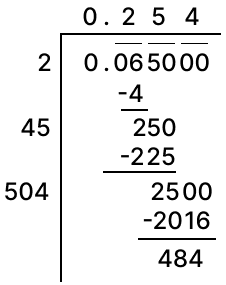
Find the square root of 5.2005 correct to two places of decimal.
Answer
Square root of 5.2005 correct to two places of decimal by division method:
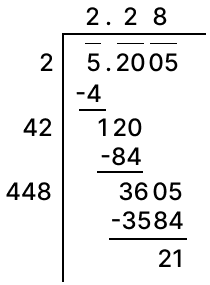
Find the square root of 0.602 correct to two places of decimal.
Answer
Square root of 0.602 correct to two places of decimal by division method:
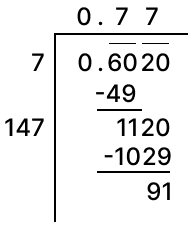
Find the square root of correct to two decimal places.
Answer
Square root of 3.8 correct to two places of decimal by division method:
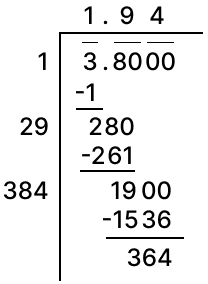
Find the square root of correct to two decimal places.
Answer
Square root of 6.875 correct to two places of decimal by division method:

For each of the following, find the least number that must be subtracted so that the resulting number is a perfect square.
796
Answer
Using division method:

Clearly, if 12 is subtracted from 796, the remainder will be a perfect square.
Since, 796 - 12 = 784
and,
Hence, 12 should be subtracted from 796.
For each of the following, find the least number that must be subtracted so that the resulting number is a perfect square.
1886
Answer
Using division method:
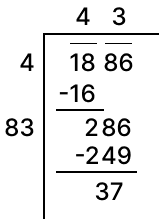
Clearly, if 37 is subtracted from 1886, the remainder will be a perfect square.
Since, 1886 - 37 = 1849
and,
Hence, 37 should be subtracted from 1886.
For each of the following, find the least number that must be subtracted so that the resulting number is a perfect square.
23497
Answer
Using division method:
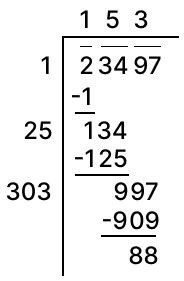
Clearly, if 88 is subtracted from 23497, the remainder will be a perfect square.
Since, 23497 - 88 = 23409
and,
Hence, 88 should be subtracted from 23497.
For each of the following, find the least number that must be added so that the resulting number is a perfect square.
511
Answer
Using division method:
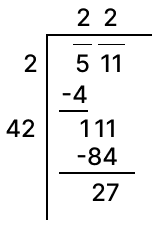
Clearly, 511 is greater than 222.
∴ On adding the required number to 511, we shall be getting 232 i.e, 529.
So, the required number = 529 - 511 = 18.
Hence, 18 should be added to 511.
For each of the following, find the least number that must be added so that the resulting number is a perfect square.
7172
Answer
Using division method:
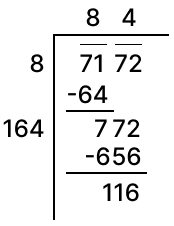
Clearly, 7172 is greater than 842.
∴ On adding the required number to 7172, we shall be getting 852 i.e, 7225.
So, the required number = 7225 - 7172 = 53.
Hence, 53 should be added to 7172.
For each of the following, find the least number that must be added so that the resulting number is a perfect square.
55078
Answer
Using division method:

Clearly, 55078 is greater than 2352.
∴ On adding the required number to 55078, we shall be getting 2352 i.e, 55225.
So, the required number = 55225 - 55078 = 147.
Hence, 147 should be added to 55078.
Find the square root of 7 correct to two decimal places; then use it to find the value of correct to three significant digits.
Answer
Square root of 7 correct to two decimal places using division method:
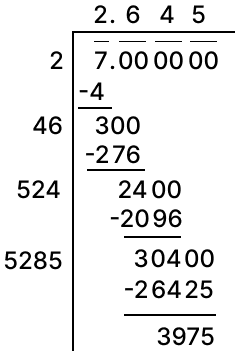
Putting the value of , we get
Hence, and .
Find the value of correct to 2 decimal places; then use it to find the square root of correct to 2 significant digits.
Answer
Square root of 5 correct to two decimal places using division method:
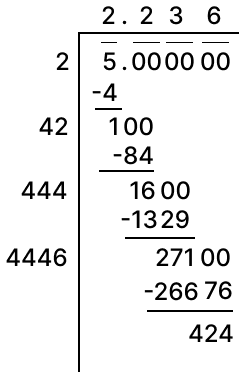
Putting the value of ,we get
Hence, and .
Find the square root of .
Answer
Square root of 1764 using division method:
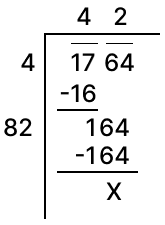
Square root of 2809 using division method:
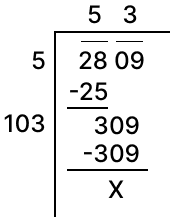
Find the square root of .
Answer
Square root of 169 using division method:
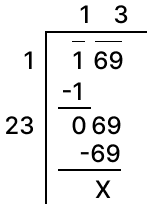
Square root of 1369 using division method:
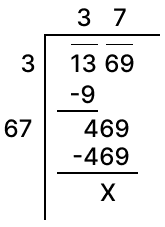
Find the square root of .
Answer
Hence, .
Find the square root of 0.01 + .
Answer
Hence, 0.01 +
Find the square root of 7.832 correct to 2 decimal places.
Answer
Square root of 7.832 correct to two places of decimal by division method:
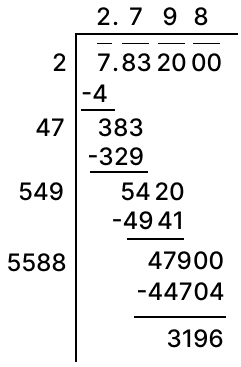
Find the square root of 7.832 correct to 2 significant digits.
Answer
Square root of 7.832 correct to two significant digits by division method:
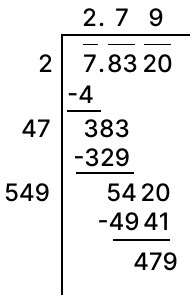
Find the least number which must be subtracted from 1205 so that the resulting number is a perfect square.
Answer

∴ If 49 is subtracted from 1205, the resulting number will be a perfect square.
Hence, 49 should be subtracted from 1205.
Find the least number which must be added to 1205 so that the resulting number is a perfect square.
Answer

Clearly, 1205 is greater than 342.
∴ On adding the required number to 1205, we shall be getting 352 i.e, 1225
So, the required number = 1225 - 1205 = 20.
Hence, 20 should be added to 1205.
Find the least number which must be subtracted from 2037 so that the resulting number is a perfect square.
Answer
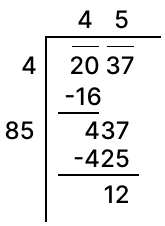
∴ If 12 is subtracted from 2037, the resulting number will be a perfect square.
Hence, 12 should be subtracted from 2025.
Find the least number which must be added to 5483 so that the resulting number is a perfect square.
Answer
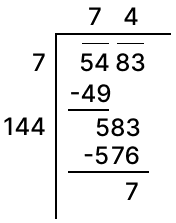
Clearly, 5483 is greater than 742.
∴ On adding the required number to 5483, we shall be getting 752 i.e, 5625
So, the required number = 5625 - 5483 = 142.
Hence, 142 should be added to 5483.
The value of 182 - 172 is :
1
-1
35
none of the above
Answer
According to the property of square numbers, for any natural number n,
Hence, option 3 is the correct option.
The sum of first four odd natural numbers is :
23
24
43
44
Answer
As we know that, the sum of first n odd natural numbers = n2.
Hence, option 2 is the correct option.
242 has n at its unit place, the value of n is:
4
16
576
6
Answer
According to the property of square numbers, if the digit at the unit's place of a number is 4 or 6, then its square will always have 6 at its unit's place.
Hence, option 4 is the correct option.
A number ends with 5 zeros, the number of zeros in its square will be :
5
25
10
8
Answer
According to the property of square numbers, if a number ends with n zeroes, its square ends with 2n zeroes.
So, if a number ends with 5 zeroes, its square ends with 2 x 5 = 10 zeroes.
Hence, option 3 is the correct option.
Seeing the value of the digit at unit's place, state which of the following can be square of a number ?
(i) 3051
(ii) 2332
(iii) 5684
(iv) 6908
(v) 50699
Answer
According to the property of square numbers, the ending digit of the square of a number is 0, 1, 4, 5, 6 or 9.
Hence, (i) 3051, (iii) 5684 and (v) 50699 can be square of a number.
Squares of which of the following numbers will have 1 (one) at their unit's place ?
(i) 57
(ii) 81
(iii) 139
(iv) 73
(v) 64
Answer
According to the property of square number, if a number has 1 or 9 in its unit's place, then square of this number always has 1 at its unit place.
Hence, (ii) 81 and (iii) 139 will have 1 at their unit's place.
Which of the following numbers will not have 1 (one) at their unit's place ?
(i) 322
(ii) 572
(iii) 692
(iv) 3212
(v) 2652
Answer
According to the property of square number, if a number has 1 or 9 in its unit's place, then square of this number always has 1 at its unit place.
Hence, (i) 322, (ii) 572 and (v) 2652 will not have 1 at their unit's place.
Squares of which of the following numbers will not have 6 at their unit's place ?
(i) 35
(ii) 23
(iii) 64
(iv) 76
(v) 98
Answer
According to the property of square number, if a number has 4 or 6 in its unit's place, then square of this number always has 6 at its unit place.
Hence, (i) 35, (ii) 23 and (v) 98 will not have 6 at their unit's place.
Which of the following numbers will have 6 at their unit's place :
(i) 262
(ii) 492
(iii) 342
(iv) 432
(v) 2442
Answer
According to the property of square number, if a number has 4 or 6 in its unit's place, then square of this number always has 6 at its unit place.
Hence, (i) 262, (iii) 342 and (v) 2442 will have 6 at their unit's place.
If a number ends with 3 zeroes, how many zeroes will its square have ?
Answer
According to the property of square numbers, if a number ends with n zeroes, its square ends with 2n zeroes.
So, if a number ends with 3 zeroes, its square ends with 2 x 3 = 6 zeroes.
If the square of a number ends with 10 zeroes, how many zeroes will the number have ?
Answer
According to the property of square numbers, if a number ends with n zeroes, its square ends with 2n zeroes.
So, if the square of a number ends with 10 zeroes, the number will have zeroes.
Is it possible for the square of a number to end with 5 zeroes ? Give reason.
Answer
According to the property of square numbers, if a number ends with n zeroes, its square ends with 2n zeroes.
2n will always be an even number.
Hence, it is not possible for a square of a number to end with 5 zeroes.
Give reason to show that none of the numbers given below is a perfect square.
(i) 2162
(ii) 6843
(iii) 9637
(iv) 6598
Answer
According to the property of square numbers, a number having 2, 3, 7 or 8 in its unit's place is never a perfect square.
∴ (i) 2162, (ii) 6843, (iii) 9637 and (iv) 6598 are not perfect square.
State, whether the square of the following numbers is even or odd ?
(i) 23
(ii) 54
(iii) 76
(iv) 75
Answer
(i) 23
Digit at ones place = 3
Square of 3 is 9.
So, digit at ones place of square number = 9
Hence, square of 23 is odd.
(ii) 54
Digit at ones place = 4
Square of 4 is 16.
So, digit at ones place of square number = 6
Hence, square of 54 is even.
(iii) 76
Digit at ones place = 6
Square of 6 is 36.
So, digit at ones place of square number = 6
Hence, square of 76 is even.
(iv) 75
Digit at ones place = 5
Square of 5 is 25.
So, digit at ones place of square number = 5
Hence, square of 54 is odd.
Give reason to show that none of the numbers 640, 81000 and 3600000 is a perfect square.
Answer
According to the property of square numbers, if a number ends with n zeroes, its square ends with 2n zeroes.
2n will always be an even number. The numbers 640, 81000 and 3600000 have 1, 3 and 5 zeroes respectively.
Hence, the numbers 640, 81000 and 3600000 are not a perfect square.
Evaluate:
372 - 362
Answer
According to the property of square numbers, for any natural number n,
Hence,
Evaluate:
852 - 842
Answer
According to the property of square numbers, for any natural number n,
Hence,
Evaluate:
1012 - 1002
Answer
According to the property of square numbers, for any natural number n,
Hence,
Without doing the actual addition, find the sum of:
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Answer
As we know that, the sum of first n odd natural numbers = n2.
Hence, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = 144.
Without doing the actual addition, find the sum of:
1 + 3 + 5 + 7 + 9 + ............... + 39 + 41
Answer
As we know that, the sum of first n odd natural numbers = n2.
Hence, 1 + 3 + 5 + 7 + 9 + ............... + 39 + 41 = 441.
Without doing the actual addition, find the sum of:
1 + 3 + 5 + 7 + 9 + ............... + 51 + 53
Answer
As we know that, the sum of first n odd natural numbers = n2.
Hence, 1 + 3 + 5 + 7 + 9 + ............... + 51 + 53 = 729.
Write three sets of Pythagorean triplets such that each set has numbers less than 30.
Answer
32 + 42 = 52
52 + 122 = 132
102 + 242 = 262
Hence, (3,4,5), (5,12,13) and (10,24,26) are three sets of Pythagorean triplets.
A Pythagorean triplet has one number equal to 6. The Pythagorean triplet are :
5, 6, 7
6, 7, 8
4, 6, 8
6, 8, 10
Answer
Hence, option 4 is the correct option.
The number of digits in the square root of 1210000 is :
2
4
3
5
Answer
Number of digits in = 4.
Hence, option 2 is the correct option.
The greatest 3-digit perfect square number is :
121
961
100
900
Answer
Hence, option 2 is the correct option.
The area of a square plot is 441 m2. Its perimeter is :
84 m2
84 m
21 m
21 m2
Answer
Area of square plot = l2
Perimeter of square plot = 4 x l
Hence, option 2 is the correct option.
Statement 1: 3675 is not a perfect square.
Statement 2: After grouping into pairs of equal factors of 3675, if we multiply or divide by the unpaired factor (if any) then the product or the quotient becomes a perfect square.
Which of the following options is correct ?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Finding prime factors of 3675, we get :
⇒ 3675 = 3 x (5 x 5) x (7 x 7)
Since the prime factor 3 is not in pair.
∴ 3675 is not a perfect square.
So, statement 1 is true.
⇒ 3675 = 3 x (5 x 5) x (7 x 7)
Multiplying by 3 on both sides, we get :
⇒ 3675 × 3 = (3 x 3) x (5 x 5) x (7 x 7)
⇒ 11025 = (3 x 3) x (5 x 5) x (7 x 7)
Since all prime factor are in pair. Therefore, 3675 x 3 is a perfect square.
⇒ 3675 = 3 x (5 x 5) x (7 x 7)
Dividing by 3 on both sides, we get :
⇒ = (5 x 5) x (7 x 7)
⇒ 1225 = (5 x 5) x (7 x 7)
Since all prime factor are in pair. Therefore, 3675 ÷ 3 is a perfect square.
So, statement 2 is true.
Hence, option 1 is the correct option.
Assertion (A) :
Reason (R) : The square root of a number n is that number which when multiplied by itself gives n as the product.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
We know that,
The square root of any number n is that number which when multiplied by itself gives n as the product.
⇒
So, reason (R) is true.
Solving,
So, assertion (A) is true and reason (R) clearly explains assertion.
Hence, option 1 is the correct option.
Assertion (A) : 49 is a perfect square, when divided by 3 remainder is 1.
Reason (R) : When each of the perfect square numbers 1, 4, 9, ............. is divided by 3, the remainder is always 1.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Finding prime factors of 49, we get :
⇒ 49 = (7 x 7)
Since all prime factors are in pair.
∴ 49 is a perfect square.
49 divided by 3 leaves quotient 16 and remainder 1.
⇒ 49 = 3 x 16 + 1
So, assertion (A) is true.
For each perfect squares,
1 divided by 3 leaves quotient 0 and remainder 1.
⇒ 1 = 3 x 0 + 1
4 divided by 3 leaves quotient 1 and remainder 1.
⇒ 4 = 3 x 1 + 1
16 divided by 3 leaves quotient 5 and remainder 1.
⇒ 16 = 3 x 5 + 1
25 divided by 3 leaves quotient 8 and remainder 1.
⇒ 25 = 3 x 8 + 1
36 divided by 3 leaves quotient 12 and remainder 0.
⇒ 36 = 3 x 12 + 0
Therefore when each of the perfect square numbers 1, 4, 9, ............. is divided by 3, the remainder is not always 1.
So, reason (R) is false.
Hence, option 3 is the correct option.
Assertion (A) : Natural numbers 5, 12 and 13 are Pythagorean triplets as 122 + 52 = 132.
Reason (R) : For any natural number n, (n + 1)2 - n2 = (n + 1) + n.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
According to assertion,
⇒ 122 + 52 = 132
Solving L.H.S. of the above equation, we get :
⇒ 122 + 52
⇒ 144 + 25
⇒ 169
⇒ 13 x 13
⇒ 132
Since, L.H.S. = R.H.S.
So, assertion (A) is true.
According to reason,
⇒ (n + 1)2 - n2 = (n + 1) + n.
Solving L.H.S. of the above equation, we get :
⇒ (n + 1)2 - n2
Using formula; a2 - b2 = (a - b)(a + b), we get :
= [(n + 1) - n][(n + 1) + n]
= [n + 1 - n][n + 1 + n]
= 1 x [(n + 1) + n]
= (n + 1) + n
Since, L.H.S. = R.H.S.
So, reason (R) is true but it does not explain assertion (A).
Hence, option 2 is the correct option.
Assertion (A) : 1 + 3 + 5 + 7 + ....... + 21 = 102.
Reason (R) : The sum of first n odd natural numbers = n2.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
We know that,
The sum of first n odd natural numbers = n2.
So, reason (R) is true.
According to assertion :
1 + 3 + 5 + 7 + ....... + 21 = 102
Solving the L.H.S. of above equation, we get :
⇒ 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
The above is a sum of the first 11 odd natural numbers. So, by formula
⇒ 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 = 112 = 121.
So, assertion (A) is false.
Hence, option 4 is the correct option.
Express 212 as the sum of two consecutive whole numbers.
Answer
Hence, the sum of 220 and 221 is equivalent to 212.
Find the square root of by prime factorisation method.
Answer
Hence,
Is 336 a perfect square ? If not, find the smallest multiple of 336 which is a perfect square.
Answer
Finding prime factors of 336
Since the prime factor 3 and 7 are not in pair.
Hence, 336 is not a perfect square. 21 should be multiplied with 336 so that the product is a perfect square.
Find the least number that must be subtracted from 980 so as to get a perfect square. Also, find the square root of the perfect number obtained.
Answer
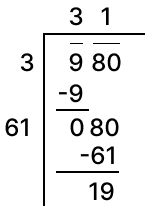
∴ If 19 is subtracted from 980, the resulting number will be a perfect square.
Hence, 19 should be subtracted from 980 and .
Find the smallest and the greatest 4-digit numbers, each of which is a perfect square.
Answer
The smallest 4-digit number = 1000
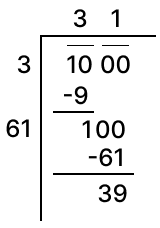
As we can see 1000 is not a perfect square.
Clearly, 1000 is greater than 312.
∴ On adding the required number to 1000, we shall be getting 322 i.e, 1024
So, the required number = 1024 -1000 = 24.
1000 + 24 = 1024 is a perfect square.
The greatest 4-digit number = 9999
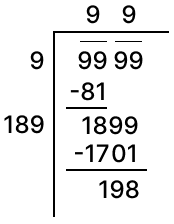
Clearly, 9999 is greater than 992.
∴ On subtracting the required number to 9999, we shall be getting 992 i.e, 9801.
So, the required number = 9999 - 198 = 9801.
Hence, 1024 and 9801 are the smallest and greatest 4-digit number.
Because = 43, find the value of :
(i) +
(ii) -
Answer
(i)
Hence,
(ii)
Hence,
The product of two numbers is 256. If one number is four times the other, find the numbers.
Answer
Let the first number be
The second number is four times the other =
Hence,
The numbers are 8 and 32.
The area of a square plot is 2116 m2. A man takes 5 rounds of the boundary of this plot, find the distance covered by him.
Answer
Area of square plot = l2
Perimeter of square plot = 4 x l
The man take 5 rounds = 5 x 184m = 920m.
Hence, the total distance travelled by the man = 920m.
Find the smallest square number which is divisible by 6, 9 and 15.
Answer
LCM of 6, 9 and 15 is 2 x 3 x 3 x 5 = 90
As 2 and 5 are not in pair. To make it a perfect square, it must be multiplied with 2 x 5 = 10.
∴ Required perfect square = 90 x 10 = 900.
The smallest square number which is divisible by 6, 9 and 15 is 900.