Special Types of Quadrilaterals

In the given figure ABCD is a parallelogram, angles DAB and ABC are in the ratio 5 : 7, the value of x is:

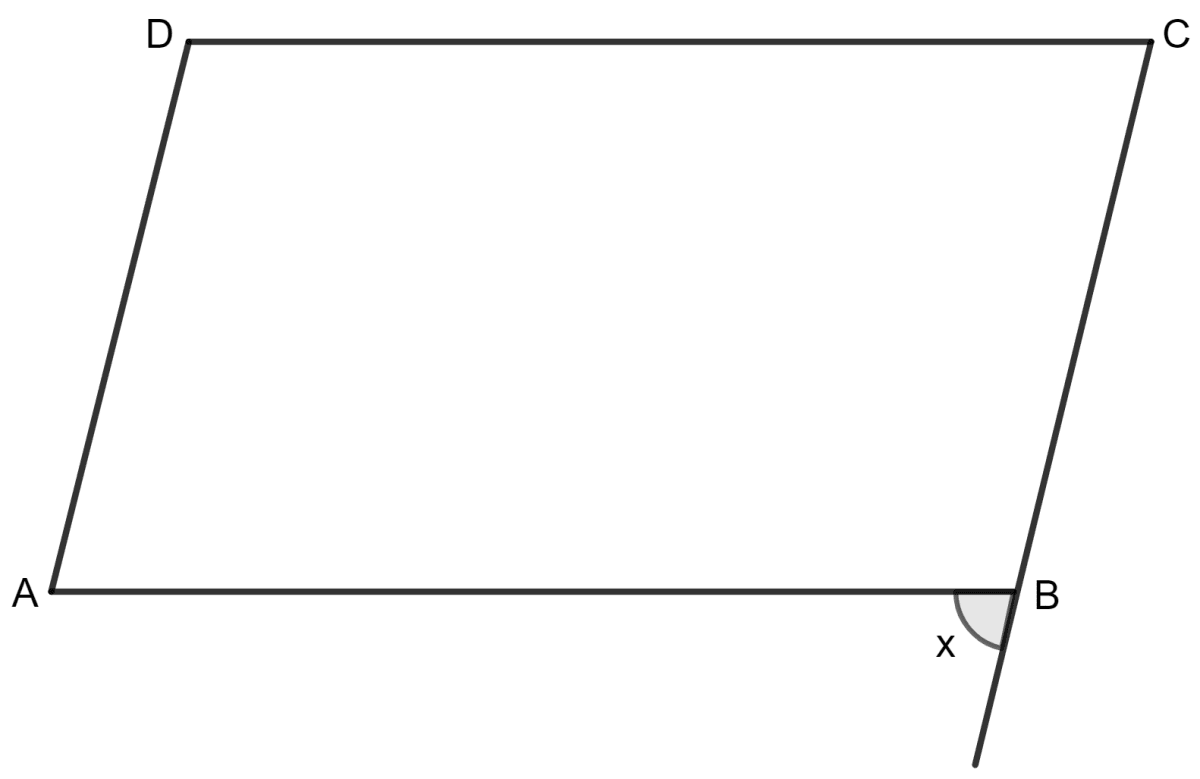
1. 105°

2. 85°

3. 75°

4. none of these

Answer

As we know that the consecutive angles of a parallelogram are supplementary.

Let ∠DAB = 5a and ∠ABC = 7a.

Since consecutive angles are supplementary:

⇒ ∠DAB + ∠ABC = 180°

⇒ 5a + 7a = 180°

⇒ 12a = 180°

⇒ a = $\dfrac{180°}{12}$

⇒ a = 15°

Then,

∠ABC = 7a = 7 $\times$ 15° = 105°

The other angle x,

x + ∠ABC = 180°

⇒ x + 105° = 180°

⇒ x = 180° - 105°

⇒ x = 75°

Hence, option 3 is the correct option.

ABCD is a rectangle. To make it a square which of the following condition(s) must be satisfied:

1. AC = BD

2. AC ⊥ BD

3. Diagonals bisect each other

4. AB = CD

Answer

In a rectangle ABCD, we know that AB = CD and BC = DA. Additionally, AB ⊥ BC and BC ⊥ CD.

For ABCD to be a square, its diagonals must be perpendicular to each other.

Hence, option 2 is the correct option.

In quadrilateral ABCD, AB//DC, then:

1. ∠A + ∠B = 180°

2. ∠A + ∠C = 180°

3. ∠C + ∠D = 180°

4. ∠A + ∠D = 180°

Answer

In quadrilateral ABCD, where AB//DC,

The consecutive angles between the parallel sides are supplementary.

Thus, ∠A + ∠D = 180°.

Hence, option 4 is the correct option.

The diagonals of a quadrilateral are equal and bisect each other. The quadrilateral is a :

1. square

2. rhombus

3. parallelogram

4. rectangle

Answer

A rectangle is a quadrilateral in which the diagonals are equal in length and bisect each other.

Hence, option 4 is the correct option.

A quadrilateral will be a square, if its:

1. each angle is 90°

2. each angle is 90° and the diagonals are equal

3. all the sides are equal

4. all the sides are equal and each angle is 90°

Answer

A quadrilateral will be a square if:

• All the sides are equal ,

• Each angle is right angle,

• Diagonals are equal, and

• Diagonals intersect at right angle.

Hence, option 4 is the correct option.

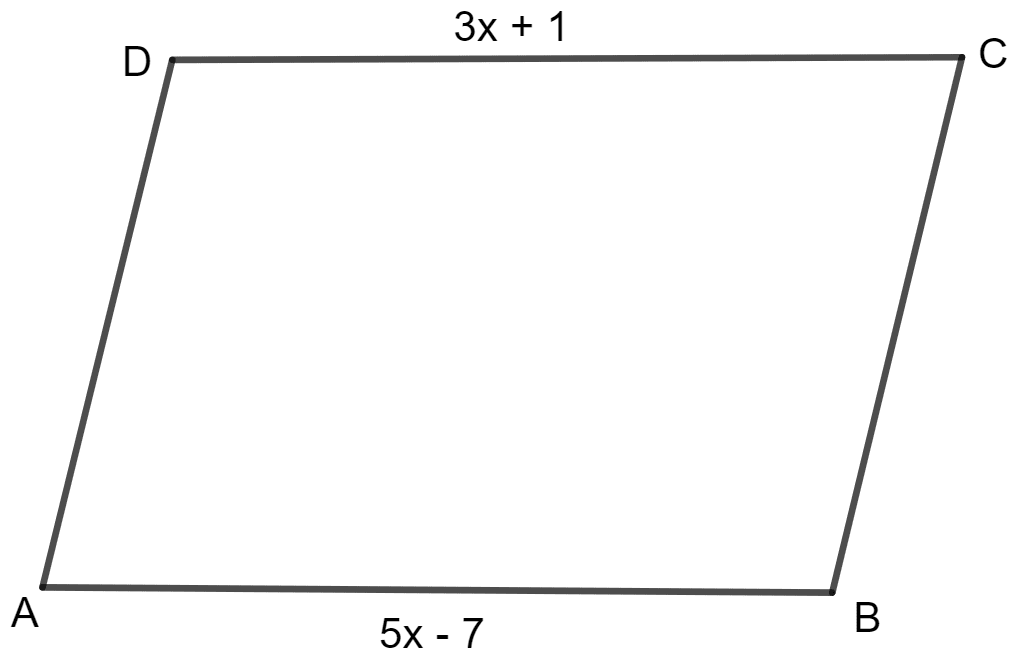
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x - 7 and CD = 3x + 1, find the length of CD.

Answer

It is given that in parallelogram ABCD, ∠A = 3 times ∠B.

Let ∠B be a.

Then, ∠A = 3a.

As we know, the consecutive angles of a parallelogram are supplementary.

⇒ ∠A + ∠B = 180°

⇒ 3a + a = 180°

⇒ 4a = 180°

⇒ a = $\dfrac{180°}{4}$

⇒ a = 45°

Thus, ∠B = ∠D = a = 45°.

And, ∠A = ∠C = 3a = 3 $\times$ 45° = 135°

It is also given that AB = 5x - 7 and CD = 3x + 1.

AB = CD (opposite sides of parallelogram are equal)

⇒ (5x - 7) = (3x + 1)

⇒ 5x - 7 = 3x + 1

⇒ 5x - 3x = 7 + 1

⇒ 2x = 8

⇒ x = $\dfrac{8}{2}$

⇒ x = 4

CD = 3x + 1

= 3 $\times$ 4 + 1

= 12 + 1

= 13

Hence, ∠A = 135°, ∠C = 135°, ∠B = 45°, ∠D = 45° and CD = 13 units.

In parallelogram PQRS, ∠Q = (4x - 5)° and ∠S = (3x + 10)°. Calculate: ∠Q and ∠R.

Answer

It is given that in parallelogram PQRS, ∠Q = (4x - 5)° and ∠S = (3x + 10)°.

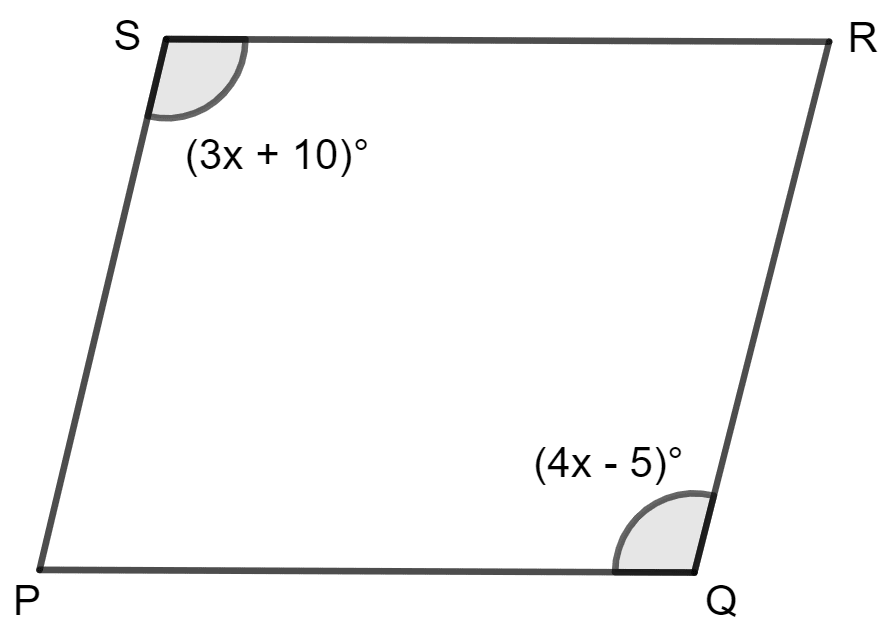
In a parallelogram, opposite angles are equal, so:

∠Q = ∠S and ∠R = ∠P.

Therefore,

⇒ (4x - 5)° = (3x + 10)°

⇒ 4x° - 5° = 3x° + 10°

⇒ 4x° - 3x° = 5° + 10°

⇒ 1x° = 15°

So, ∠Q = (4x - 5)°

= (4 $\times$ 15 - 5)°

= (60 - 5)°

= 55°

As we know, the consecutive angles of a parallelogram are supplementary.

⇒ ∠Q + ∠R = 180°

⇒ 55° + ∠R = 180°

⇒ ∠R = 180° - 55°

⇒ ∠R = 125°

Hence, ∠Q = 55° and ∠R = 125°.

In rhombus ABCD :

(i) if ∠A = 74°, find ∠B and ∠C.

(ii) if AD = 7.5 cm, find BC and CD.

Answer

(i) In a rhombus, opposite angles are equal, and the diagonals bisect each other at 90°. Additionally, consecutive angles are supplementary.

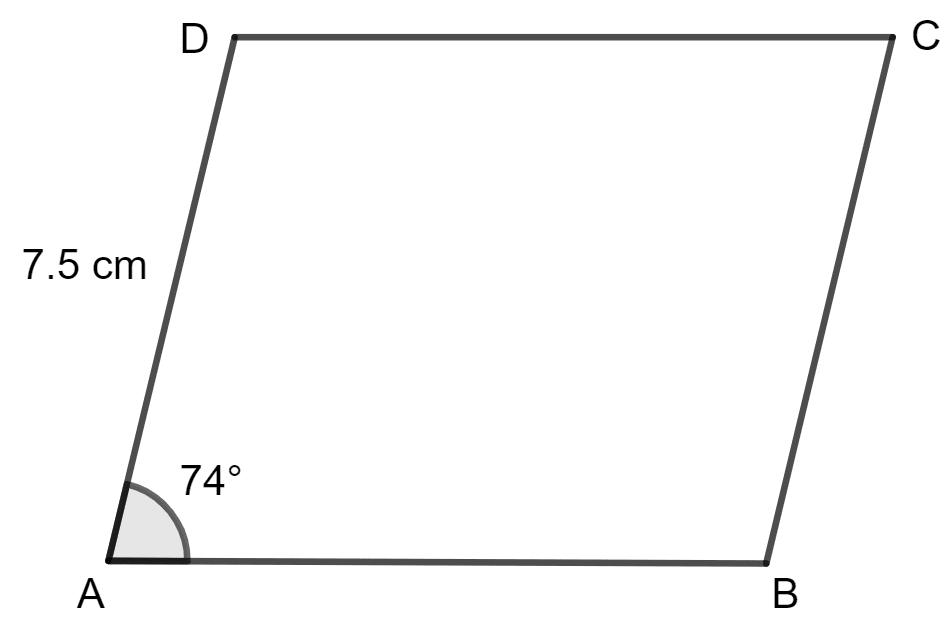
⇒ ∠A + ∠B = 180°

It is given that ∠A = 74°.

⇒ 74° + ∠B = 180°

⇒ ∠B = 180° - 74°

⇒ ∠B = 106°

Since opposite angles are equal, we have:

∠A = ∠C and ∠B = ∠D

Hence, ∠B = 106° and ∠C = 74°.

(ii) In a rhombus, all sides are equal.

Therefore, AB = BC = CD = DA = 7.5 cm.

Hence, the length of sides BC = CD = 7.5cm.

In square PQRS :

(i) if PQ = 3x - 7 and QR = x + 3, find PS.

(ii) if PR = 5x and QS = 9x — 8. Find QS.

Answer

(i) In a square PQRS, all sides are equal and all angles are 90°.

Thus, PQ = QR = PS = RS.

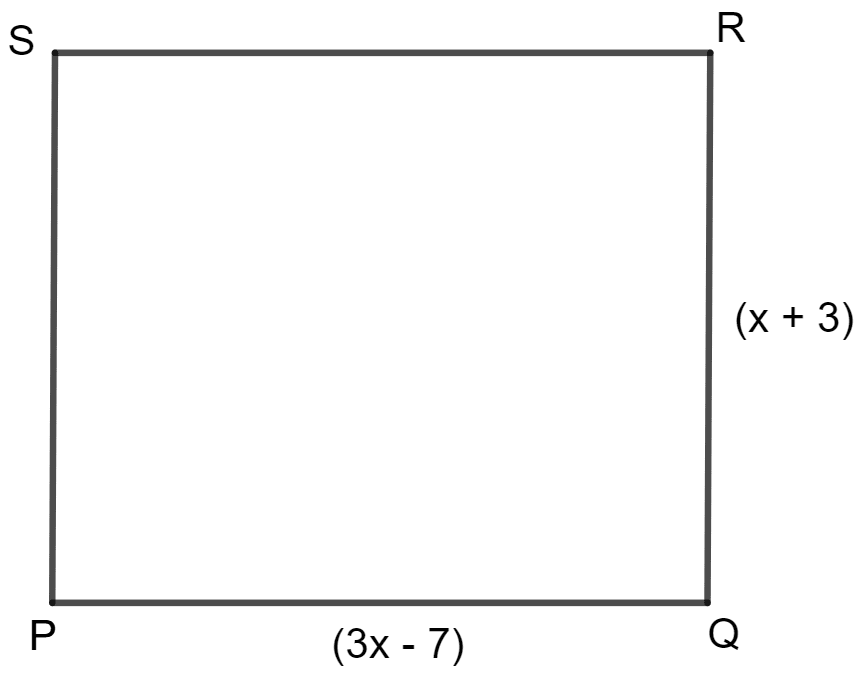
It is given that PQ = 3x - 7 and QR = x + 3.

⇒ (3x - 7) = (x + 3)

⇒ 3x - 7 = x + 3

⇒ 3x - x = 7 + 3

⇒ 2x = 10

⇒ x = $\dfrac{10}{2}$

⇒ x = 5

Now, substitute the value of x = 5 into the expression for PQ:

PQ = QR = PS = RS = (3x - 7)

= (3 $\times$ 5 - 7)

= (15 - 7)

= 8

Hence, the length of PS = 8 units.

(ii) In a square PQRS, all sides are equal and all angles are 90°.

Thus, PQ = QR = PS = RS.

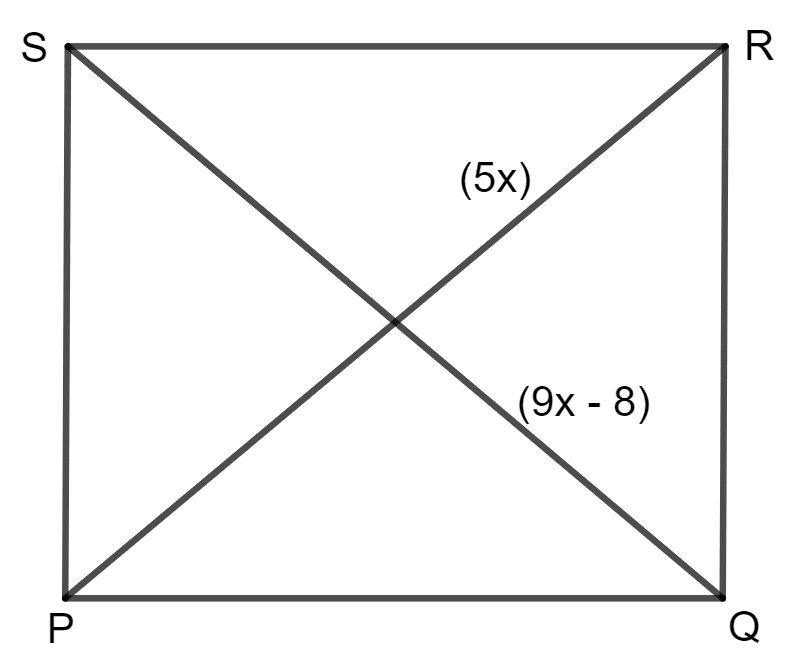
It is given that PR = 5x and QS = 9x - 8.

⇒ (5x) = (9x - 8)

⇒ 5x = 9x - 8

⇒ 9x - 5x = 8

⇒ 4x = 8

⇒ x = $\dfrac{8}{4}$

⇒ x = 2

Now, substitute the value of x = 2 into the expression for PQ:

PQ = QR = PS = RS = 5x

= 5 $\times$ 2

= 10

Hence, the length of QS = 10 units.

ABCD is a rectangle. If ∠BPC = 124°, calculate :

(i) ∠BAP

(ii) ∠ADP.

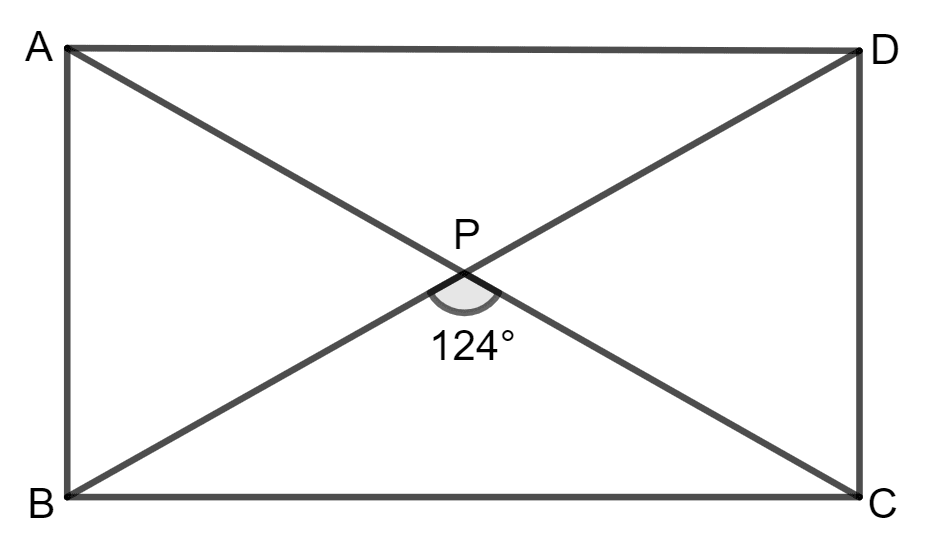
Answer

Since ABCD is a rectangle, the diagonals bisect each other, and ∠BPC forms two angles at point P.

According to the properties of a rectangle, the diagonals are equal and intersect at the midpoint.

(i) ∠BAP = $\dfrac{1}{2}$ of ∠BPC (since diagonals bisect each other).

So, ∠BAP = $\dfrac{1}{2}$ × 124° = 62°.

Hence, the value of ∠BAP is 62°.

(ii) Diagonals of rectangle are equal and bisect each other.

⇒ ∠PBC = ∠PCB = x (say)

But, in triangle BPC, sum of all the angles are 180°.

⇒ ∠BPC + ∠PBC + ∠PCB = 180°

⇒ 124° + x + x = 180°

⇒ 2x = 180° − 124°

⇒ 2x = 56°

⇒ x = 28°

⇒ ∠PBC = 28°

But ∠PBC = ∠ADP [alternate angles]

∠ADP = 28°

Hence, the value of ∠ADP is 28°.

ABCD is a rhombus. If ∠BAC = 38°, find :

(i) ∠ACB

(ii) ∠DAC

(iii) ∠ADC.

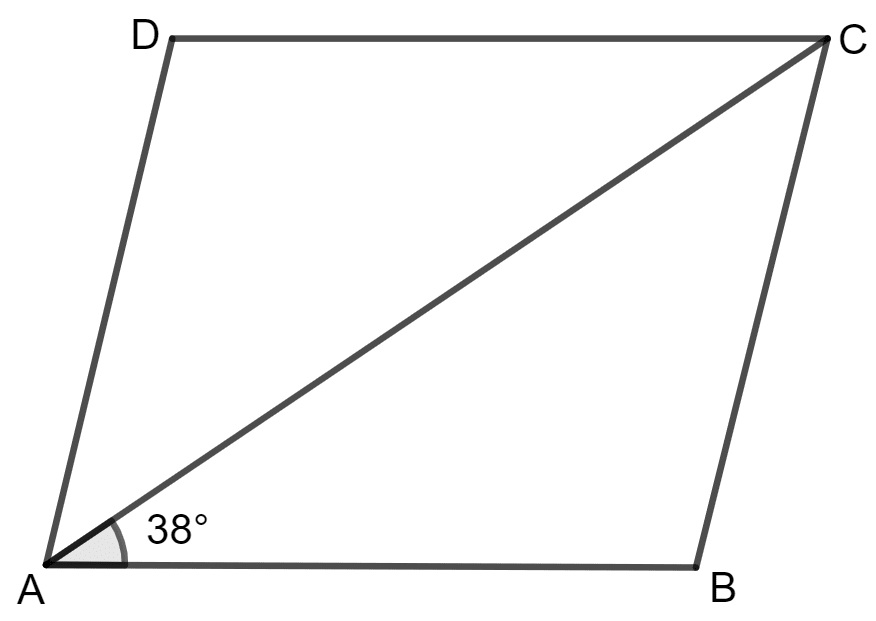
Answer

(i) In a rhombus, all sides are equal.

⇒ AB = BC = CD = DA

And, opposite angles of a rhombus are equal.

∠BAC = ∠ACB

It is given that ∠BAC = 38°.

So, ∠ACB = ∠BAC = 38°.

Hence, the value of ∠ACB is 38°.

(ii) Since ABC is a triangle, the sum of angles in a triangle is 180°.

Therefore,

⇒ ∠ABC + ∠BAC + ∠ACB = 180°

⇒ ∠ABC + 38° + 38° = 180°

⇒ ∠ABC + 76° = 180°

⇒ ∠ABC = 180° - 76°

⇒ ∠ABC = 104°

Since opposite angles of a rhombus are equal:

⇒ ∠ABC = ∠ADC

⇒ ∠ADC = 104°

As AD = CD, we have:

∠DAC = ∠DCA

Now,

⇒ ∠DAC = $\dfrac{1}{2}$ [180° - 104°]

= $\dfrac{1}{2}$ [76°]

= 38°

Hence, the value of ∠DAC is 38°.

(iii) Since opposite angles of a rhombus are equal:

⇒ ∠ABC = ∠ADC

⇒ ∠ADC = 104°

Hence, the value of ∠ADC is 104°.

ABCD is a rhombus. If ∠BCA = 35°, find ∠ADC.

Answer

In rhombus ABCD, all sides are equal:

AB = BC = CD = DA

Thus, alternate angles are equal:

∠DAC = ∠BCA

It is given that ∠BCA = 35°.

⇒ ∠DAC = ∠BCA = 35°

And, ∠DAC = ∠ACD [as AD = CD]

⇒ 35° = ∠ACD

In triangle ADC, sum of all the angles of triangles is 180°

⇒ ∠DAC + ∠ACD + ∠ADC = 180°

⇒ 35° + 35° + ∠ADC = 180°

⇒ 70° + ∠ADC = 180°

⇒ ∠ADC = 180° - 70°

⇒ ∠ADC = 110°

Hence, the value of ∠ADC is 110°.

PQRS is a parallelogram whose diagonals intersect at M.

If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°, find :

(i) ∠RPS

(ii) ∠PRS

(iii) ∠PSR.

Answer

(i) PQRS is a parallelogram which means opposite sides are parallel.

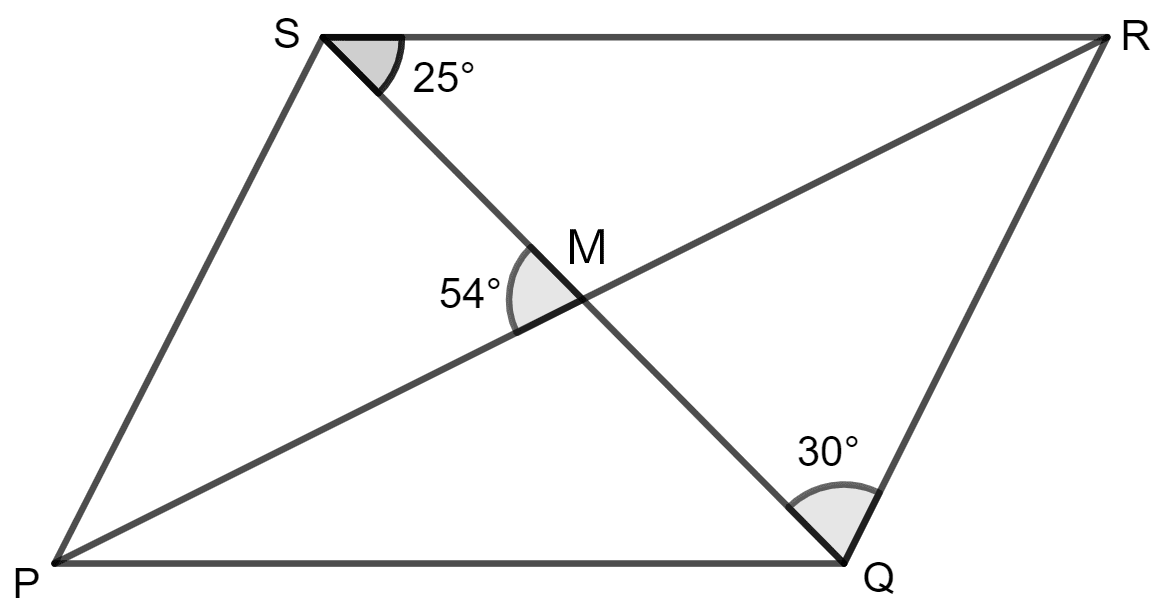
When QR is parallel to PS.

⇒ ∠PSQ = ∠SQR (alternate angles)

It is given that ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°

So, ∠PSQ = ∠SQR = 30°

In triangle SMP, sum of all the angles of triangle is = 180°

⇒ ∠PMS + ∠PSM + ∠MPS = 180°

(As we know , ∠MPS = ∠RPS)

⇒ 54° + 30° + ∠RPS = 180°

⇒ 84° + ∠RPS = 180°

⇒ ∠RPS = 180° - 84°

⇒ ∠RPS = 96°

Hence, the value of ∠RPS is 96°.

(ii) Now, consider triangle MSR, according to exterior angle property, exterior angle is equals to sum of two opposite interior angles.

∠MRS + ∠RSM = ∠PMS

⇒ ∠PRS + 25° = 54°

⇒ ∠PRS = 54° - 25°

⇒ ∠PRS = 29°

Hence, the value of ∠PRS is 29°.

(iii) ∠PSR is divided into two angles ∠PSQ and ∠RSQ. So,

∠PSR = ∠PSQ + ∠RSQ

= 30° + 25°

= 55°

Hence, the value of ∠PSR is 55°.

Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.

Prove : M is the mid-point of LN.

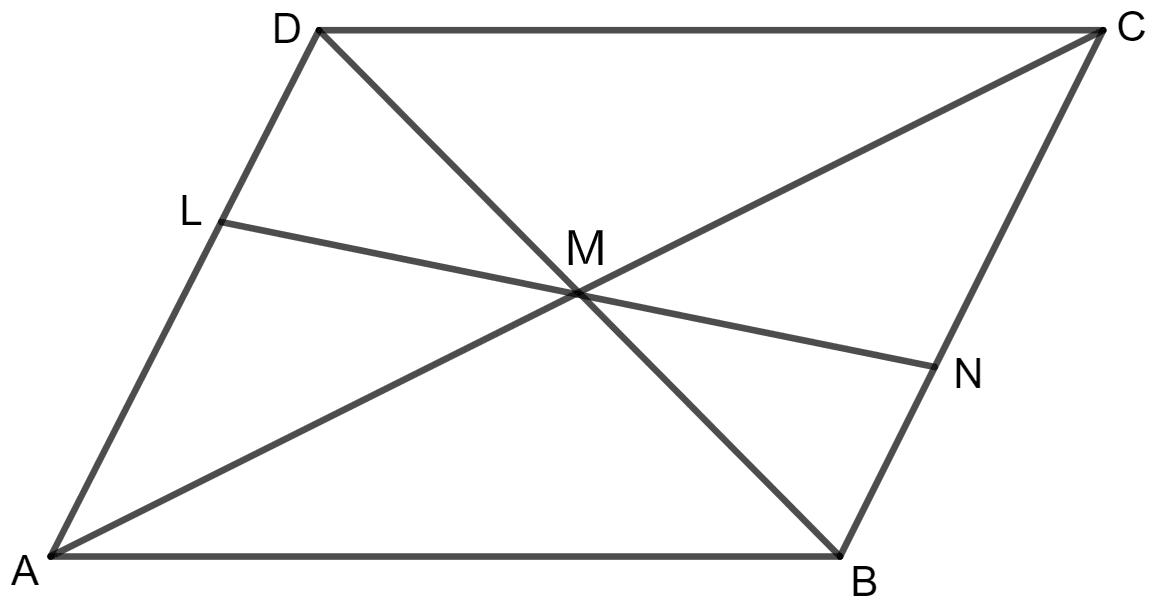
Answer

According to the properties of a parallelogram, the diagonals of a parallelogram bisect each other.

⇒ MD = MB

Also, ∠ADB = ∠DBN (∵ alternate angles)

And, ∠DML = ∠BMN (∵ vertically opposite angles)

Hence, by Angle Side Angle congruency,

Δ DML ≅ Δ BMN

By using Corresponding Parts of Congruent Triangles,

LM = MN

∵ M is mid - point of LN.

Hence, M is the mid-point of LN

In an isosceles-trapezium, show that the opposite angles are supplementary.

Answer

ABCD is an isosceles trapezium in which AD = BC.

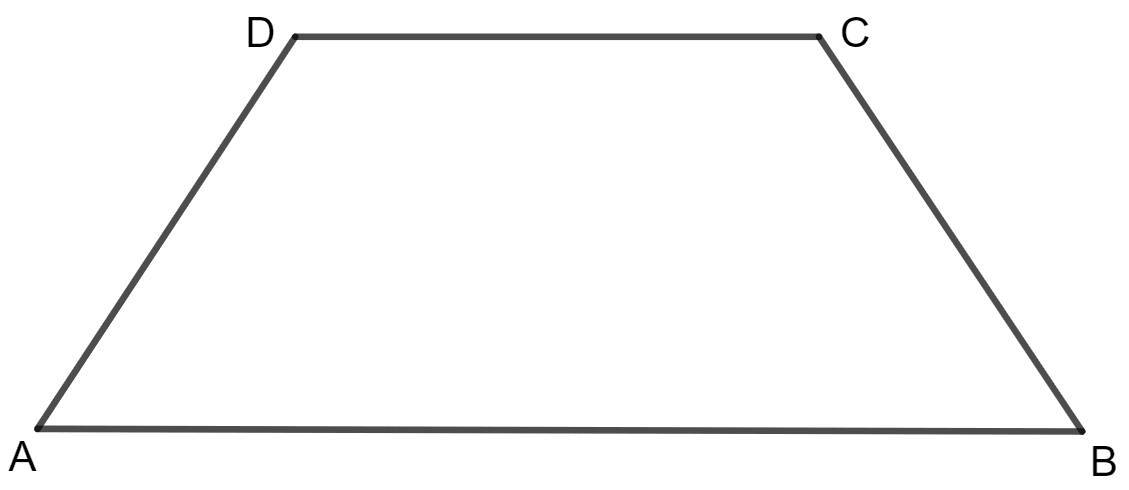
To prove:

∠ A + ∠ C = 180°

and, ∠ B + ∠ D = 180°

Proof:

AB is parallel to CD. So, sum of adjacent angles is 180°.

⇒ ∠ A + ∠ D = 180°

It is already given that ABCD is an isosceles trapezium which means AD = BC.

⇒ ∠ A = ∠ B

So,

⇒ ∠ B + ∠ D = 180°

In a trapezium, sum of all angles is always equal to 360°.

⇒ ∠ A + ∠ B + ∠ C + ∠ D = 360°

⇒ ∠ A + ∠ C + (∠ B + ∠ D) = 360°

⇒ ∠ A + ∠ C + 180° = 360°

⇒ ∠ A + ∠ C = 360° - 180°

⇒ ∠ A + ∠ C = 180°

Hence, the opposite angles are supplementary.

ABCD is a parallelogram. What kind of quadrilateral is it if :

(i) AC = BD and AC is perpendicular to BD ?

(ii) AC is perpendicular to BD but is not equal to it ?

(iii) AC = BD but AC is not perpendicular to BD?

Answer

(i) It is given that AC = BD and AC is perpendicular to BD.

That is, the diagonals of the parallelogram are equal and perpendicular to each other.

Hence, the parallelogram is a square.

(ii) It is given that AC is perpendicular to BD but is not equal to it.

That is, the diagonals of the parallelogram are perpendicular to each other but not equal to each other.

Hence, the parallelogram is a rhombus.

(iii) It is given that AC = BD but AC is not perpendicular to BD.

That is, the diagonals of the parallelogram are equal but not perpendicular.

Hence, the parallelogram is a rectangle.

Prove that the diagonals of a parallelogram bisect each other.

Answer

Given:

ABCD is an parallelogram.

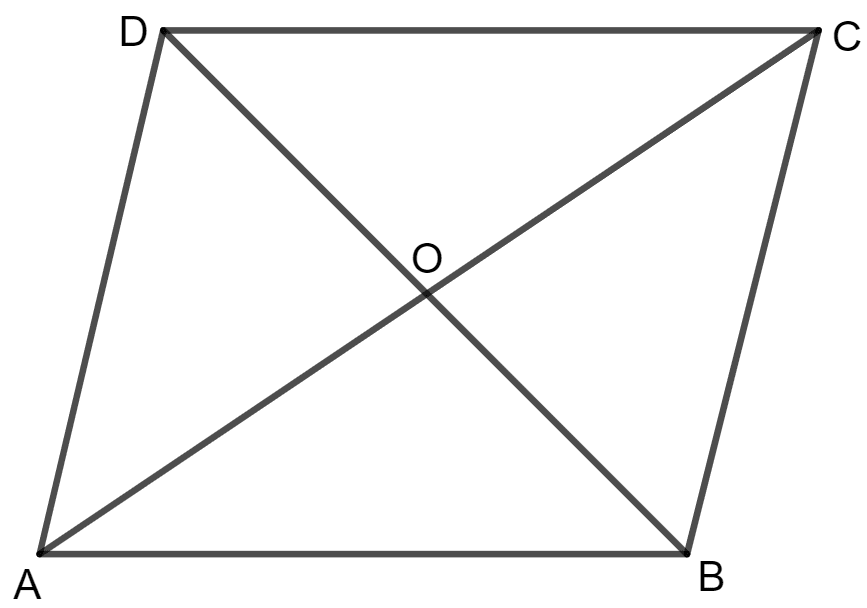
To prove:

OA = OC and OB = OD

Proof:

As ABCD is a parallelogram which means AB is parallel to CD.

In Δ OCD and Δ OAB

∠ OBA = ∠ ODC (alternate angles)

∠ OAB = ∠ OCD (alternate angles)

AB = CD (opposite side of parallelogram)

By Angle side angle congruency

Δ OCD ≅ Δ OAB

By using Corresponding parts of congruent triangles,

OA = OC and OB = OD

Hence, the diagonals of a parallelogram bisect each other.

If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.

Answer

Given:

A parallelogram ABCD with diagonals AC and BD of equal lengths.

To prove:

The parallelogram ABCD is a rectangle.

Proof:

Consider triangles Δ ABC and Δ ABD:

• AB = AB (Common side)

• AC = BD (Given)

• BC = AD (opposite sides of parallelogram)

By Side Side Side congruency,

Δ ABC ≅ Δ ABD

By using Corresponding Parts of Congruent Triangles,

∠ A = ∠ B

But we know that adjacent angles of parallelogram are supplementary.

∠ A + ∠ B = 180°

∠ A = ∠ B = 90°

Similarly, ∠ C = ∠ D = 90°

Hence, if the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle.

In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.

Answer

Given:

Parallelogram ABCD in which E and F are mid - points of AD and BC.

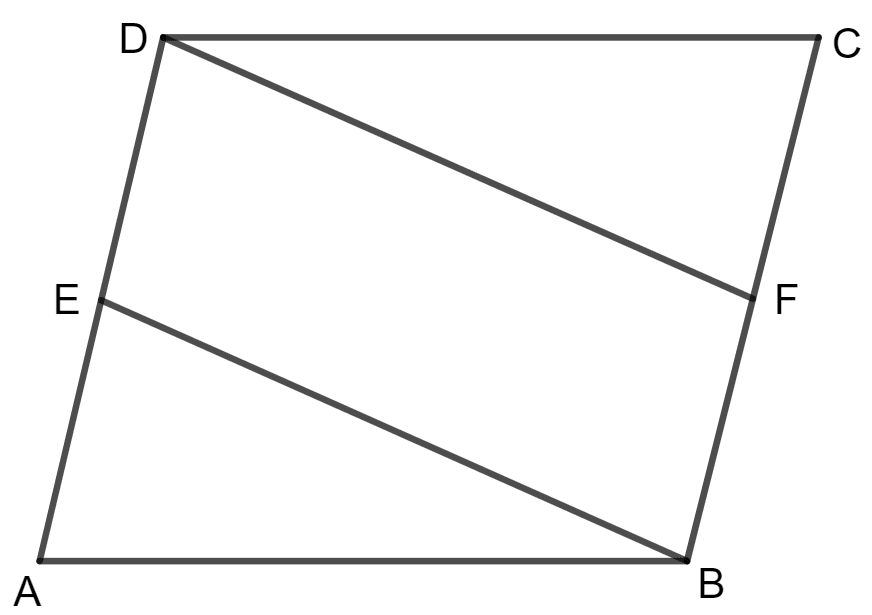
To prove:

BFDE is a parallelogram

Proof:

E is the mid-point of AD.

DE = $\dfrac{1}{2}$ AD

Also, F is the mid-point of BC.

BF = $\dfrac{1}{2}$ BC

But as we know opposite sides of parallelogram are equal.

So, AD = BC

Therefore, DE = BF

And, also AD is parallel to BC.

So, DE is parallel to BF.

When DE = BF and DE is parallel to BF. (opposite sides are equal and parallel to each other)

Hence, BFDE is a parallelogram.

The given figure shows a parallelogram. The value of x for which it will be a rhombus is :

1. 35°

2. 25°

3. 15°

4. 45°

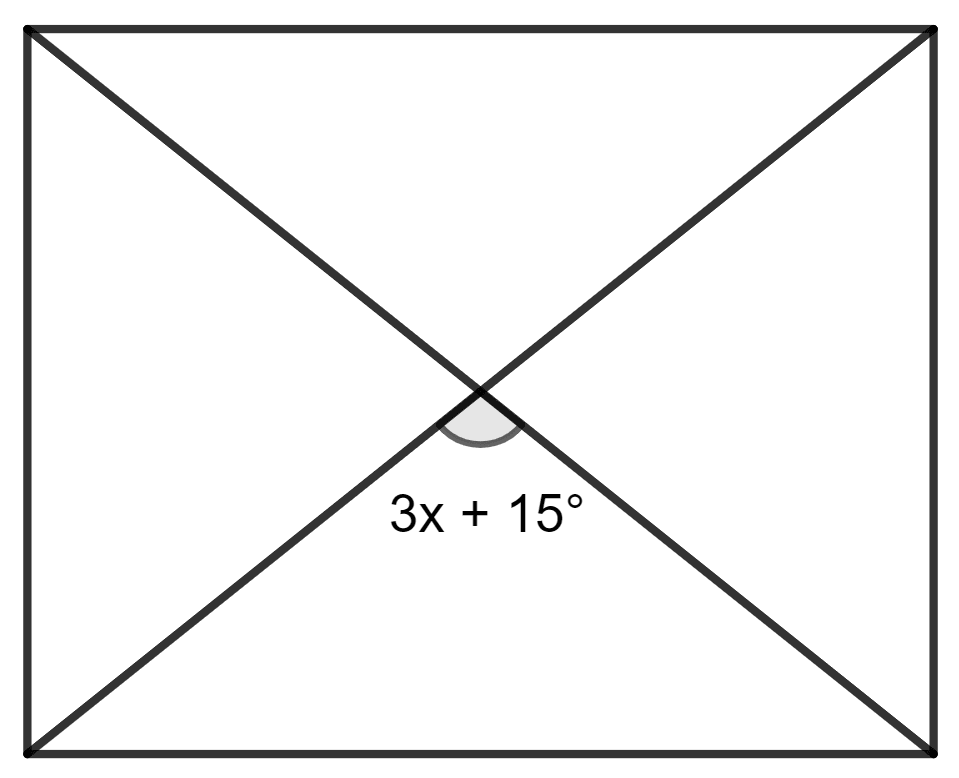
Answer

Using the property, a parallelogram whose diagonals intersect at 90° is a rhombus.

So, 3x + 15° = 90°

⇒ 3x = 90° - 15°

⇒ 3x = 75°

⇒ x = $\dfrac{75°}{3}$

⇒ x = 25°

Hence, option 2 is the correct option.

A rhombus will be a square, if :

1. its diagonals bisect each other

2. its diagonals are perpendicular to each other

3. one of its angles is 60°

4. none of these

Answer

A rhombus will be a square if each angle is 90° and diagonals are equal.

Hence, option 4 is the correct option.

The diagonals of a quadrilateral, bisect each other at right-angle. The quadrilateral is a:

1. trapezium

2. square

3. rhombus

4. parallelogram

Answer

A quadrilateral whose diagonals intersect at 90° is a rhombus.

Hence, option 3 is the correct option.

In a parallelogram ABCD; ∠A = (3x + 2)° and ∠D = (2x + 3)°; the value of x is :

1. 37

2. 35

3. 30

4. 40

Answer

According to the properties of parallelogram, consecutive angles of a parallelogram are supplementary.

⇒ ∠ A + ∠ D = 180°

⇒ (3x + 2)° + (2x + 3)° = 180°

⇒ 3x° + 2° + 2x° + 3° = 180°

⇒ 5x° + 5° = 180°

⇒ 5x° = 180° - 5°

⇒ 5x° = 175°

⇒ x° = $\dfrac{175°}{5}$

⇒ x° = 35°

Hence, option 2 is the correct option.

In a trapezium ABCD, AB//DC and AD = BC. If ∠A = (5x + 8)° and ∠D = (4x + 10)°; the measure of angle B is

1. 98°

2. 82°

3. 96°

4. none of these

Answer

According to the properties of parallelogram, consecutive angles of a parallelogram are supplementary.

⇒ ∠ A + ∠ D = 180°

⇒ (5x + 8)° + (4x + 10)° = 180°

⇒ 5x° + 8° + 4x° + 10° = 180°

⇒ 9x° + 18° = 180°

⇒ 9x° = 180° - 18°

⇒ 9x° = 162°

⇒ x° = $\dfrac{162°}{9}$

⇒ x° = 18°

So, ∠ A = (5x + 8)°

= (5 $\times$ 18 + 8)°

= (90 + 8)°

= 98°

It is given that AD = BC. Therefore, ∠ A = ∠ B

⇒ ∠ B = 98°

Hence, option 1 is the correct option.

Statement 1: In order to prove that a given parallelogram is a rectangle, we must prove that (a) any angle of it is 90° or (b) its diagonal are equal.

Statement 2: A kite is an arrowhead in which two pairs of adjacent sides are equal.

Which of the following options is correct?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

A given parallelogram is a rectangle;

If one angle of a parallelogram is 90°, then all angles must be 90° due to the properties of parallelograms (opposite angles are equal, and adjacent angles are supplementary). Therefore, the parallelogram is a rectangle.

If the diagonals of parallelogram are equal, then it is a rectangle.

So, statement 1 is true.

A kite is a quadrilateral with two pairs of adjacent sides that are equal in length.

An arrowhead shape typically refers to a concave quadrilateral, which is not a standard definition of a kite.

So, statement 2 is false.

∴ Statement 1 is true, and statement 2 is false.

Hence, option 3 is the correct option.

Assertion (A) : In a parallelogram, the bisectors of any two pair of adjacent angles meet at right angle.

Reason (R) : In a parallelogram opposite angles are equal.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.

Answer

Let ABCD be the parallelogram. AO and BO be the bisector of angles A and B respectively.

∴ ∠BAO = $\dfrac{∠A}{2}$ and ∠ABO = $\dfrac{∠B}{2}$

We know that in a parallelogram, consecutive angles are supplementary.

⇒ ∠A + ∠B = 180°

⇒ $\dfrac{1}{2}$ (∠A + ∠B) = $\dfrac{1}{2}$ x 180°

⇒ $\dfrac{1}{2} ∠A + \dfrac{1}{2} ∠B$ = 90°

In ΔAOB, according to angle sum property

⇒ ∠AOB + ∠ABO + ∠BAO = 180°

⇒ ∠AOB + $\dfrac{1}{2}∠B + \dfrac{1}{2}∠A$ = 180°

⇒ ∠AOB + 90° = 180°

⇒ ∠AOB = 180° - 90°

⇒ ∠AOB = 90°

Thus, the bisector of any two pair of adjacent angles meet at right angle.

So, assertion (A) is true.

We know that,

The opposite angles of a parallelogram are equal.

∴ Reason (R) is true.

∴ Both A and R are correct, and R is not the correct explanation for A.

Hence, option 2 is the correct option.

Assertion (A) : One of the diagonals of rhombus is equals to one of its side. The angles of a rhombus are 60°, 120°, 60°, 120°.

Reason (R) : All the sides of a rhombus are equal.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.

Answer

By property,

All the sides of a rhombus are equal.

So, reason (R) is true.

ABCD is the rhombus and AC is the diagonal such that AC = AB.

In triangle ABC,

⇒ AB = BC (Sides of rhombus are equal)

⇒ AB = AC (Given)

⇒ AB = AC = BC

So, triangle ABC is an equilateral triangle.

∴ ∠B = 60°, ∠BAC = 60° and ∠BCA = 60°.

In triangle ADC,

⇒ AD = CD (Sides of rhombus are equal)

⇒ AD = AC (Since, AB = AC and AB = AD)

⇒ AD = CD = AC

So, triangle ADC is an equilateral triangle.

∴ ∠D = 60°, ∠DAC = 60° and ∠DCA = 60°

⇒ ∠A = ∠BAC + ∠DAC = 60° + 60° = 120°.

⇒ ∠C = ∠BCA + ∠DCA = 60° + 60° = 120°.

Hence, the angles of a rhombus are 60°, 120°, 60°, 120°.

So, assertion (A) is true.

∴ Both A and R are correct, and R is not the correct explanation for A.

Hence, option 2 is the correct option.

Assertion (A) : If one angle of a parallelogram measures 90°, the parallelogram is rectangle.

Reason (R) : If each interior angle of parallelogram is 90°, then all sides of it are equal.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.

Answer

If one angle is 90°, the opposite angle is also 90° as opposite angles of a parallelogram are equal.

If one angle is 90°, the adjacent angle is 180° - 90° = 90°, as the sum of adjacent angles in a rectangle is 180°.

Thus, all angles of parallelogram are 90° if one angle is 90°.

Therefore, the parallelogram is a rectangle.

So, assertion (A) is true.

A parallelogram with all interior angles equal to 90° is a rectangle, but not necessarily a square. Therefore, all sides are not necessarily equal.

So, reason (R) is false.

∴ A is true, but R is false.

Hence, option 3 is the correct option.

Assertion (A) : The adjacent angles of a parallelograms are in ratio 2 : 3 the remaining angles are 78° and 102°.

Reason (R) : Opposite angles of a parallelogram are equal.

1. Both A and R are correct, and R is the correct explanation for A.

2. Both A and R are correct, and R is not the correct explanation for A.

3. A is true, but R is false.

4. A is false, but R is true.

Answer

Given, the adjacent angles of a parallelograms are in ratio 2 : 3.

Let the adjacent angles be 2x and 3x.

We know that in a parallelogram, adjacent angles are supplementary.

⇒ 2x + 3x = 180°

⇒ 5x = 180°

⇒ x = $\dfrac{180°}{5}$

⇒ x = 36°

Adjacent angles = 2x = 2 x 36° = 72°

and, 3x = 3 x 36° = 108°.

Opposite angles of parallelogram are equal.

So, all angles of parallelogram are 78°, 108°, 78°, 108°.

So, assertion (A) is true.

By property,

Opposite angles of parallelogram are equal.

So, reason (R) is true.

∴ Both A and R are correct, and R is the correct explanation for A.

Hence, option 1 is the correct option.

The adjacent sides of a parallelogram are in the ratio 5 : 4. If the perimeter of the parallelogram is 108 cm, find the length of its sides.

Answer

The adjacent sides of a parallelogram are in the ratio 5 : 4.

And, the perimeter of the parallelogram is 108 cm.

As we know opposite sides of a parallelogram are equal.

Let the length of AB = CD = 5a

And, the length of BC = DA = 4a

Perimeter of parallelogram = sum of all length of sides.

⇒ 5a + 4a + 5a + 4a = 108 cm

⇒ 18a = 108 cm

⇒ a = $\dfrac{108}{18}$ cm

⇒ a = 6 cm

So, the length of AB = CD = 5a

= 5 x 6 cm

= 30 cm

And, the length of BC = DA = 4a

= 4 x 6 cm

= 24 cm

Hence, the lengths of all the sides are 30 cm, 24 cm, 30 cm, and 24 cm.

In the given figure, ABCD is a parallelogram. If OA = 6 cm and AC - BD = 2 cm; find the length of BD.

Answer

In a parallelogram, diagonal always bisect each other.

So, OA = $\dfrac{1}{2}$ AC

⇒ AC = 2 times OA

⇒ AC = 2 x 6 cm

⇒ AC = 12 cm

It is given that AC - BD = 2 cm

⇒ 12 - BD = 2

⇒ BD = 12 - 2

⇒ BD = 10

Hence, the length of BD is 10 cm.

The diagonals of a parallelogram ABCD intersect each other at point O. If OA = x + y, OC = 20, OD = x + 3 and OB = 18; find the values of x and y.

Answer

As per the properties of parallelogram, diagonal always bisect each other.

So, OB = OD

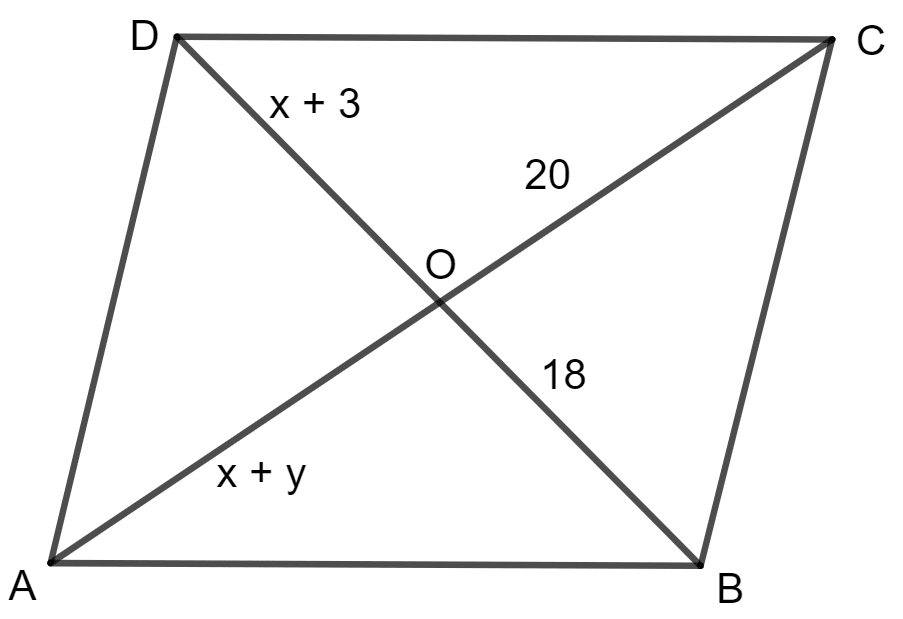
⇒ x + 3 = 18

⇒ x = 18 - 3

⇒ x = 15

And, OA = OC

⇒ x + y = 20

Putting x = 15

⇒ 15 + y = 20

⇒ y = 20 - 15

⇒ y = 5

Hence, the value of x = 15 and y = 5.

One of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.

Answer

One of the diagonals of a rhombus and its sides are equal.

ABCD is the rhombus and AC is the diagonal such that AC = AB.

In triangle ABC,

AB = BC (Sides of rhombus)

AB = AC (Given)

⇒ AB = AC = BC

So, triangle ABC is a equilateral triangle.

Therefore, ∠ B = 60°, ∠ BAC = 60° and ∠ BCA = 60°.

Similarly, triangle ADC is a equilateral triangle.

Therefore, ∠ D = 60°, ∠ DAC = 60° and ∠ DCA = 60°

∠ A = ∠ BAC + ∠ DAC

= 60° + 60°

= 120°

∠ C = ∠ BCA + ∠ DCA

= 60° + 60°

= 120°

Hence, the value of ∠ A = 120°, ∠ B = 60°, ∠ C = 120° and ∠ D = 60°.

In a parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :

(i) AE = AD

(ii) DE bisects ∠ADC and

(iii) Angle DEC is a right angle.

Answer

(i) Given:

Parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD.

To prove:

AE = AD

Proof:

Firstly join DE.

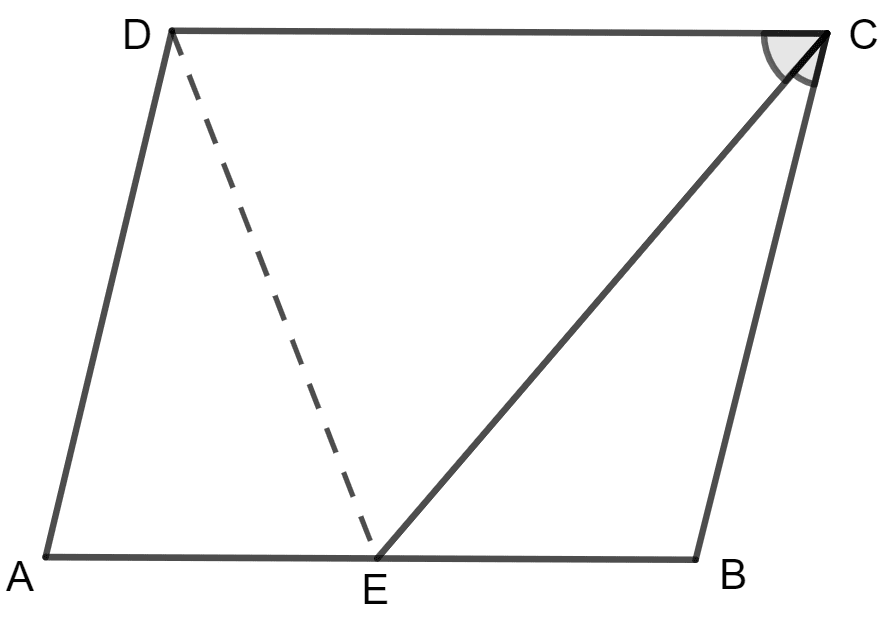
It is given that ∠ ECB = ∠ ECD.

AB is parallel to CD.

⇒ ∠ CEB = ∠ ECD (alternate angles)

So, ∠ CEB = ∠ ECB

BC = BE (sides opposite to equal angles are always equal)

And, we also know BC = AD (sides of parallelogram)

BE = AE (Given)

So, AD = AE (Using above equations)

Hence, AD = AE.

(ii)To prove:

∠ADE = ∠CDE

Proof:

∠ AED = ∠ ADE (angles opposite to equal sides are always equal)

AB is parallel to CD.

⇒ ∠ AED = ∠ EDC (alternate angles)

So, ∠ ADE = ∠ CDE

Hence, DE bisects ∠ ADC.

(iii)To prove:

∠ DEC = 90°

Proof:

AD is parallel to BC.

⇒ ∠D + ∠C = 180°

⇒ 2∠EDC + 2∠DCE = 180°

⇒ 2(∠EDC + ∠DCE) = 180°

⇒ ∠EDC + ∠DCE = $\dfrac{180°}{2}$

⇒ ∠EDC + ∠DCE = 90°

In triangle DEC, sum of all the angles is 180°

⇒ ∠EDC + ∠DCE + ∠DEC = 180°

⇒ 90° + ∠DEC = 180°

⇒ ∠DEC = 180° - 90°

⇒ ∠DEC = 90°

Hence, Angle DEC is a right angle.

In the diagram given below, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD. Show that:

(i) ∠PSB + ∠SPB = 90°

(ii) ∠PBS = 90°

(iii) ∠ABC = 90°

(iv) ∠ADC = 90°

(v) ∠A = 90°

(vi) ABCD is a rectangle

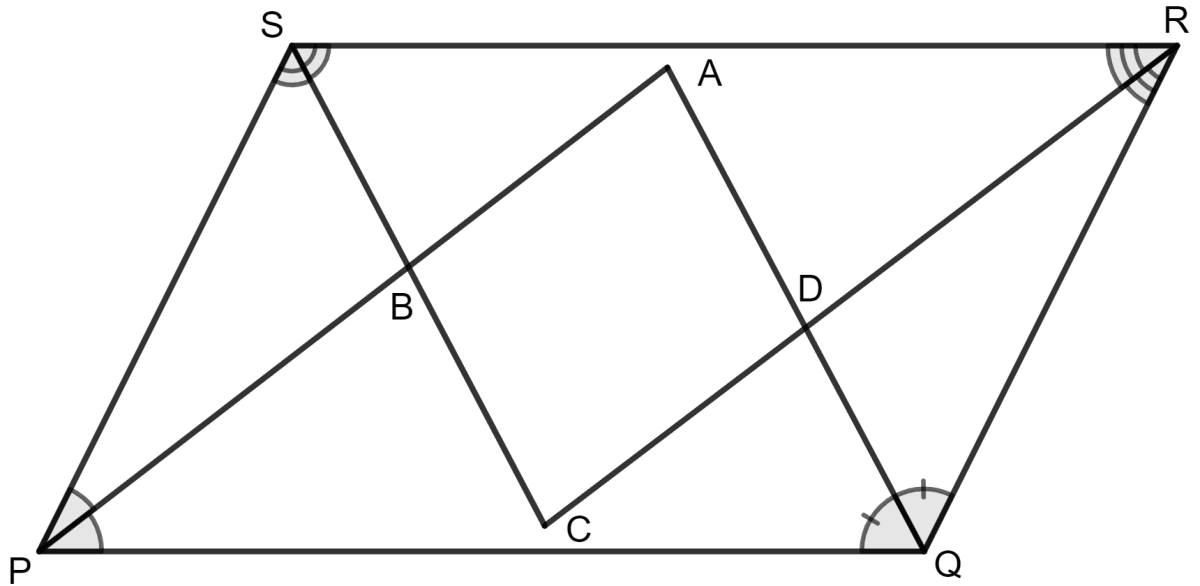
Answer

(i) Given:

PQRS is a parallelogram.

To prove:

∠PSB + ∠SPB = 90°

Proof:

It is given that AP and CS is an angle bisectors.

∠SPB = ∠BPQ and ∠PSB = ∠BSR

As PS is parallel to QR,

⇒ ∠SPQ + ∠PSR = 180°

⇒ $\dfrac{1}{2}$ (∠SPQ + ∠PSR) = $\dfrac{1}{2}$ 180°

⇒ $\dfrac{1}{2}$ ∠SPQ + $\dfrac{1}{2}$ ∠PSR = 90°

⇒ ∠SPB + ∠PSB= 90°

Hence, ∠PSB + ∠SPB = 90°.

(ii) To prove:

∠PBS = 90°

Proof:

In triangle PBS, the sum of all the angles is 180°.

⇒ ∠PSB + ∠SPB + ∠PBS = 180°

Using ∠PSB + ∠SPB = 90°, we get

⇒ 90° + ∠PBS = 180°

⇒ ∠PBS = 180° - 90°

⇒ ∠PBS = 90°

Hence, ∠PBS = 90°.

(iii)To prove:

∠ABC = 90°

Proof:

∠PBS = ∠ABC (vertically opposite angles)

∠PBS = 90°

So, ∠ABC = 90°

Hence, ∠ABC = 90°.

(iv) To prove:

∠ADC = 90°

Proof:

PQRS is a parallelogram.

As PS is parallel to QR,

⇒ ∠SRQ + ∠RQP = 180°

⇒ $\dfrac{1}{2}$ (∠SRQ + ∠RQP) = $\dfrac{1}{2}$ 180°

⇒ $\dfrac{1}{2}$ ∠SRQ + $\dfrac{1}{2}$ ∠RQP = 90°

⇒ ∠DRQ + ∠RQD = 90°

In triangle RDQ, the sum of all the angles is 180°.

⇒ ∠DRQ + ∠DQR + ∠QDR = 180°

Using ∠DRQ + ∠RQD = 90°, we get

⇒ 90° + ∠QDR = 180°

⇒ ∠QDR = 180° - 90°

⇒ ∠QDR = 90°

∠QDR = ∠ADC (vertically opposite angles)

So, ∠ADC = 90°

Hence, ∠ADC = 90°.

(v) To prove:

∠A = 90°

Proof:

In triangle APQ, the sum of all the angles is 180°.

⇒ ∠APQ + ∠AQP + ∠PAQ = 180°

⇒ (∠APQ + ∠AQP) + ∠PAQ = 180°

[∵ ∠ APQ = $\dfrac{1}{2}$ ∠ SPQ and ∠ AQP = $\dfrac{1}{2}$ ∠ RQP ]

As we know opposite side of parallelogram are equal.

So, ∠ RQP = ∠ PSR

Therefore, ∠ AQP = $\dfrac{1}{2}$ ∠ PSR

⇒ $\dfrac{1}{2}$ (∠SPQ + ∠PSR) + ∠PAQ = 180°

⇒ 90° + ∠PAQ = 180°

⇒ ∠PAQ = 180° - 90°

⇒ ∠PAQ = 90°

Hence, ∠A = 90°.

(vi) To prove:

ABCD is a rectangle.

Proof:

∠A = ∠B = ∠D = 90°

Sum of each angle of quadrilateral is 360°.

⇒ ∠A + ∠B + ∠C + ∠D = 360°

⇒ 90° + 90° + ∠C + 90° = 360°

⇒ 270° + ∠C = 360°

⇒ ∠C = 360° - 270°

⇒ ∠C = 90°

Each angle of the quadrilateral is 90°.

Hence, ABCD is a rectangle.

In a parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:

(i) AX = YC.

(ii) AX is parallel to YC

(iii) AXCY is a parallelogram.

Answer

(i) Given:

ABCD is a parallelogram.

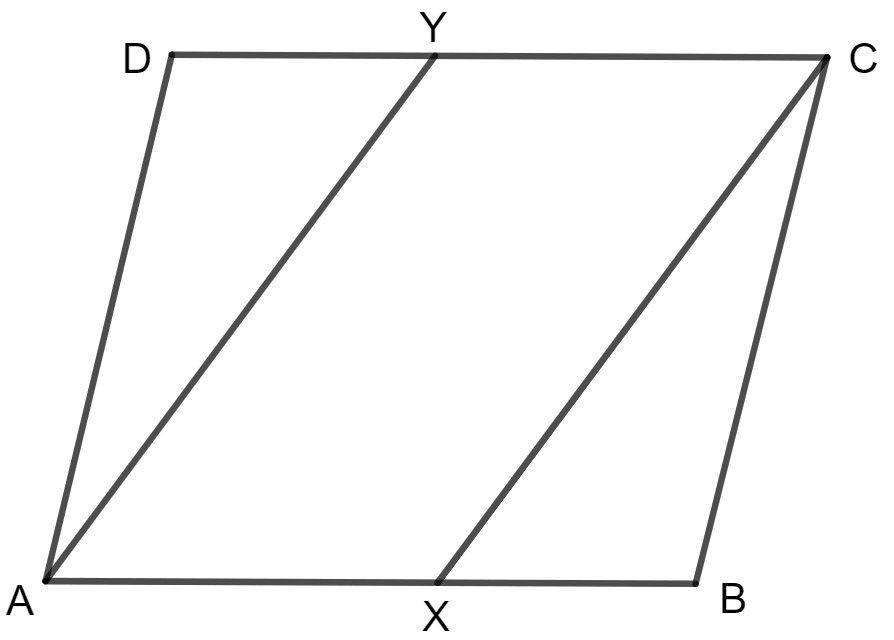
To prove:

AX = YC.

Proof:

We know that, opposite sides of parallelogram are equal.

AB = CD

⇒ $\dfrac{1}{2}$ AB = $\dfrac{1}{2}$ CD

⇒ AX = CY (As, X and Y are mid - points of AB and CD respectively)

Hence, AX = YC.

(ii) To prove:

AX is parallel to YC.

Proof:

Opposite sides of parallelogram are equal.

AB is parallel to DC.

⇒ AX is parallel to YC.

Hence, AX is parallel to YC.

(iii) To prove:

AXCY is a parallelogram.

Proof:

AX = YC

And, AX is parallel to YC.

Since, one pair of opposite sides of quadrilateral AXCY are equal and parallel.

Hence, AXCY is a parallelogram.

The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN. Prove that:

(i) △DMC ≅ △BNA and so CM = AN.

(ii) △AMD ≅ △CNB and so AM = CN.

(iii) ANCM is a parallelogram.

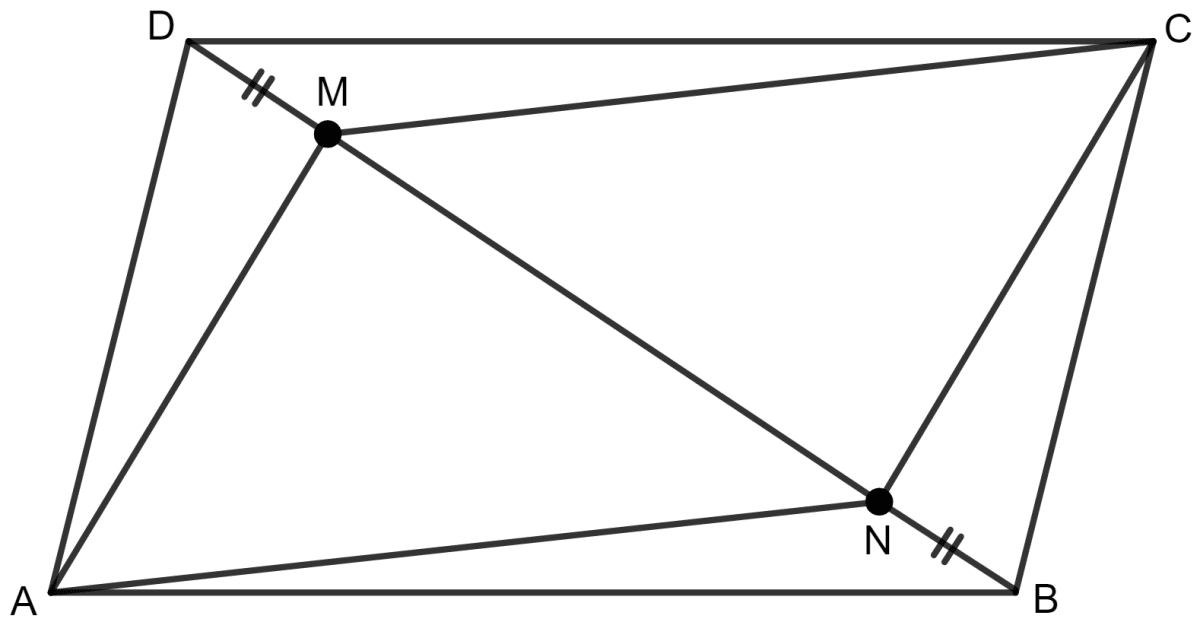
Answer

(i) Given:

ABCD is a parallelogram.

To prove:

△DMC ≅ △BNA and so CM = AN

Proof:

In triangle DMC and BNA,

CD = AB (opposite sides of parallelogram)

DM = BN (Given)

∠ CDM = ∠ ABN (alternate angles)

So, by Side Angle Side congruency,

△DMC ≅ △BNA

By using Corresponding Parts of Congruent Triangles,

CM = AN

Hence, △DMC ≅ △BNA and CM = AN.

(ii)To prove:

△AMD ≅ △CNB and so AM = CN.

Proof:

In triangle AMD and CNB,

AD = BC (opposite sides of parallelogram)

DM = BN (Given)

∠ ADM = ∠ CBN (alternate angles)

So, by Side Angle Side congruency,

△AMD ≅ △CNB

By using Corresponding Parts of Congruent Triangles,

AM = CN

Hence, △AMD ≅ △CNB and so AM = CN.

(iii)To prove:

ANCM is a parallelogram.

Proof:

CM = AN (proved)

AM = CN (proved)

Hence, ANCM is a parallelogram.

The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

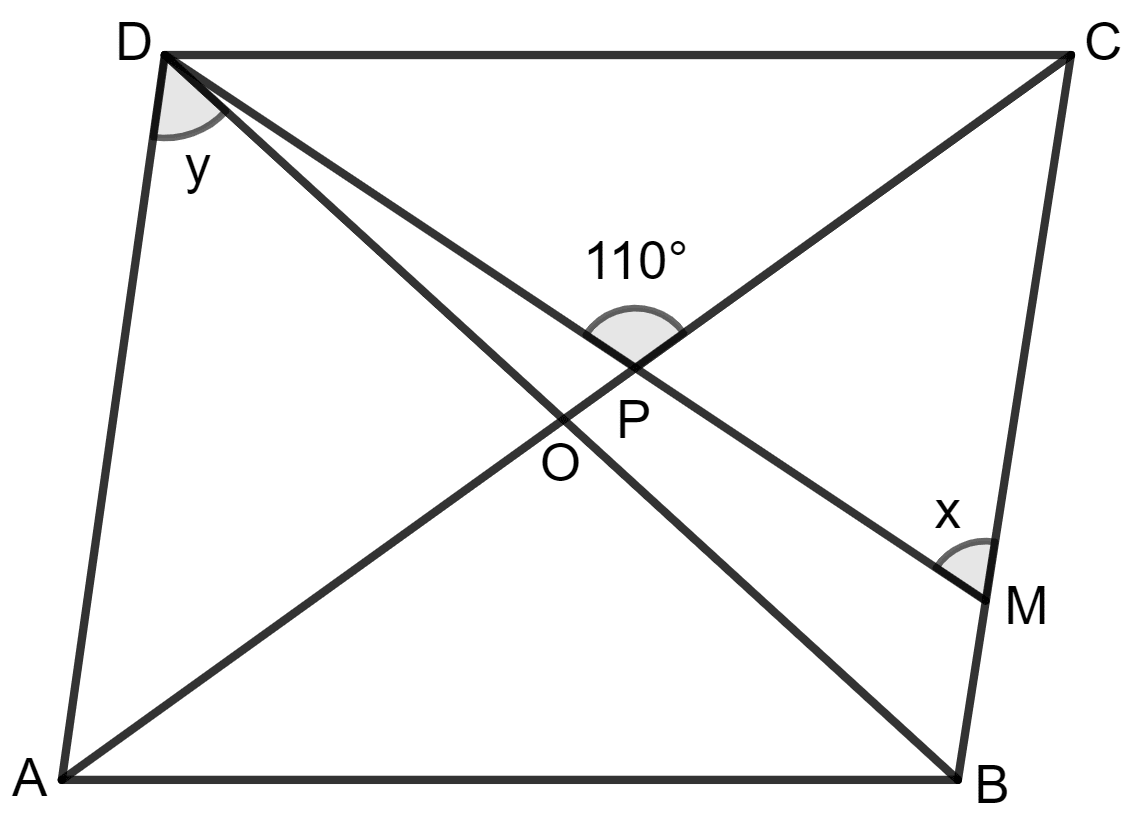
Answer

It is given that in rhombus ABCD, diagonal AC and BD bisect each other at 90° and ∠ BCD = 80°.

Also, ∠BCD = ∠ BAD (opposite angles of rhombus)

⇒ ∠ BAD = 80°

Adjacent angles of a quadrilateral are supplementary.

So, ∠BCD + ∠CDA = 180°

⇒ 80° + ∠CDA = 180°

⇒ ∠CDA = 180° - 80°

⇒ ∠CDA = 100°

And, ∠ ADB = $\dfrac{1}{2}$ ∠ ADC

⇒ y = $\dfrac{1}{2}$ 100°

⇒ y = 50°

Also, ∠CDA = ∠ ABC (opposite angles of rhombus)

⇒ ∠ ABC = 100°

Diagonals bisect opposite angles.

∠ OCB or ∠ PCB = $\dfrac{1}{2}$ ∠ BCD

= $\dfrac{1}{2}\times$ 80°

= 40°

Consider triangle PCM,

Exterior angle = sum of opposite interior angles.

∠ CPD = ∠ PCM + ∠ PMC

⇒ 110° = 40° + x

⇒ x = 110° - 40°

⇒ x = 70°

Hence, the value of x = 70° and y = 50°.

Use the information given in the following diagram to find the values of x, y and z.

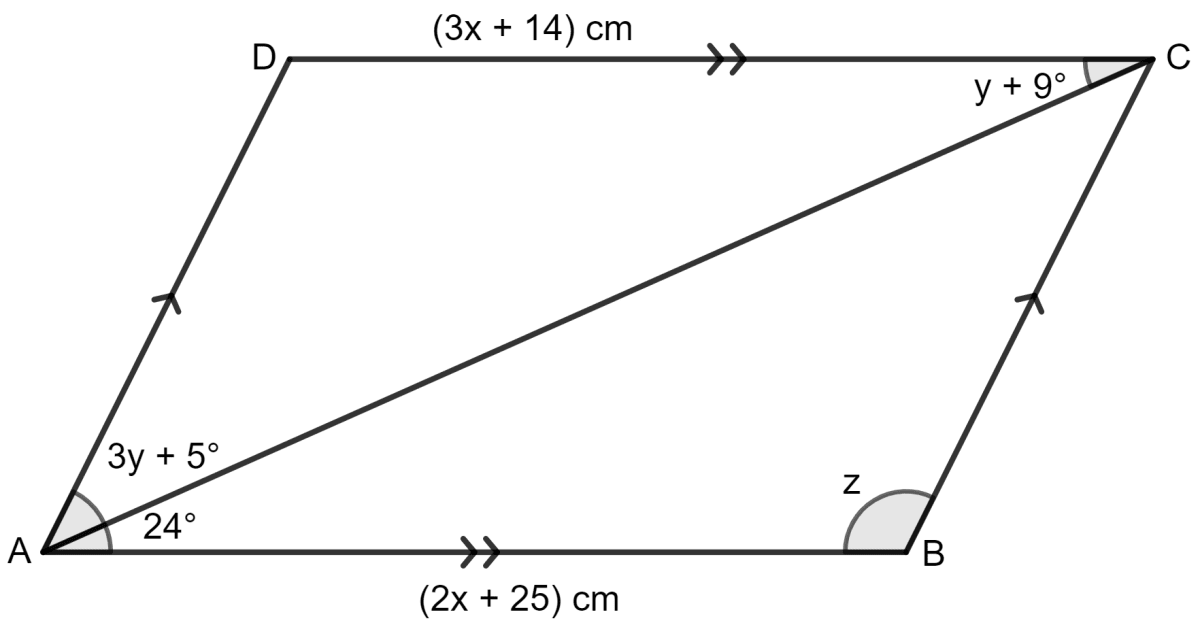
Answer

ABCD is a parallelogram and AC is its diagonal which bisects the opposite angle.

Opposite sides of a parallelogram are equal.

⇒ 3x + 14 = 2x + 25

⇒ 3x - 2x = 25 - 14

⇒ x = 11

In the parallelogram,

∠ DCA = ∠ CAB (alternate angles)

⇒ y + 9° = 24°

⇒ y = 24° - 9°

⇒ y = 15°

∠ DAB = (3y + 5 + 24)°

= (3 $\times$ 15 + 5 + 24)°

= (45 + 29)°

= 74°

∠ ABC = z = 180° - ∠ DAB

⇒ z = 180° - 74°

⇒ z = 106°

Hence, the value of x = 11 cm, y = 15° and z = 106°.

The following figure is a rectangle in which x : y = 3 : 7; find the values of x and y.

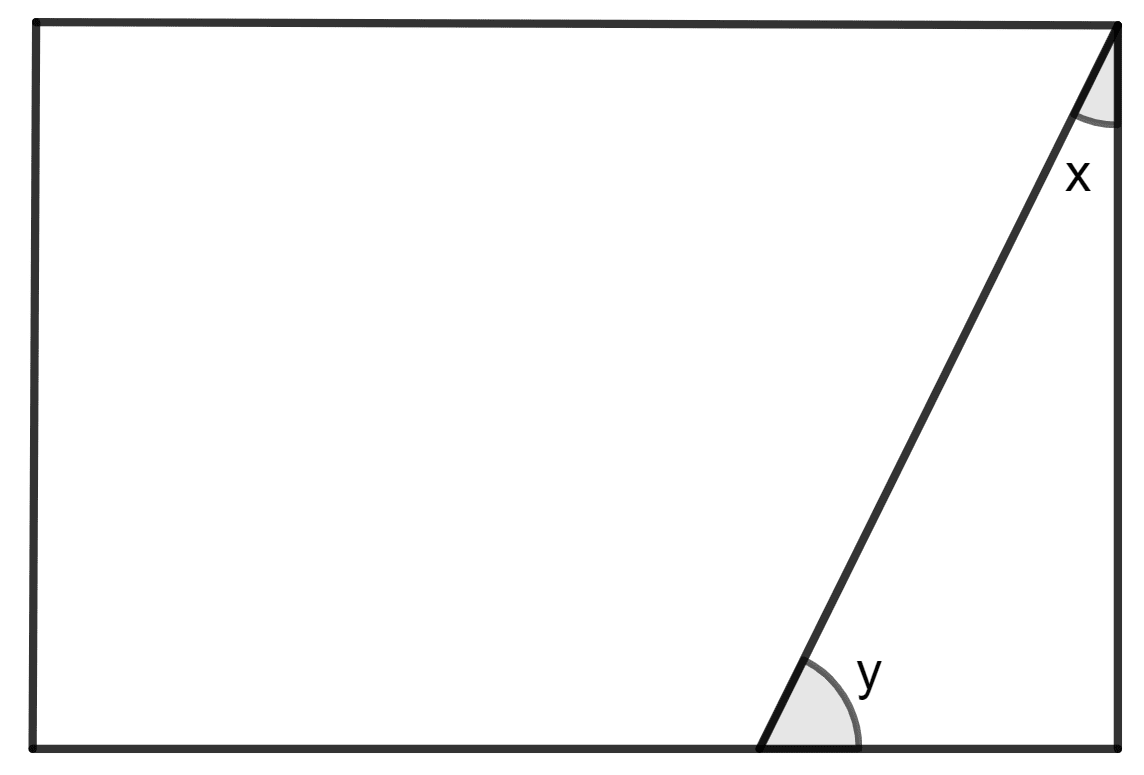
Answer

It is given that ABCD is a rectangle in which x : y = 3 : 7.

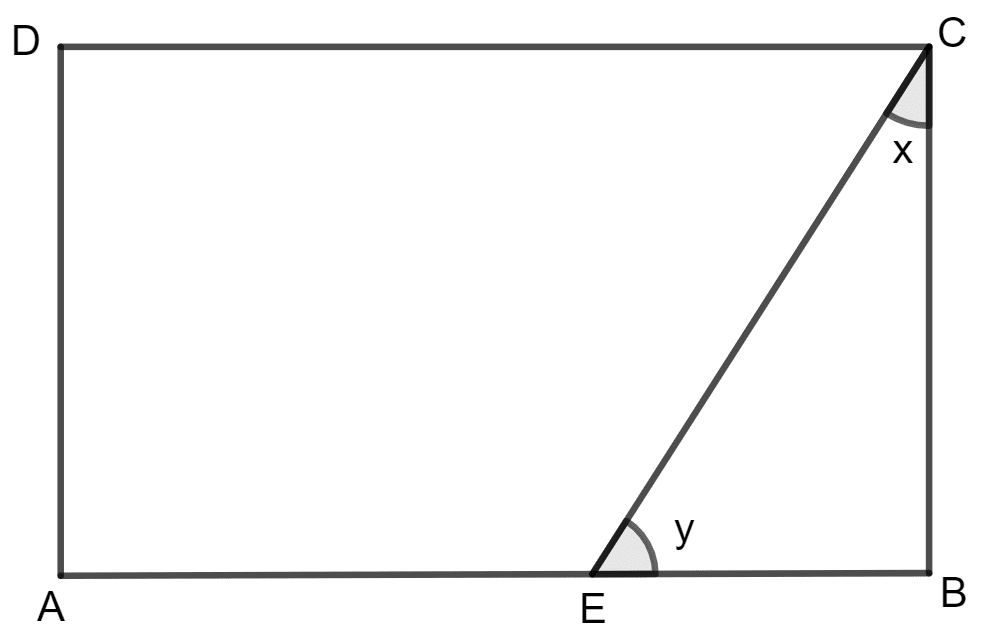
Let ∠ BEC be 3a and ∠ BCE = 7a

In triangle BEC, sum of all the angles is 180°.

⇒ ∠ BEC + ∠ BCE + ∠ CBE = 180°

⇒ 3a + 7a + 90° = 180° (each angle of rectangle is 90°)

⇒ 10a + 90° = 180°

⇒ 10a = 180° - 90°

⇒ 10a = 90°

⇒ a = $\dfrac{90°}{10}$

⇒ a = 9°

So, ∠ BEC = x = 3 $\times$ 9° and ∠ BCE = y = 7 $\times$ 9°

⇒ x = 27° and y = 63°

Hence, the value of x = 27° and y = 63°.

In the given figure, AB // EC, AB = AC and AE bisects ∠DAC. Prove that:

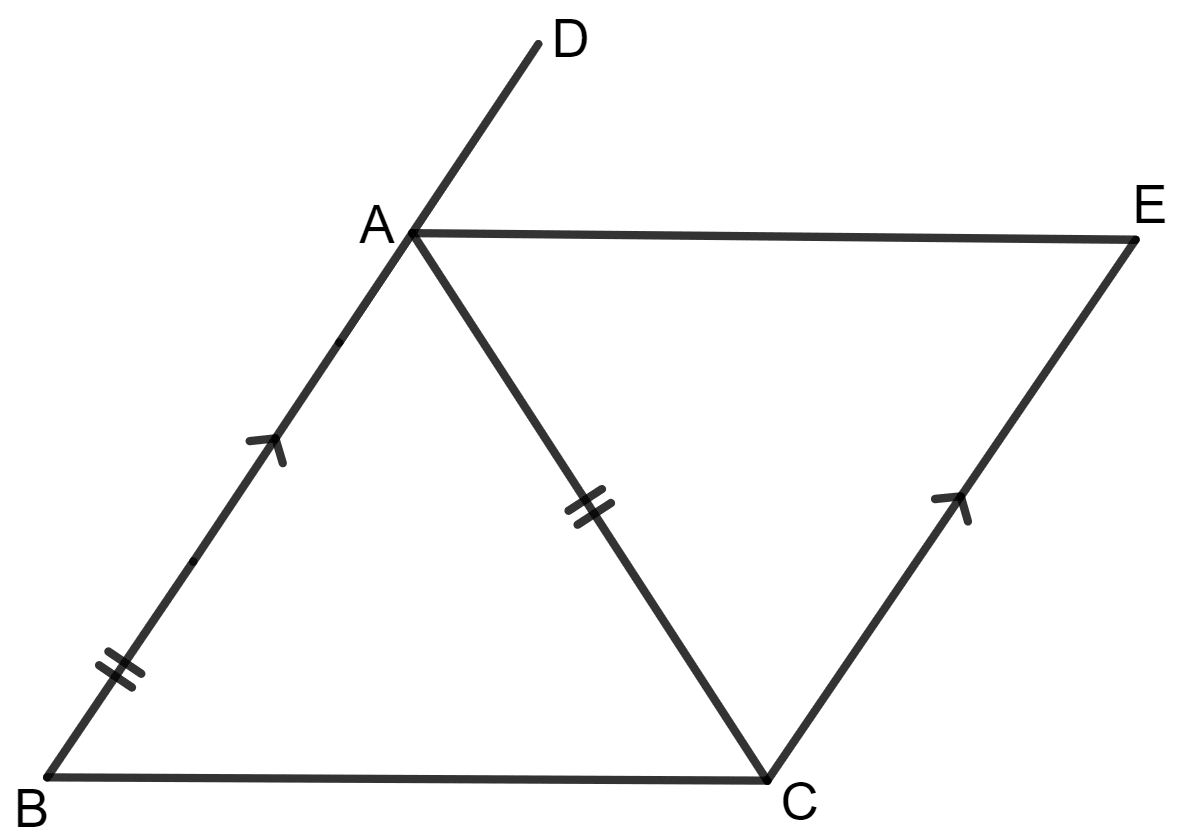
(i) ∠EAC = ∠ACB

(ii) ABCE is a parallelogram.

Answer

(i) Given :

AB // EC, AB = AC and AE bisects ∠DAC.

To prove :

∠EAC = ∠ACB

Proof :

In triangle ABC and AEC,

AC = AC (Common)

AB = AC (Given)

∠ BAC = ∠ AEC

By Side Angle Side congruency,

Δ ABC ≅ Δ AEC

By using Corresponding Parts of Congruent Triangles,

∠EAC = ∠ACB

(ii) To prove :

ABCE is a parallelogram.

Proof :

∠EAC = ∠ACB (Proved)

Hence, AE // BC

AB // EC (Given)

Hence, ABCE is a parallelogram.