Mathematics
A bag contains white, black and red balls only. A ball is drawn at random from the bag. If the probability of getting a white ball is and that of a black ball is , then find the probability of getting a red ball. If the bag contains 20 black balls, then find the number of balls in the bag.
Probability
16 Likes
Answer
Let probability of getting red ball be x.
We know that,
Probability of getting white, red and black balls are complementary events.
∴ Probability of getting white ball + Probability of getting red ball + Probability of getting black ball = 1
Given,
Probability of getting black ball =
Hence, probability of drawing red ball = and total balls = 50.
Answered By
11 Likes
Related Questions
Prove that :
sin A(1 + tan A) + cos A(1 + cot A) = sec A + cosec A
If the ninth term of an A.P. is zero. Show that its 29th term is twice the 19th term.
A solid, in the form of a right circular cone, is mounted on a hemisphere of the same radius. The radius of the hemisphere is 2.1 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical tub full of water in such a way that the whole solid is submerged in water. If the radius of the tub is 5 cm and its height is 9.8 cm, find the volume of water left in the tub.
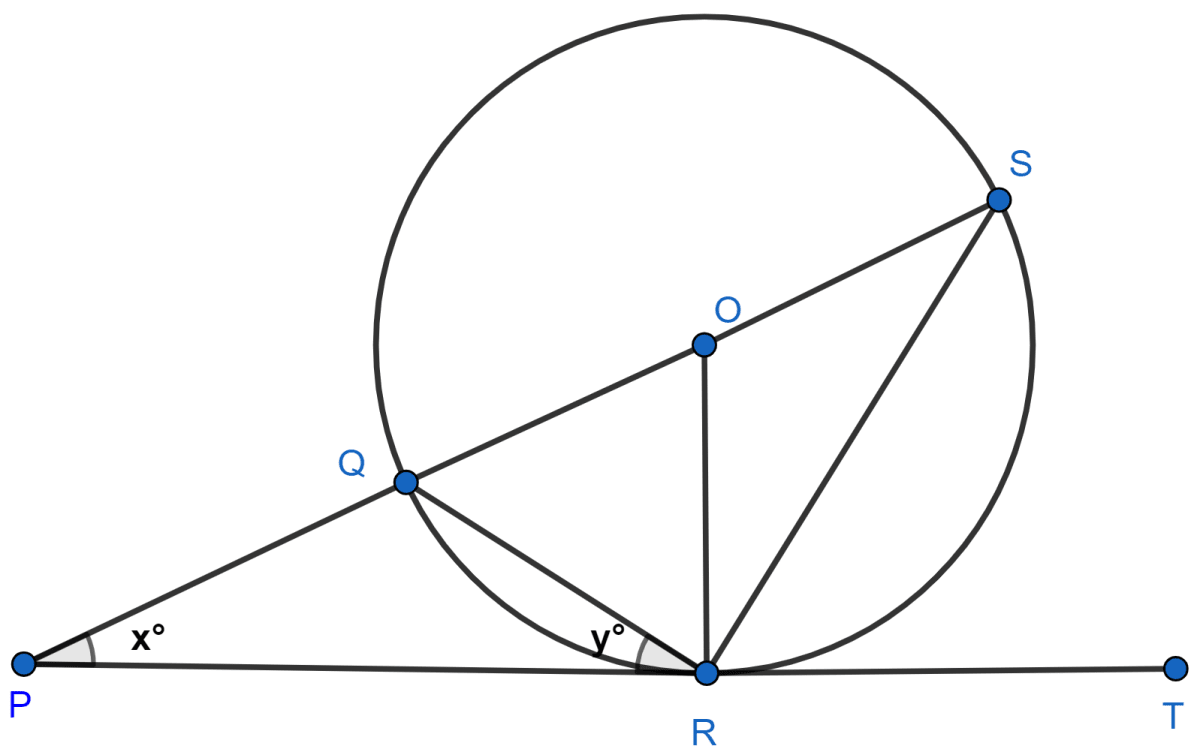
In the given figure, PT touches the circle, whose center is at point O, at point R. Diameter SQ produced meets tangent PT at point P. If angle SPR = x° and angle QRP = y°; find :
(i) angle ORQ in terms of y°.
(ii) a relation between x and y.