Mathematics
A chord of length 8 cm is drawn at a distance of 3 cm from the center of a circle. Calculate the radius of the circle.
Circles
49 Likes
Answer
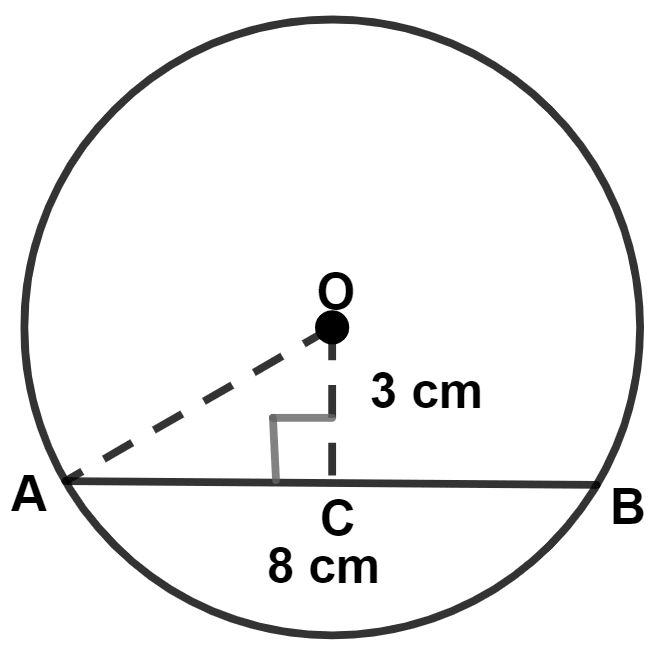
Let AB = 8 cm be the chord of the circle with center O.
We know that,
Perpendicular from center to chord, bisects the chord.
∴ AC = = 4 cm.
In right angled triangle OAC,
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ OA2 = OC2 + AC2
⇒ OA2 = 32 + 42
⇒ OA2 = 9 + 16
⇒ OA2 = 25
⇒ OA = = 5 cm.
Hence, radius of circle = 5 cm.
Answered By
29 Likes
Related Questions
The line joining the mid-points of two chords of a circle passes through its center, then the chords are :
not parallel to each other
equal to each other
parallel to each other
not equal to each other
In the given figure, O and O' are centers of two circles, AB // CD // OO', then which of the following is not true :
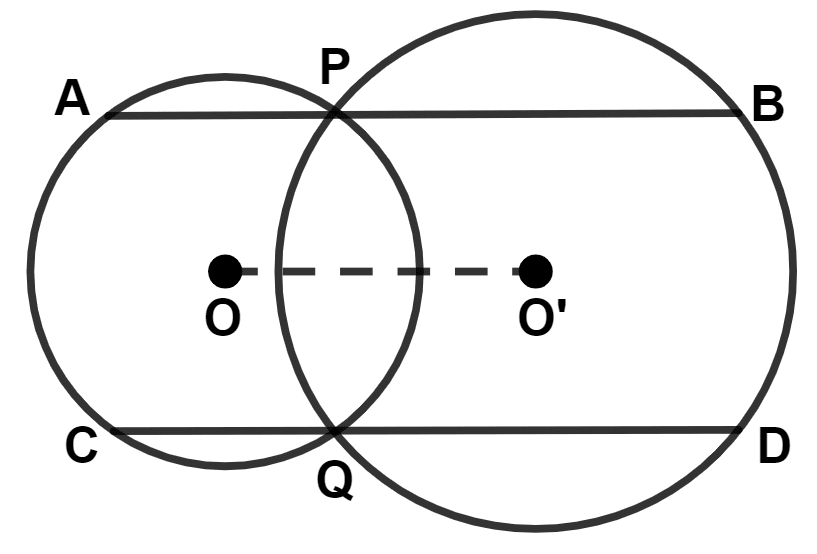
AB = 2 × OO'
CD = 2 × OO'
AB = CD
AB ≠ CD
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its center to a chord is 8.0 cm. Calculate the length of the chord.
A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.