Mathematics
A point P is at a distance 13 cm from the centre C of a circle, and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Circles
27 Likes
Answer
The below diagram shows the circle and the tangent:
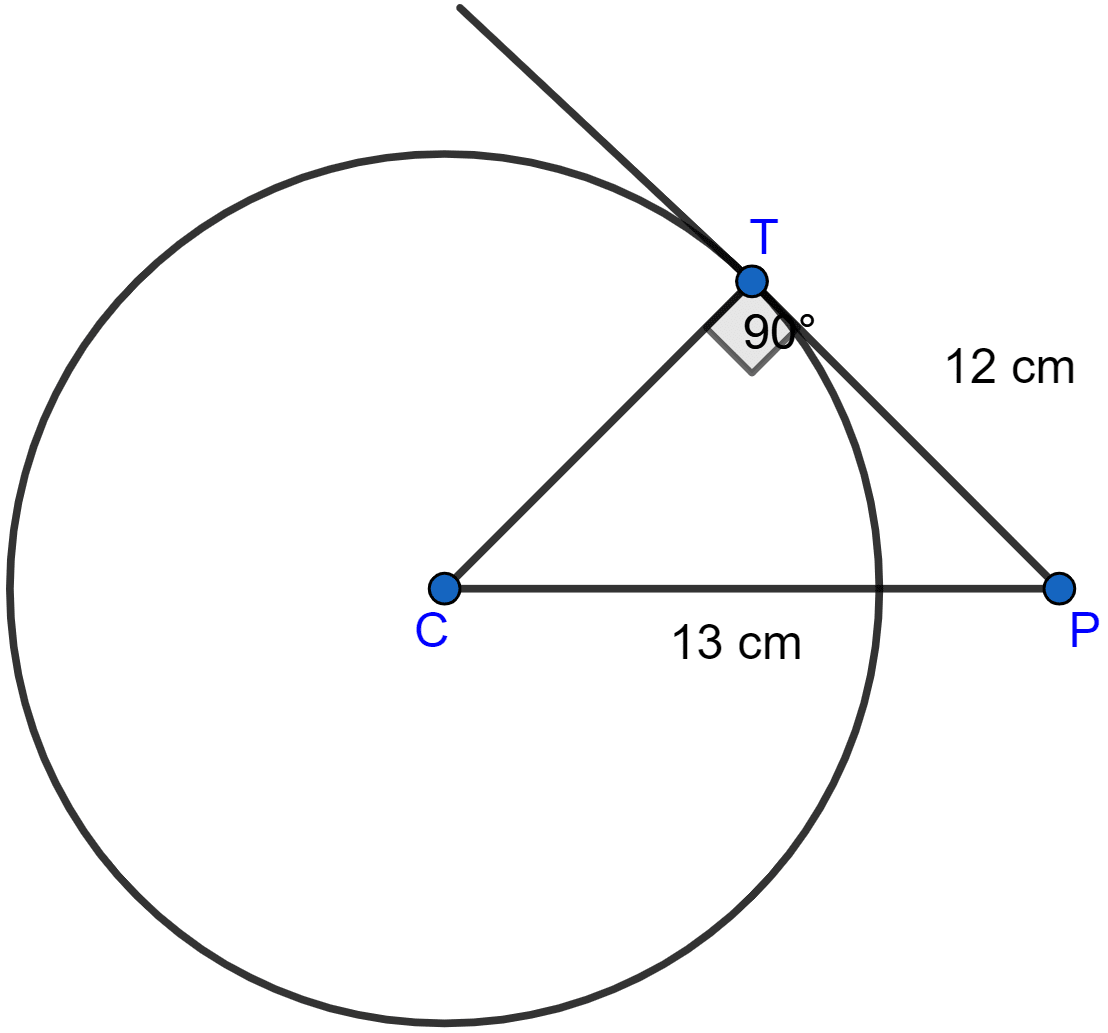
Given point P is 13 cm away from centre C, so CP = 13 cm.
PT = 12 cm
CT = radius of the circle.
Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.
So, CT ⊥ PT
So, in right angled △CPT by pythagoras theorem,
Hence, radius of circle = 5 cm.
Answered By
13 Likes
Related Questions
In the adjoining figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, calculate AB. Also find

Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
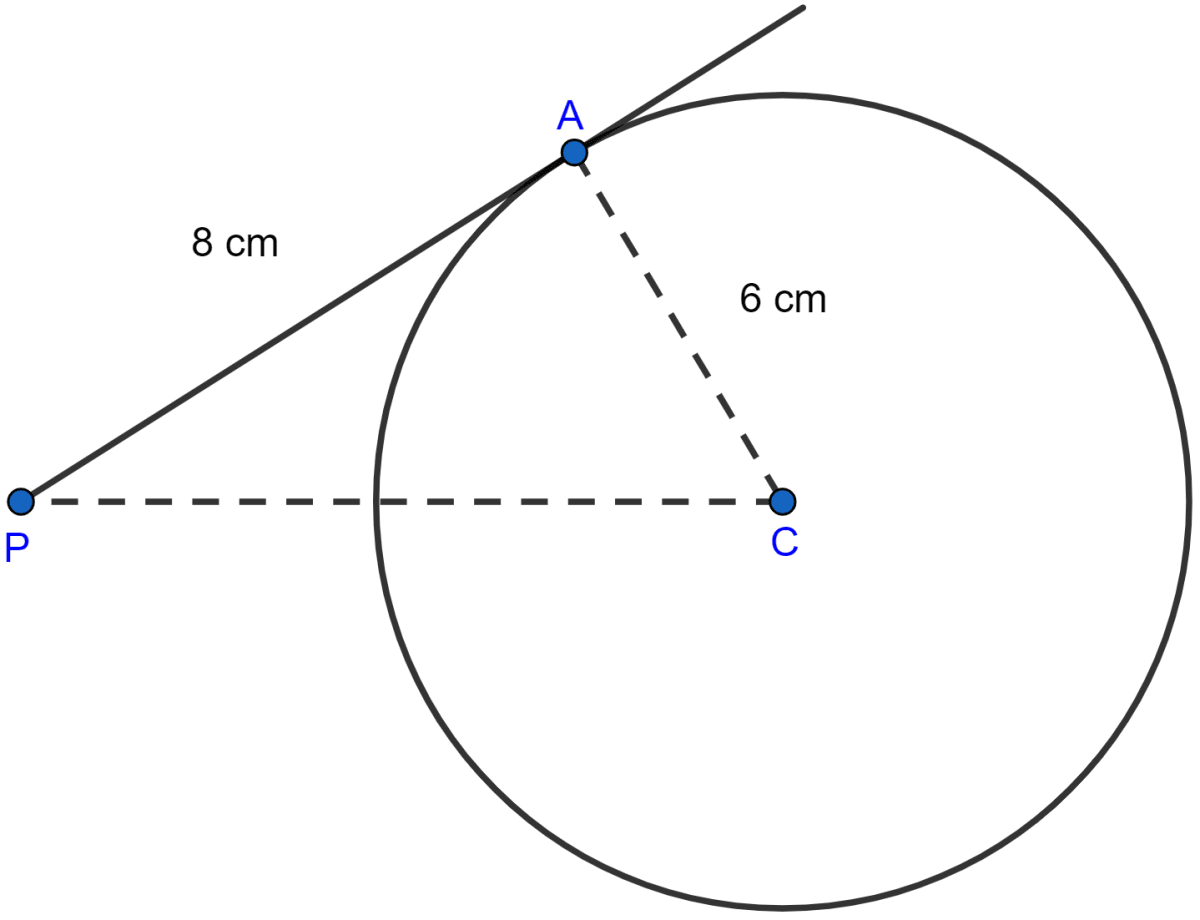
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
The figure shows a circle of radius 9 cm with O as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ.
