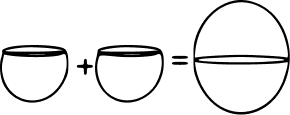Mathematics
A right circular cone has the radius of the base equal to the height of the cone. If the volume of the cone is 9702 cu. cm, then the diameter of the base of the cone is :
21 cm
42 cm
cm
cm
Mensuration
20 Likes
Answer
Given,
Height of cone (h) = Radius of cone (r) = a cm (let)
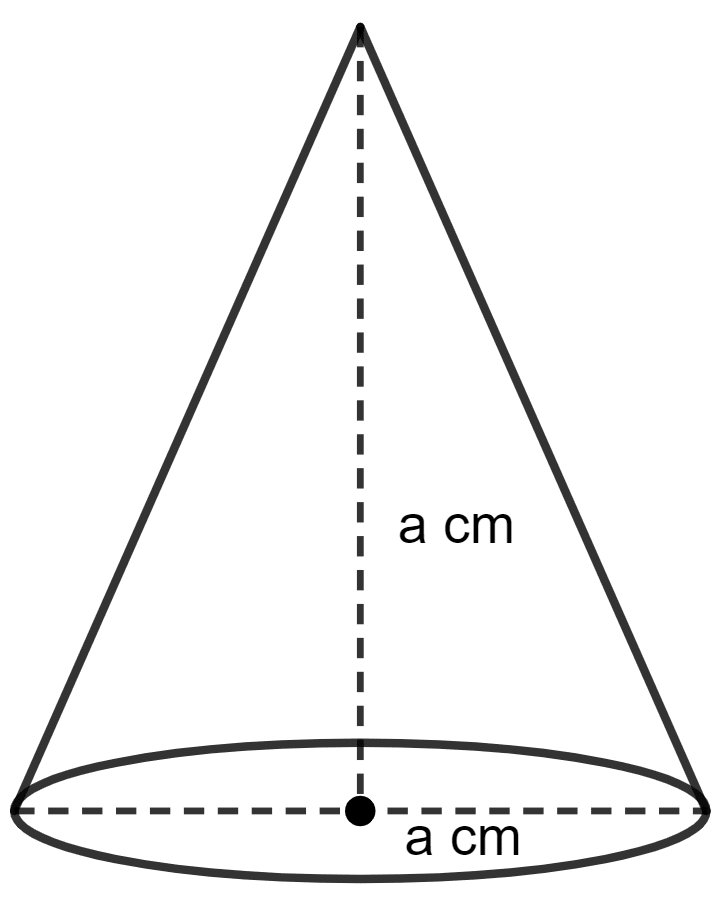
Given,
Volume = 9702 cm3
Diameter = 2 × radius = 2 × 21 = 42 cm.
Hence, Option 2 is the correct option.
Answered By
12 Likes
Related Questions
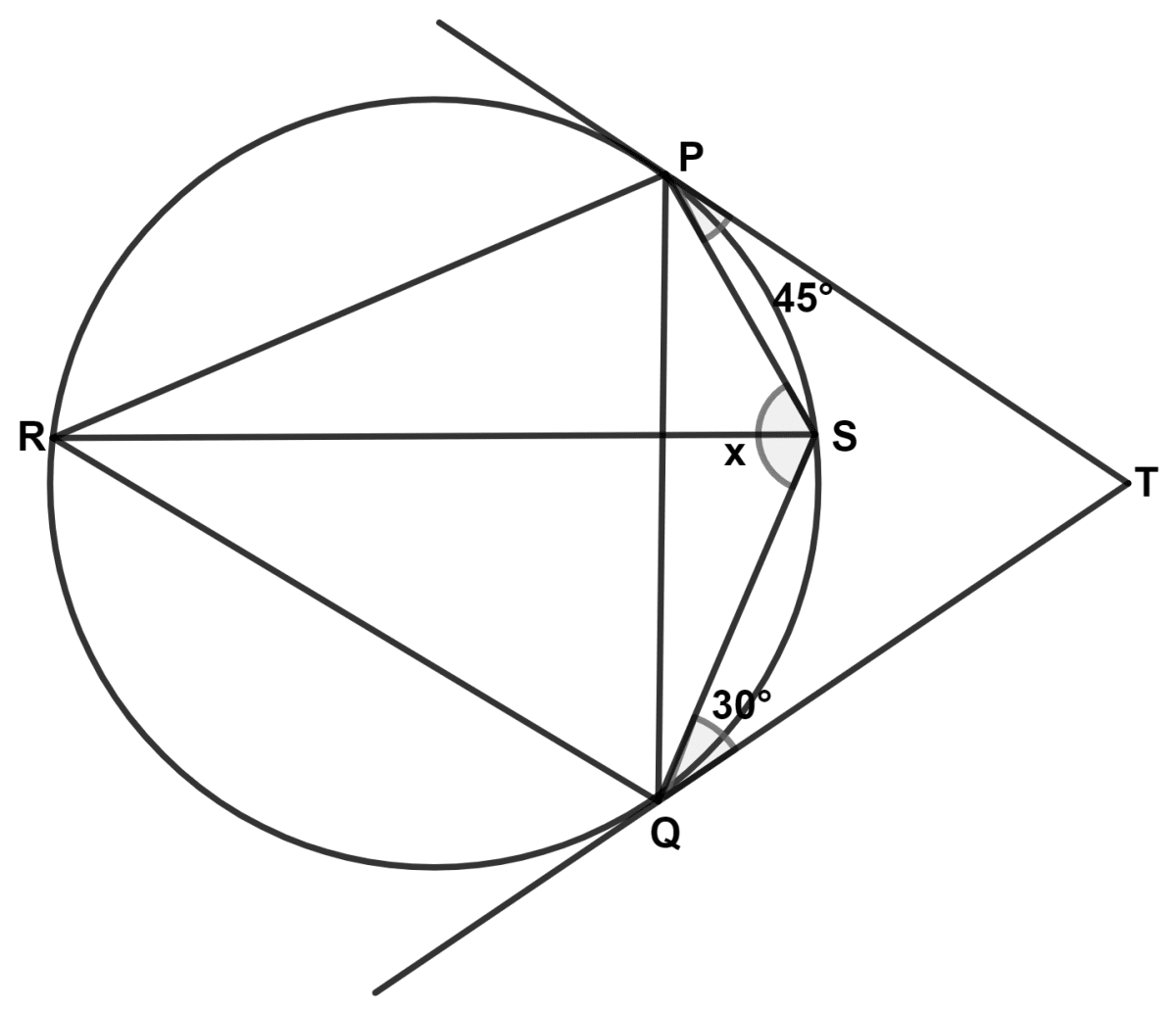
In the given figure, PT and QT are tangents to a circle such that ∠TPS = 45° and ∠TQS = 30°. Then, the value of x is :
30°
45°
75°
105°
A cylindrical metallic wire is stretched to double its length. Which of the following will NOT change for the wire after stretching?
Its curved surface area
Its total surface area
Its volume
Its radius
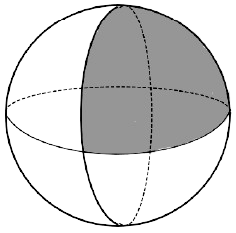
A solid sphere with a radius of 4 cm is cut into 4 identical pieces by two mutually perpendicular planes passing through its center. Find the total surface area of one-quarter piece.
24π
32π
48π
64π
Two identical solid hemispheres are kept in contact to form a sphere. The ratio of the total surface areas of two hemispheres to the surface area of the sphere formed is :
1 : 1
3 : 2
2 : 3
2 : 1