Mathematics
A triangle ABC has ∠B = ∠C. Prove that :
(i) the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) the perpendicular from B and C to the opposite sides are equal.
Answer
△ ABC is shown in the figure below:
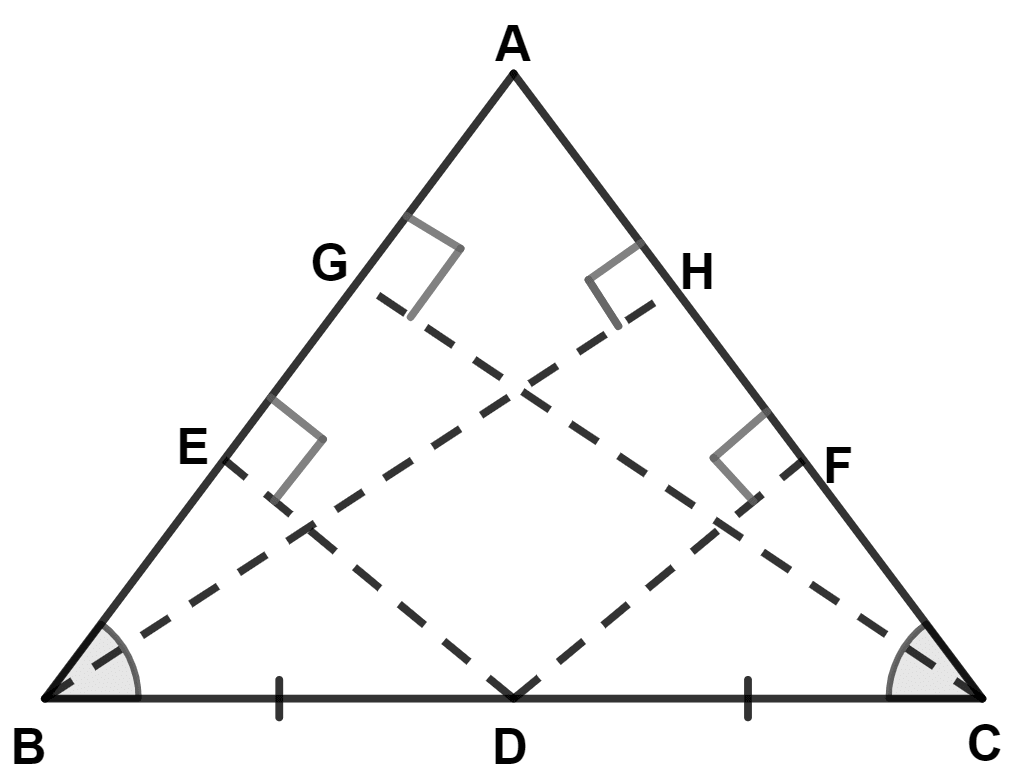
(i) From figure,
In △ BDE and △ CDF,
⇒ BD = CD (As D is the mid-point of BC)
⇒ ∠B = ∠C (Given)
⇒ ∠DEB = ∠CFD (Both equal to 90°)
∴ △ BDE ≅ △ CDF (By A.A.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ DE = DF.
Hence, proved that the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) Let perpendiculars from B and C touch sides AC and AB at point H and G.
From figure,
In △ ABH and △ ACG,
⇒ ∠AHB = ∠AGC (Both equal to 90°)
⇒ ∠BAH = ∠CAG (Common angle)
⇒ ∠HBA = ∠GCA (Since, two angles of a triangle are equal so third angle is also equal)
∴ △ ABH ≅ △ ACG (By A.A.A. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ BH = GC.
Hence, proved that the perpendicular from B and C to the opposite sides are equal.
Related Questions
In quadrilateral ABCD, AB = AC and BD = CD, then AD bisects :
angle ADC
angle BAD
angle BAC
angle ABC
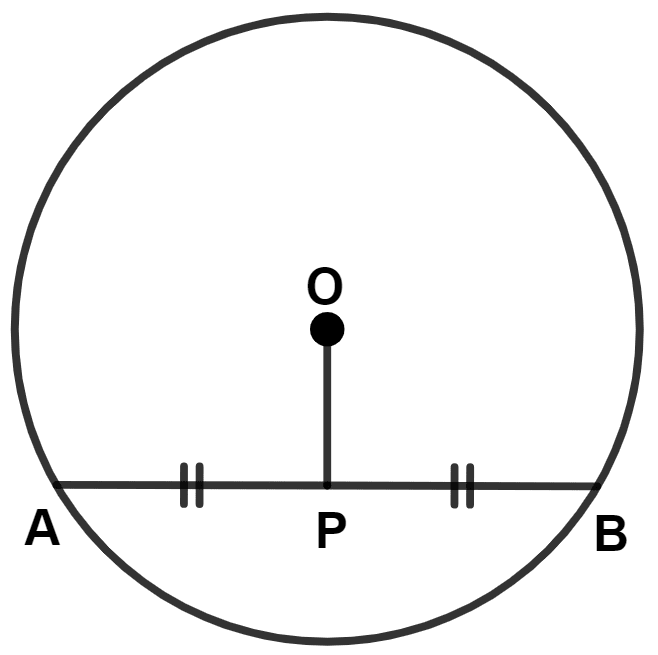
The given figure shows a circle with center O. P is mid-point of chord AB. Show that OP is perpendicular to AB.
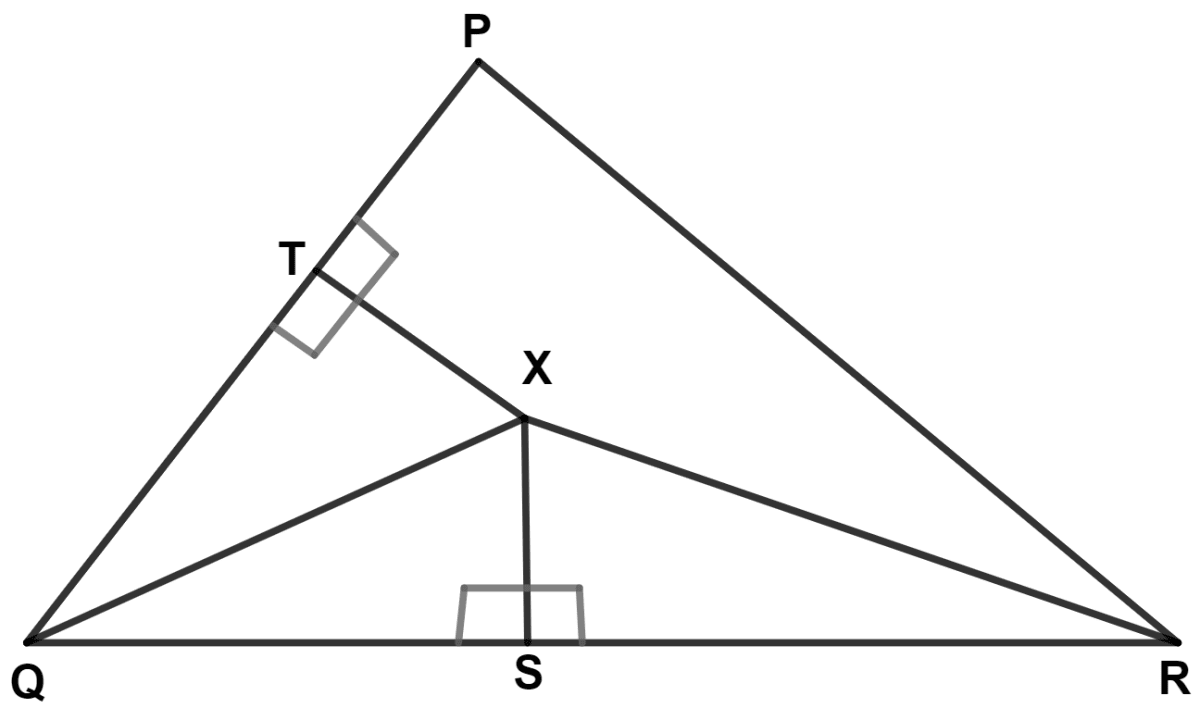
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR. If XS ⊥ QR and XT ⊥ PQ; prove that :
(i) △ XTQ ≅ △ XSQ
(ii) PX bisects angle P.
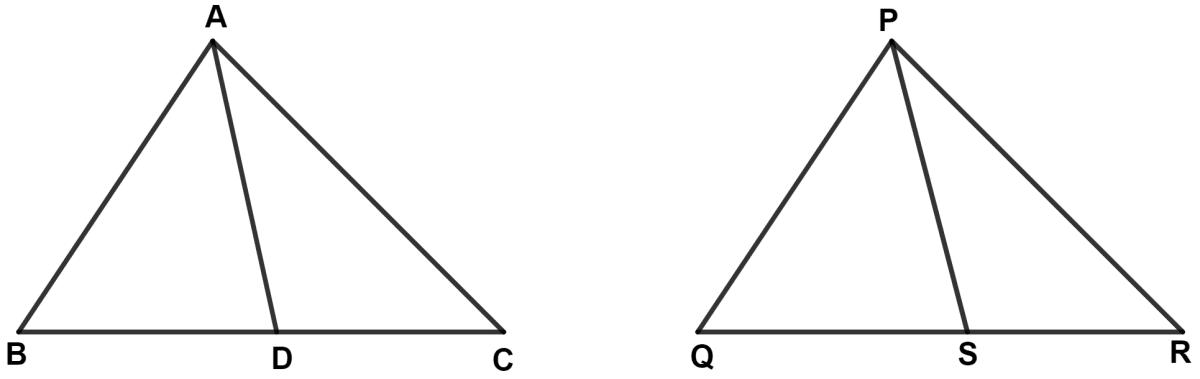
In the following figures, the sides AB and BC and the median AD of the triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that △ ABC and △ PQR are congruent.