Mathematics
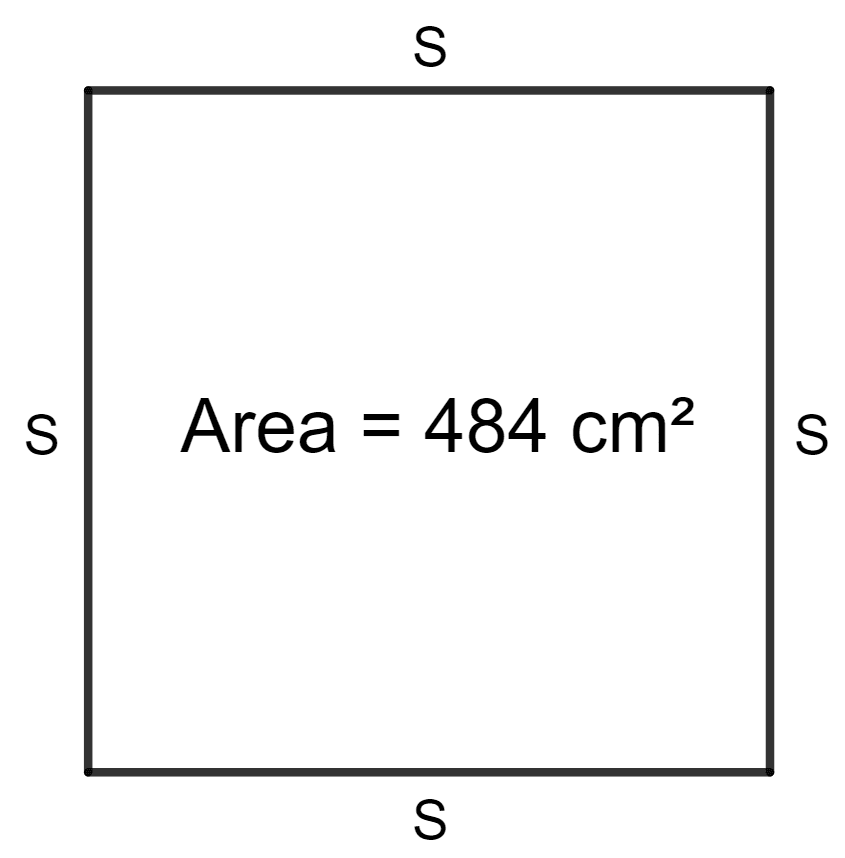
A wire, when bent in the form of a square, encloses an area of 484 cm2. Find :
(i) one side of the square
(ii) length of the wire
(iii) the largest area enclosed, if the same wire is bent to form a circle.
Area Trapezium Polygon
6 Likes
Answer
Given:
Area of the square = 484 cm2
Let s be the side of the square.
As we know, the area of the square = side2
⇒ s2 = 484
⇒ s =
⇒ s = 22
Hence, one side of square is 22 cm.
(ii) Total length of the wire = perimeter of the square
As we know, the perimeter of the square = 4 x side
= 4 x 22
= 88 cm
Hence, the length of the wire is 88 cm.
(iii) Perimeter of the square = circumference of the circle
Let r be the radius of the circle.
⇒ 2πr = 88 cm
Area of the circle = πr2
Hence, the largest area that can be enclosed when the same wire is bent to form a circle is 616 cm2.
Answered By
2 Likes
Related Questions
The radii of the inner and outer circumferences of a circular-running-track are 63 m and 70 m respectively. Find :
(i) the area of the track
(ii) the difference between the lengths of the two circumferences of the track
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
A wire, when bent in the form of a square, encloses an area of 196 cm2. If the same wire is bent to form a circle, find the area of the circle.
The radius of a circular wheel is 42 cm. Find the distance traveled by it in :
(i) 1 revolution
(ii) 50 revolutions
(iii) 200 revolutions