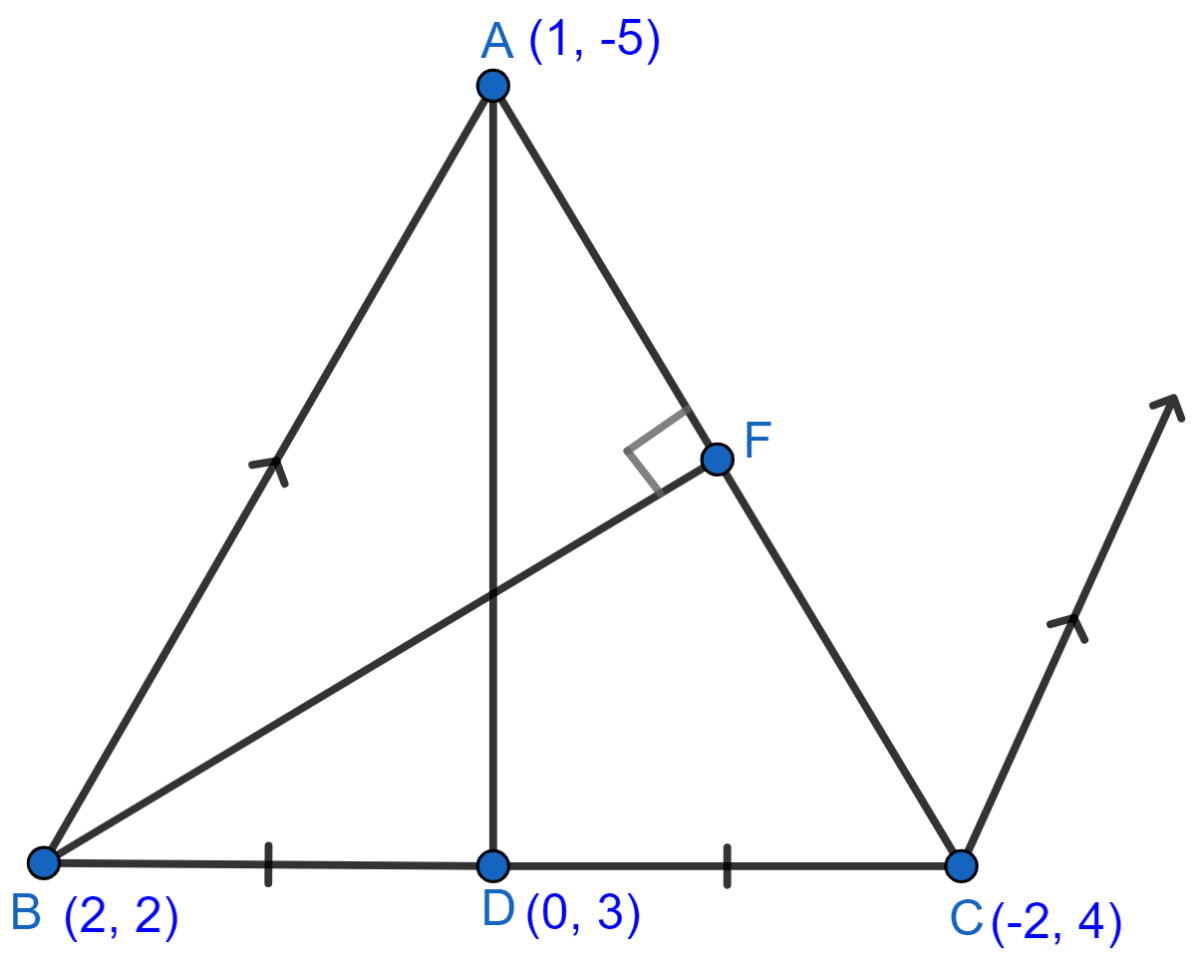
A(1, -5), B(2, 2) and C(-2, 4) are the vertices of triangle ABC. Find the equation of :

(i) the median of the triangle through A.

(ii) the altitude of the triangle through B.

(iii) the line through C and parallel to AB.

(i) Let AD be the median through A.

So, D will be the mid-point of BC.

Co-ordinates of D = $\Big(\dfrac{x$1 + x2}{2}, \dfrac{y1 + y2}{2}\Big) = \Big(\dfrac{2 + (-2)}{2}, \dfrac{2 + 4}{2}\Big) = \Big(\dfrac{0}{2}, \dfrac{6}{2}\Big) = (0, 3).

$\text{Slope of AD } = \dfrac{y$2 - y1}{x2 - x1} \\[1em] = \dfrac{3 - (-5)}{0 - 1} \\[1em] = -\dfrac{8}{1} \\[1em] = -8.

⇒ y - y₁ = m(x - x₁)

⇒ y - (-5) = -8(x - 1)

⇒ y + 5 = -8x + 8

⇒ 8x + y = 3.

Hence, equation of median through A is 8x + y = 3.

(ii) Let BF be the altitude.

$\text{Slope of AC } = \dfrac{y$2 - y1}{x2 - x1} \\[1em] = \dfrac{4 - (-5)}{-2 - 1} \\[1em] = \dfrac{9}{-3} \\[1em] = -3.

Since, altitude is at 90°.

So, altitude through B (i.e. BF) will be perpendicular to AC.

Let slope of altitude through B be m.

∴ m × -3 = -1

⇒ m = $\dfrac{1}{3}$.

Equation of altitude through B by point-slope form,

⇒ y - y₁ = m(x - x₁)

⇒ y - 2 = $\dfrac{1}{3}$(x - 2)

⇒ 3(y - 2) = x - 2

⇒ 3y - 6 = x - 2

⇒ x - 3y - 2 + 6 = 0

⇒ x - 3y + 4 = 0.

Hence, equation of altitude through B is x - 3y + 4 = 0.

(iii) $\text{Slope of AB } = \dfrac{y$2 - y1}{x2 - x1} \\[1em] = \dfrac{2 - (-5)}{2 - 1} \\[1em] = \dfrac{7}{1} \\[1em] = 7.

Since, parallel lines have equal slopes.

So slope of line through C and parallel to AB = 7.

Equation of line through C by point-slope form,

⇒ y - y₁ = m(x - x₁)

⇒ y - 4 = 7[x - (-2)]

⇒ y - 4 = 7(x + 2)

⇒ y - 4 = 7x + 14

⇒ 7x - y + 14 + 4 = 0

⇒ 7x - y + 18 = 0.

Hence, equation of line through C and parallel to AB is 7x - y + 18 = 0.