A(-2, 4) and B(-4, 2) are reflected in the y-axis. If A' and B' are images of A and B respectively.

(i) Find the co-ordinates of A' and B'.

(ii) Assign a special name to quadrilateral AA'B'B.

(iii) State whether AB' = BA'.

(i) From graph,

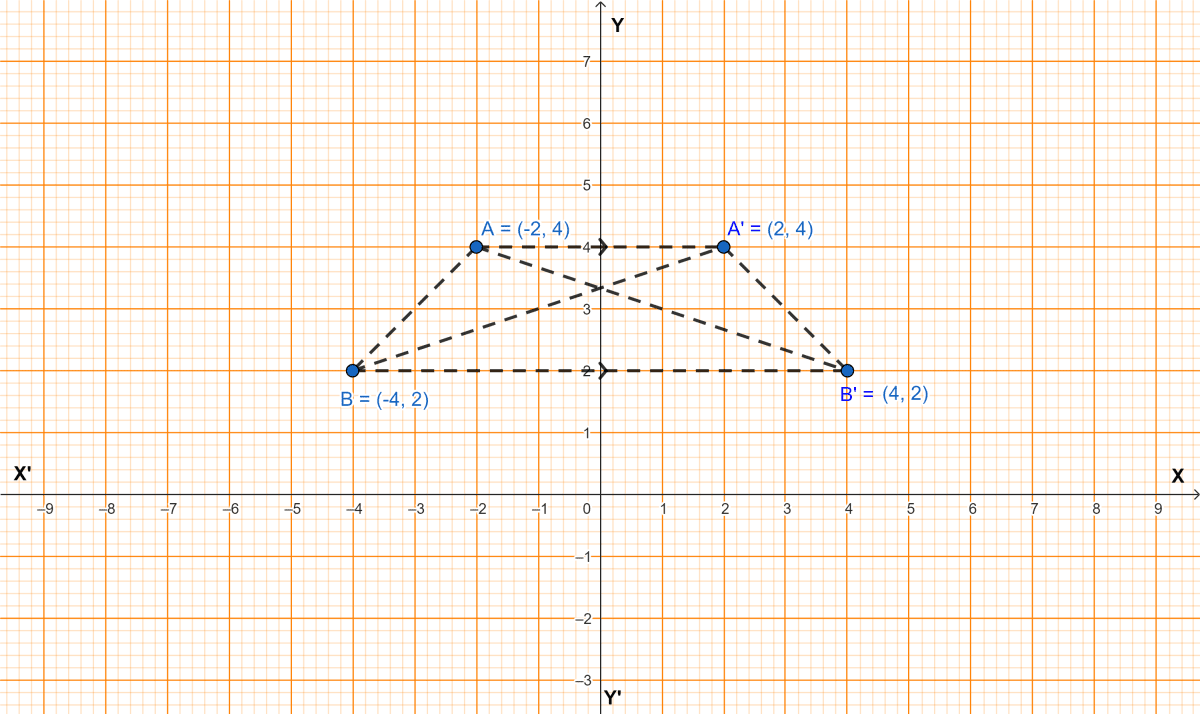
Co-ordinates of A' = (2, 4) and B' = (4, 2).

(ii) By distance formula,

Distance = $\sqrt{(y$2 - y1)^2 + (x2 - x1)^2}

Substituting values we get :

$\text{AB } = \sqrt{(2 - 4)^2 + [-4 - (-2)]^2} \\[1em] = \sqrt{(-2)^2 + [-2]^2} \\[1em] = \sqrt{4 + 4} \\[1em] = \sqrt{8} \\[1em] = 2\sqrt{2}. \\[1em] \text{A}'\text{B}' = \sqrt{(2 - 4)^2 + (4 - 2)^2} \\[1em] = \sqrt{(-2)^2 + 2^2} \\[1em] =\sqrt{4 + 4} \\[1em] = \sqrt{8} \\[1em] = 2\sqrt{2}.$

Since, non-parallel sides are equal.

Hence, AA'B'B is an isosceles trapezium.

(iii) We know that,

In isosceles trapezium diagonals are equal.

Hence, AB' = BA'.