Mathematics
AB and CD are two equal chords of a circle with center O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD; show that OMPN is a square.
Answer
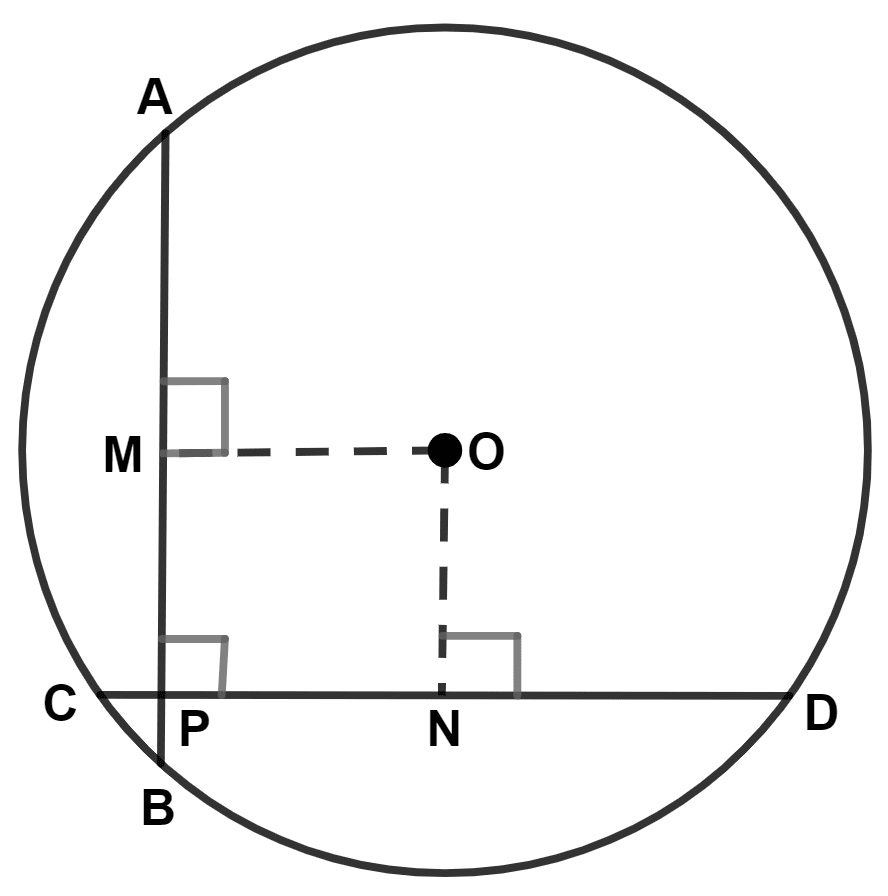
Since, OM ⊥ AB and ON ⊥ CD.
∴ ∠OMP = ∠ONP = 90°.
Given,
AB and CD intersect at right angle.
∴ ∠MPN = 90°.
We know that,
Sum of angles of quadrilateral equal to 360°.
∴ ∠OMP + ∠ONP + ∠MPN + ∠MON = 360°
⇒ 90° + 90° + 90° + ∠MON = 360°
⇒ 270° + ∠MON = 360°
⇒ ∠MON = 360° - 270° = 90°.
Given,
AB = CD
We know that,
Equal chords are equidistant from the center.
∴ OM = ON = x (let) …………(1)
Since,
⇒ AB ⊥ CD and ON ⊥ CD
∴ AB || ON
∴ MP || ON.
⇒ OM ⊥ AB and CD ⊥ AB
∴ OM || CD
∴ OM || PN.
Since, in quadrilateral OMPN opposite sides are parallel.
∴ OMPN is parallelogram.
We know that,
Opposite sides of parallelogram are equal.
∴ MP = ON = x and OM = PN = x
∴ MP = ON = OM = PN.
Since, all sides of quadrilateral OMPN are equal and each interior angle to 90°.
Hence, proved that OMPN is a square.
Related Questions
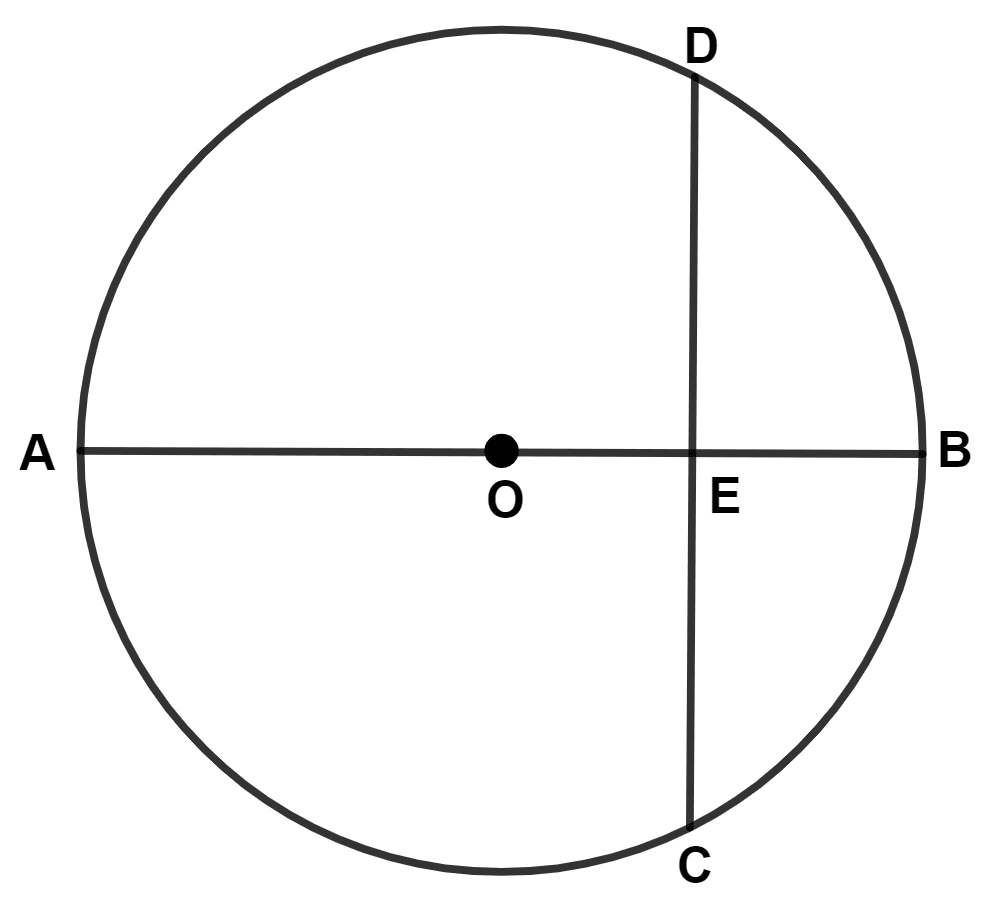
The figure, given below, shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, find the radius of the circle.
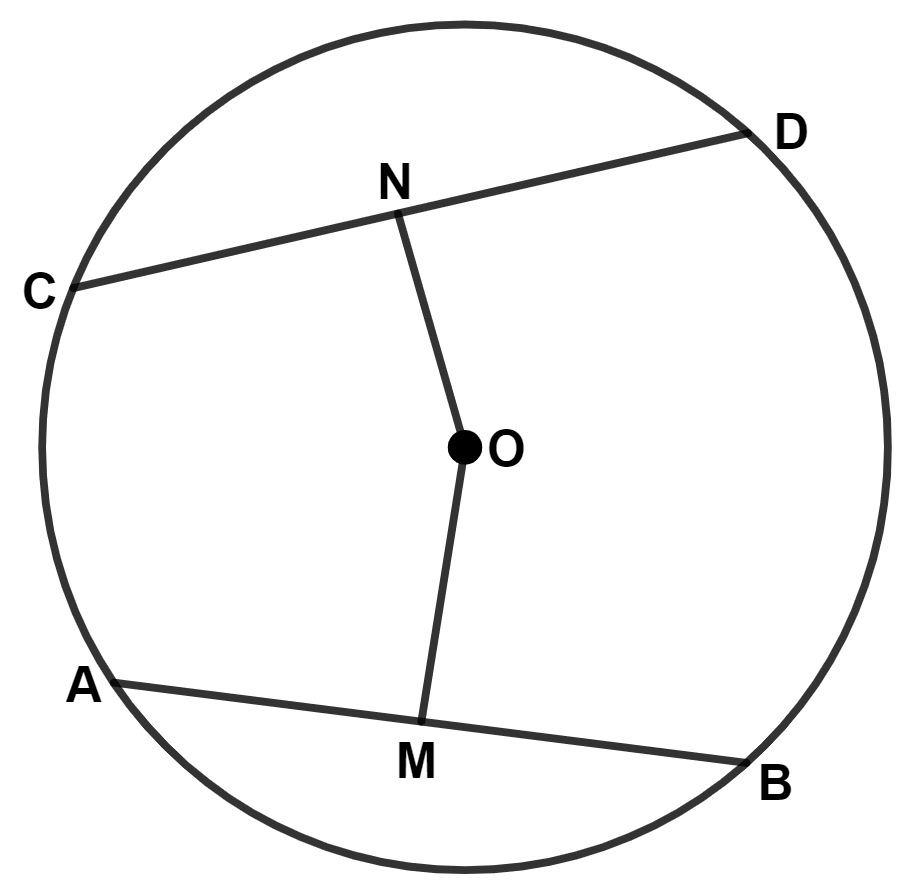
In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) the radius of the circle
(ii) length of chord CD.
The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centers.
Prove that equal chords of congruent circles subtend equal angles at their centers.