Mathematics
AB and CD are the chords of a circle with centre O, ∠AOB = 60° and angles ∠COD = 45°; the ratio between the length of the chords AB and CD is
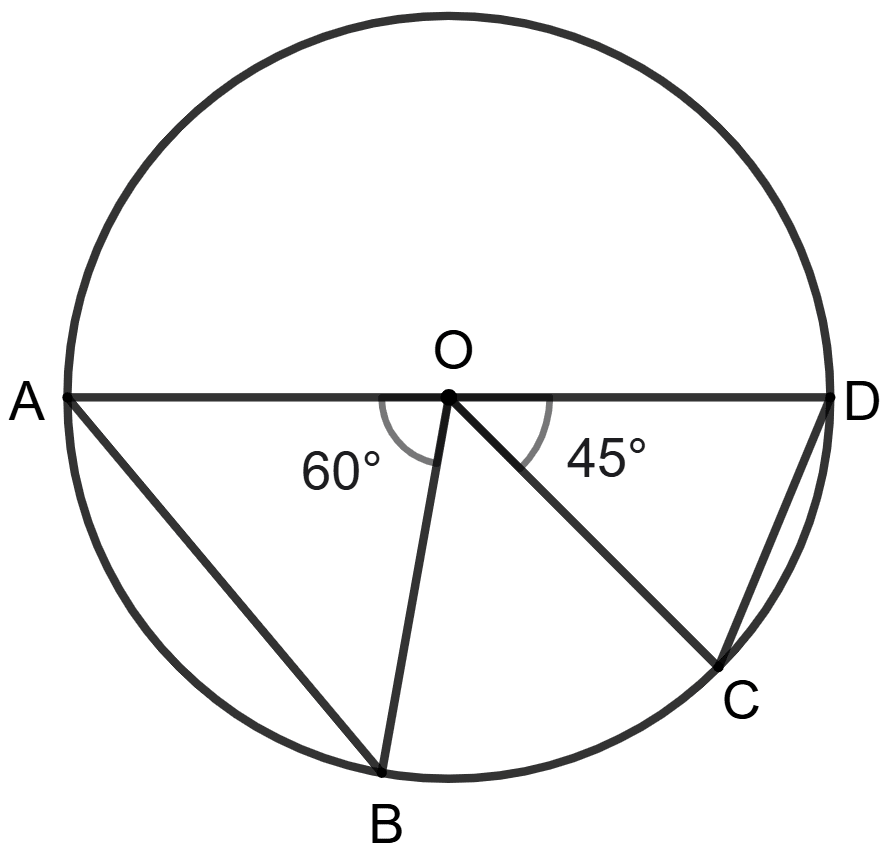
3 : 4
4 : 3
7 : 4
7 : 3
Circles
3 Likes
Answer
We know that,
Ratio of the angles subtended by the chords on the center is equal to the ratio of the length of the chords.
So, ratio between the length of the chords AB and CD is 4 : 3.
Hence, option 2 is the correct option.
Answered By
2 Likes
Related Questions
AB (= 20 cm) is diameter of the given circle and AP (= 16 cm). The distance of chord AP from center O is:
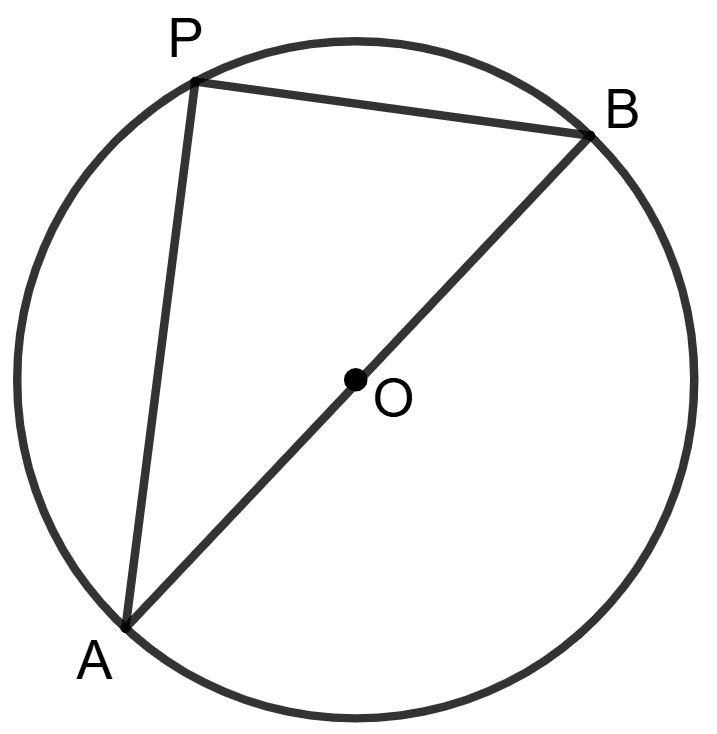
12 cm
18 cm
9 cm
6 cm
Given O is center of the circle with chord AB = 8 cm, OA = 5 cm and OD ⊥ AB. The length of CD is :
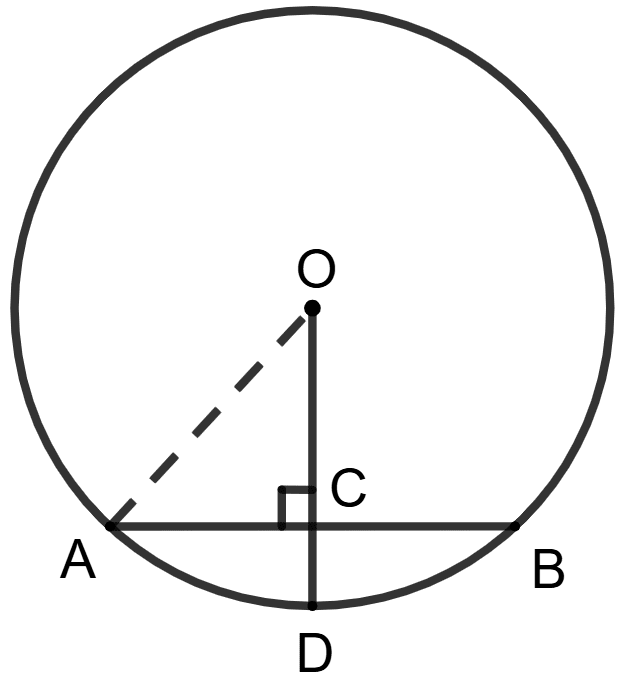
3 cm
5 cm
2 cm
none of these
Statement 1: O and O' are centres of two equal circles and ABCD is a straight line.
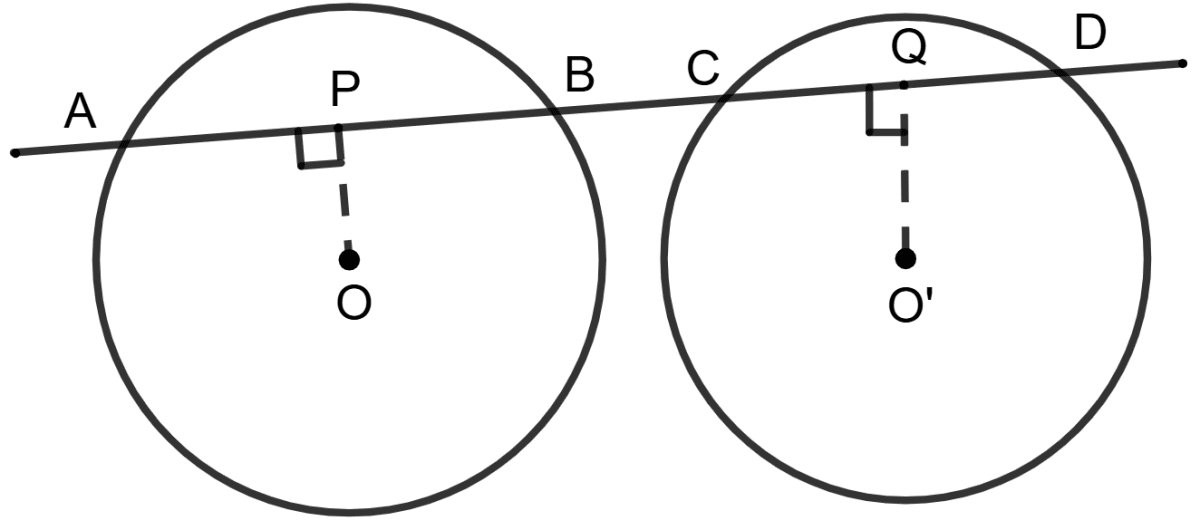
Statement 2: If OP ⊥ AB, O'Q ⊥ CD and O'Q is greater than OP, then CD > AB.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: In a circle with center O, chord AB : chord BC = 1 : 3. If angle AOC is 160° ⇒ angle BOC = 120°.
Statement 2: AB : BC = 1 : 3
⇒ ∠AOC = 3 x ∠AOB
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.