Mathematics
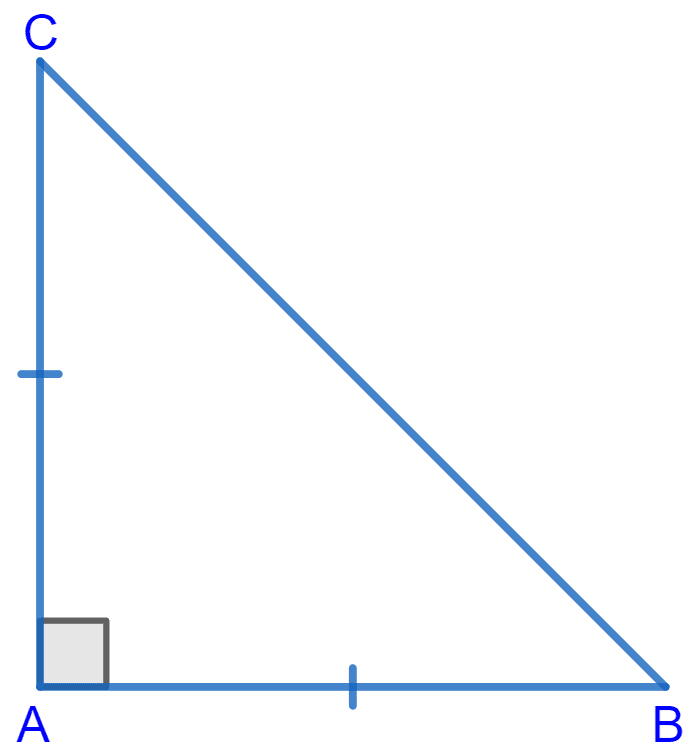
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Triangles
44 Likes
Answer
Given :
AB = AC and ∠A = 90°
We know that,
Angles opposite to equal sides are also equal.
∠C = ∠B = x (let)
In Δ ABC,
⇒ ∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
⇒ 90° + ∠B + ∠C = 180°
⇒ 90° + x + x = 180° (From(1))
⇒ 2x = 180° - 90°
⇒ 2x = 90°
⇒ x =
⇒ x = 45°.
∴ ∠B = ∠C = 45°
Hence, ∠B = 45° and ∠C = 45°.
Answered By
31 Likes
Related Questions
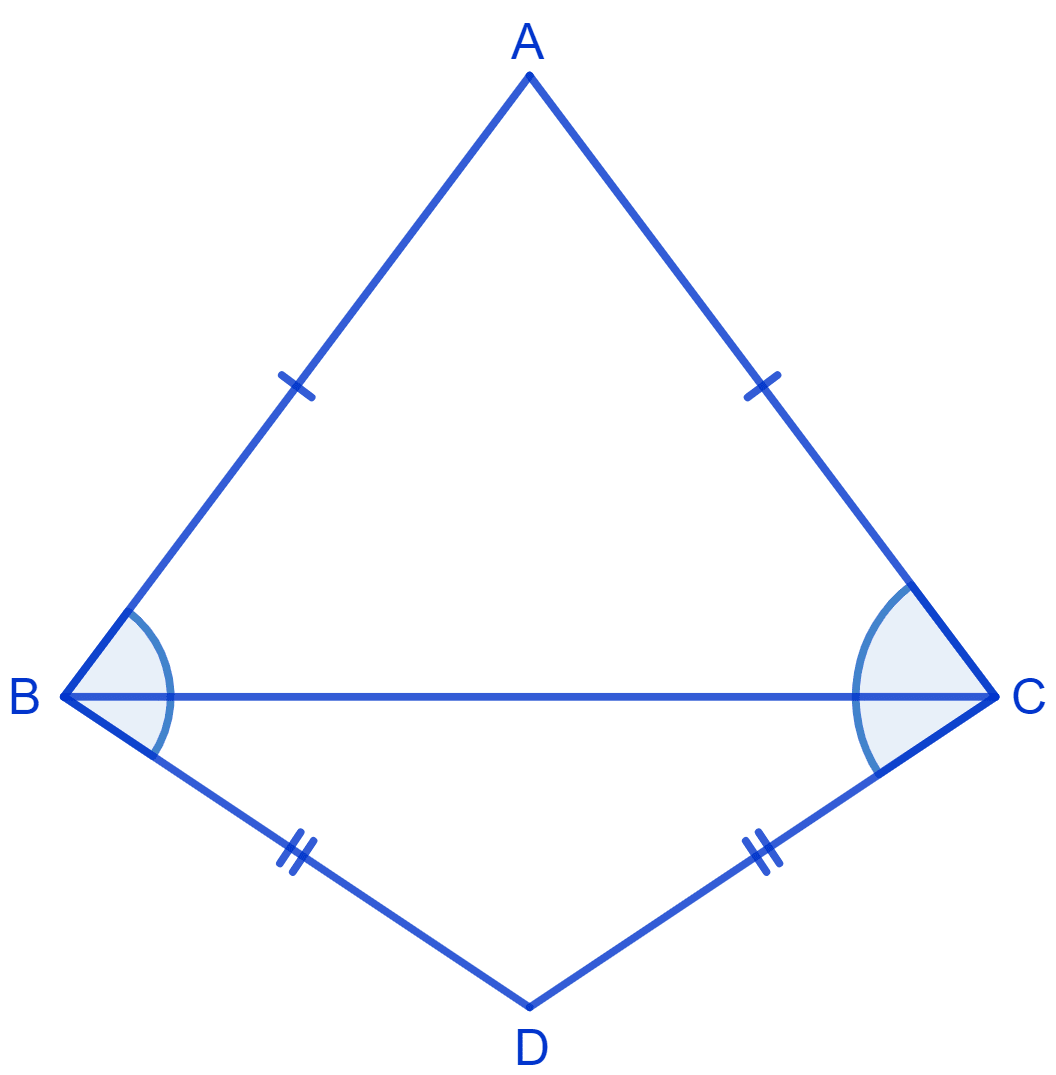
ABC and DBC are two isosceles triangles on the same base BC. Show that ∠ABD = ∠ACD.
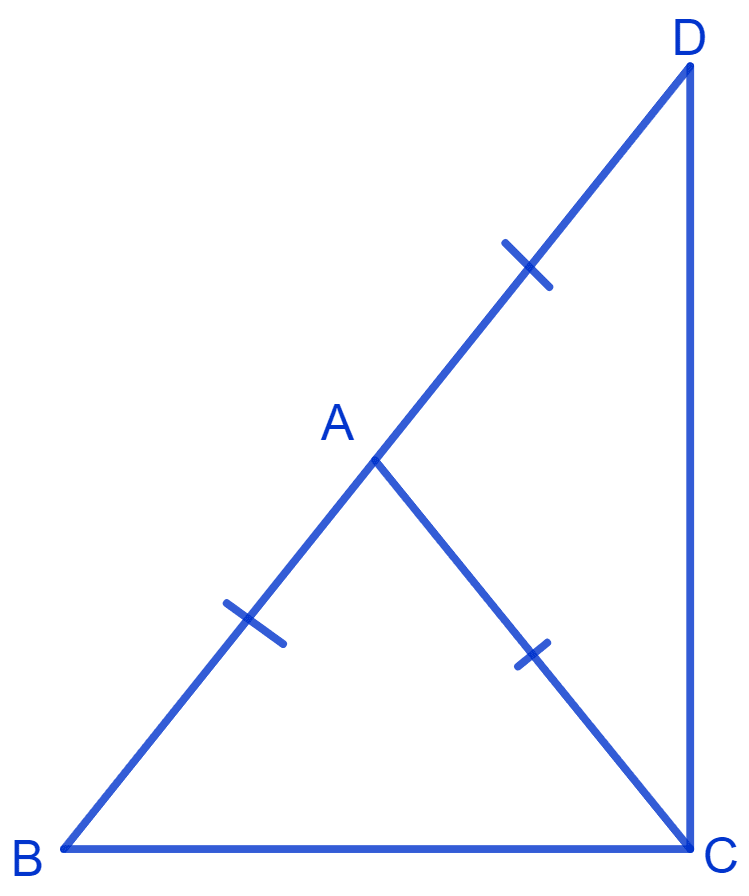
Δ ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that ∠BCD is a right angle.
Show that the angles of an equilateral triangle are 60° each.
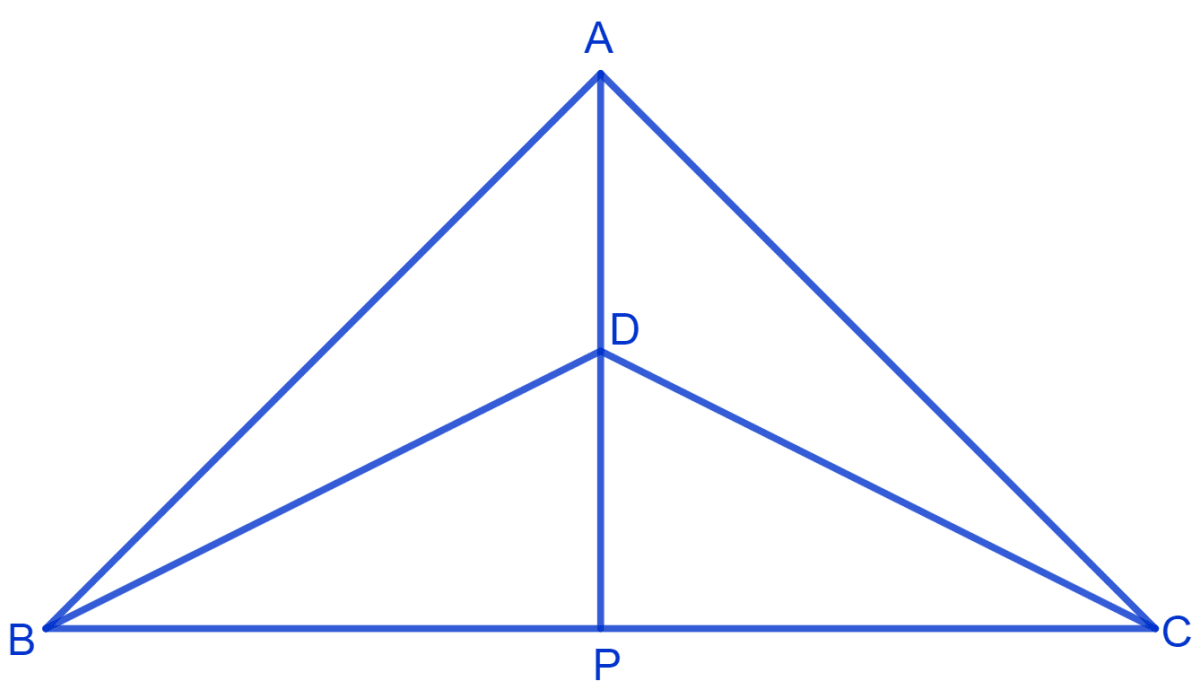
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC